9. Приклад розрахунку

Вихідні дані:

Розрахувати та законструювати середню балку монолітного залізобетонного акведука згідно наступних вихідних даних:

1. Довжина акведука L = 30 м.

2. Ширина акведука В = n х l_s = 2 х 1,8 = 3,6 м.

3. Глибина водяного потоку h_w = 1,6 м.

4. Бетон конструкцій класу В20.

5. Арматура: поздовжня – класу А400, поперечна – класу Вр-І, армування балки виконується зварними каркасами.

9. 1. Компонування акведука

Товщину плити лотока h_s приймають виходячи із умов:

см,

см,

см.

Приймаємо h_s = 12 см.

Висоту стінок лотока приймаємо 1,8 м, що на 20 см вище за рівень води. У місцях з‘єднання дна та стінок лотока влаштовуємо скоси (вути) висотою 10 см під кутом 45⁰ (див. рис. 9.1).

Приймаємо c = l_b / l_c = 0,4, а кількість балок n_b = 5, тоді проліт балки акведука визначаємо за формулою (5)

м.

Виліт консолі визначаємо за формулою (6)

м.

Висоту балки приймаємо в межах h_b = (1/10…1/15)·l_b = = (1/10…1/15)·5,2 = 0,52…0,35 м, остаточно приймаємо h_b = 0,4 м.

Ширину балки приймаємо в межах b_b = (0,3…0,5)·h_b = = (0,3…0,5)·0,4 = 0,12…0,2 м, остаточно приймаємо b_b = 0,18 м.

Згідно отриманих даних будується поздовжніх та поперечних перерізи акведука (див. рис. 9.1 та 9.2).

Рис. 9.1. Поздовжній переріз акведука

Рис. 9.2. Поперечний переріз 1-1

2. Визначення навантажень, що діють на балку

Навантаження на середню балки збираємо з вантажної площі шириною l_s = 1,8 м.

Граничне розрахункове значення постійного навантаження

• від ваги дна лотока:

= (25 · 0,12 · 1,1 + 18 ·0,015 · 0,13) ·1,8 = 6,57 кН/м,

• від власної ваги балки:

= 25 · (0,4 – 0,12) · 0,18 · 1,1 = 1,397 кН/м,

Граничне розрахункове значення тимчасового навантаження від тиску води визначаємо за формулою:

кН/м.

Повне розрахункове граничне значення погонного навантаження на середню балку акведука буде дорівнювати:

= 1,0·1,15·(6,57+1,39+28,8) = 1,0·1,15·(7,96+28,8) = 42,27 кН/м.

3. Статичний розрахунок балки

Розрахунковий проліт балки визначаємо за формулою

м,

а розрахунковий виліт консолі рівний

м.

Розрахункова схема балки акведука являє собою п‘ятипролітну нерозрізну балку з двома консолями, опорами для якої є ригелі проміжних опор, завантажену рівномірно розподіленим навантаженням q_m = 36,76 кН/м (див. рис. 9.3).

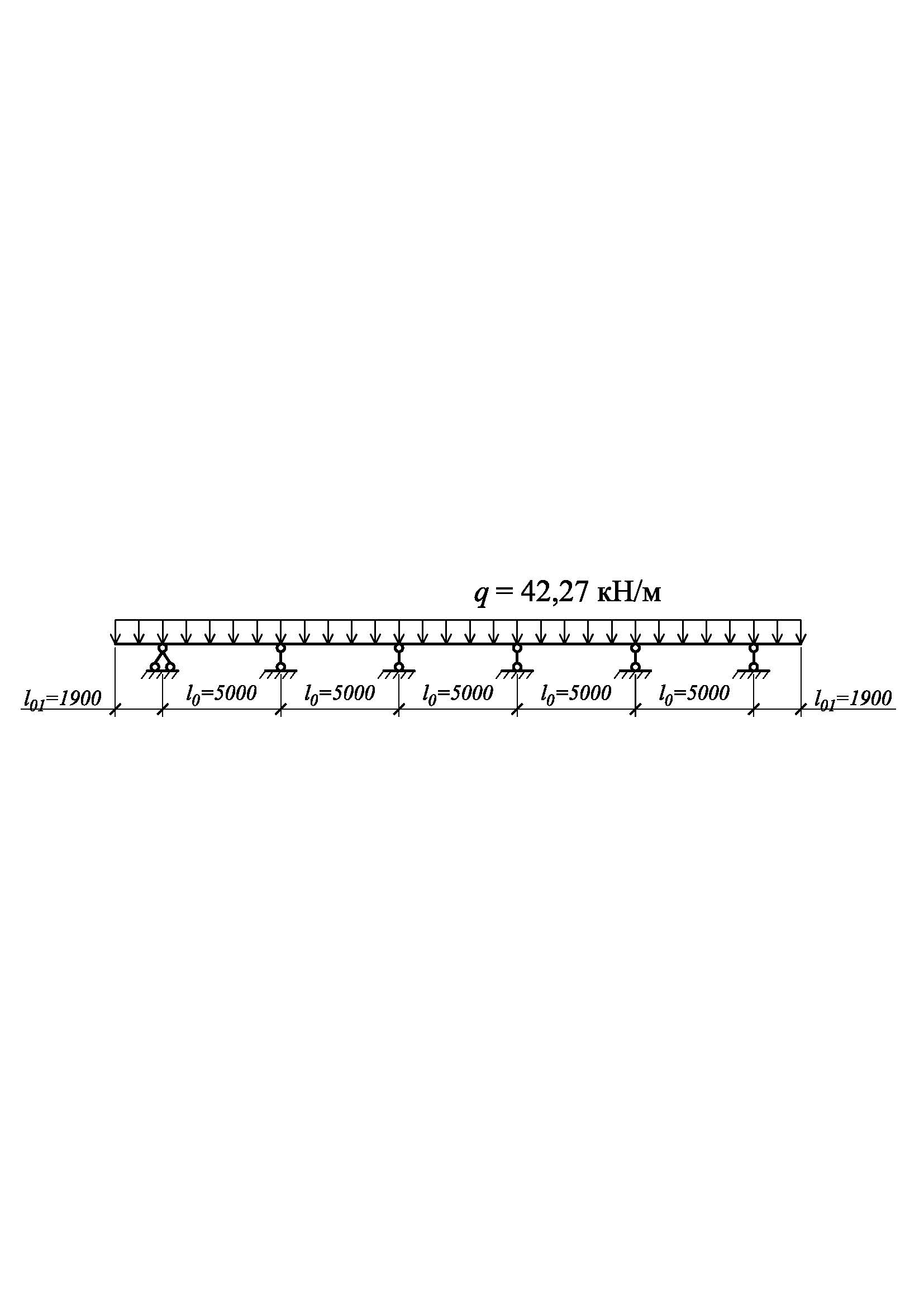
Рис. 9.3. Розрахункова схема балки

Значення згинальних моментів та поперечних сил в балці визначаємо за допомогою табличних коефіцієнтів, наведених в додатку Б.

Дію навантаження на консолі замінюємо згинальним моментом:

кНм.

Опорні моменти від дії консольних моментів:

кНм,

кНм,

кНм.

Опорні моменти від дії рівномірно розподіленого навантаження:

,

кНм,

кНм.

Опорні моменти від дії повного навантаження:

кНм,

кНм,

кНм.

Для визначення прольотних моментів розглядаємо рівновагу однопролітних балок, завантажених рівномірно розподіленим навантаженням та опорними моментами.

Перший проліт

= 102,76 кН

= 108,61 кН.

Координату точки з максимальним моментом визначаємо за формулою (18)

м.

Максимальний момент в першому прольоті:

кНм.

Для більш точної побудови епюри визначаємо моменти через кожні 0,2·l₀ = 0,2·5,0 = 1,0 м від лівої опори:

х₀₁ = 1,0 м кНм;

х₀₂ = 2,0 м кНм;

х₀₃ = 3,0 м кНм;

х₀₄ = 4,0 м кНм.

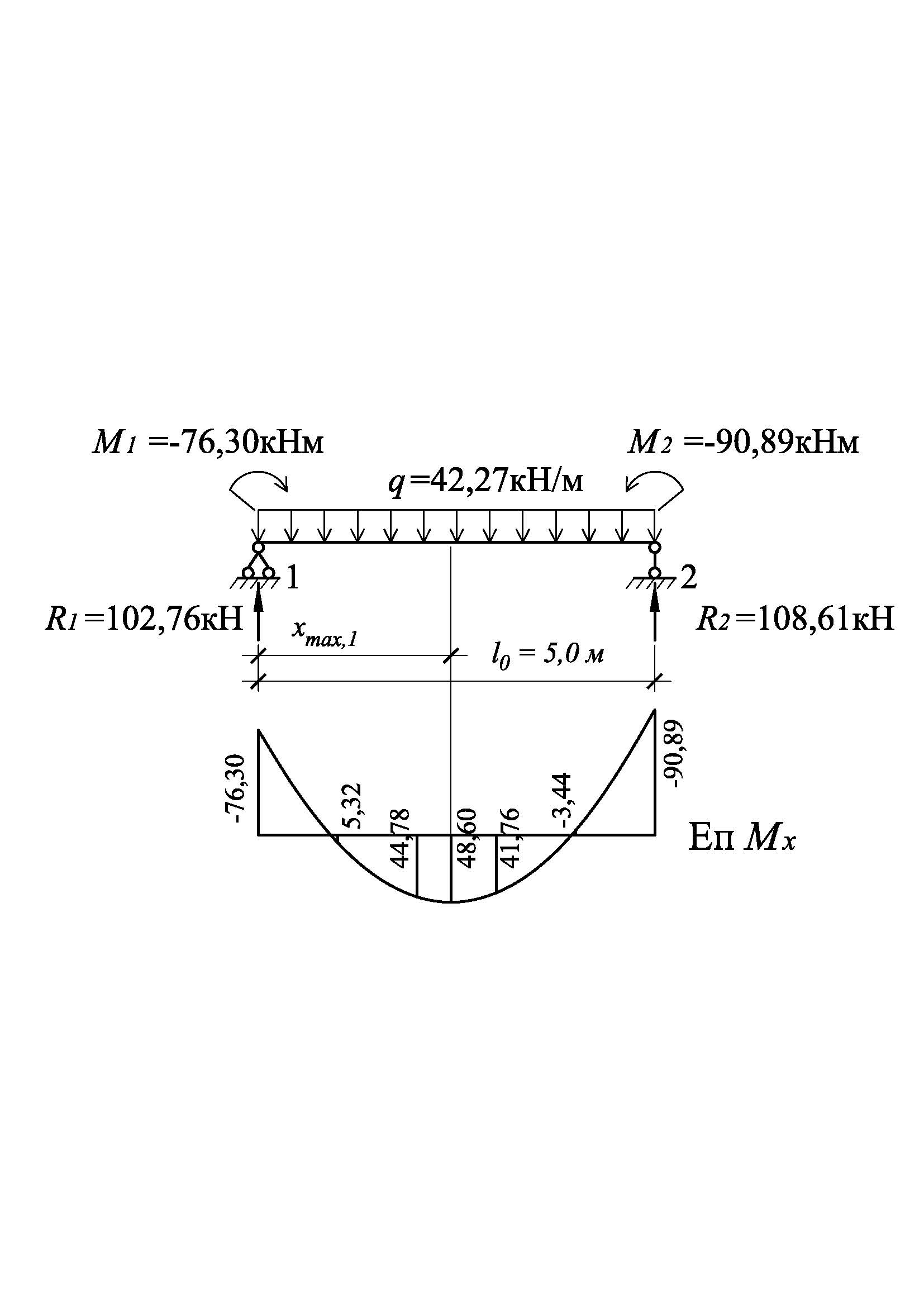
Рис. 9.4. Визначення згинальних моментів в першому прольоті

Аналогічні обчислення виконуємо для решти прольотів.

Другий проліт¹

R`₂ = 106,18 кН, R₃ = 105,19 кН,

х_max,2 = 2,59 м М_2-3 = 42,32 кНм,

М₀₁ = -5,85 кНм, М₀₂ = 36,91 кНм, М₀₃ = 37,41 кНм, М₀₄ = -4,37 кНм.

Третій проліт

R`₃ = 105,68 кН, R₄ = 105,68 кН,

х_max,3 = 2,5 м М_3-4 = 44,65 кНм,

М₀₁ = -2,90 кНм, М₀₂ = 39,38 кНм, М₀₃ = 39,38 кНм, М₀₄ = -2,90 кНм.

Консоль

В консолі згинальні моменти визначаємо через кожні 0,2·l₀₁ = = 0,2·1,9 = 0,38 м:

х_с1 = 0,38 м кНм;

х_с2 = 0,76 м кНм;

х_с3 = 1,14 м кНм;

х_с4 = 1,52 м кНм.

М_с = -76,30 кНм.

Поперечна сила на кінці консолі рівна:

кН.

Будуємо кінцеву епюру згинальних моментів та поперечних сил в середній балці.

Рис. 9.5. Епюри згинальних моментів та поперечних сил