11. Расчет дифр. Картины амплитудно графиче­скими метод.

Д ифракционную задачу можно решить пользуясь а-г методом. Воспользуемся понятием о векторе амплитуды. Это вектор a , длина которого равна амплитуде а, а угол , который вектор составляет с осью ОХ, соответствует начальной фазе данного колебания. при сложении нескольких колебаний движений, изображаемых с помощью векторов a₁, a₂, a₃ с начальными фазами ₁, ₂, ₃, результирующий вектор будет равен векторной сумме векторов, причем угол  между ОХ и рез. вектором определит начальную фазу рез. колебания.

Рассмотрим колебания, приходя­щие в точку наблюдения от каждой зоны. Они имеют амплитуды a_i. Выберем ось ОХ и отложим на ней все эти вектора, приняв фазу а₁ равной 0. Каждый следующий вектор будет короче предыдущего и будет составлять больший угол с ОХ. Суммарное колебание в точке Р изобразится вектором а, соединяющем точку О с концом вектора, соответствующим колебанию, приходящему от последней открытой зоны. Разобьем волновую поверхность на узкие кольцевые зоны таким образом, чтобы колебания, приходящие в точку наблюдения от первой зоны а₁ и от последней a_i имели противоположное направление.

А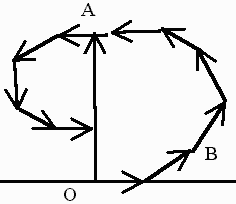 мплитуда рез. колеб. определится вектором ОА. А так как фаза колебания вектора a₁ отличается от фазы колебания a_i yна , то вектор ОА определяет действие, эквивалентное действию первой зоны Френеля. Чтобы учесть действие, эквивалентное действию второй зоны Ф, необходимо достроить эту ломаную еще от 6 следующих зон. Если зоны выбирать бесконечно малыми, то ломаная в пределе перейдет в плавную спираль, с центром в середине вектора ОА и будет аналогична действию открытой волновой поверхности.

Таким образом, а-г метод расчета дифракционной картины приводит к результатам, аналогичным расчету зон по методу Френеля.

12. Дифракция на одной и n щелях.

1 ) На щель шириной а падает параллельный пучок лучей, в фокальной плоскости линзы расположен экран для наблюдения дифракционной картины.

 = 2··(/), где  - оптическая разность хода. =a·sin(),  = (2·(/))·a·sin 

Главный max: sin()=/a, глав­ные min: a·sin()=k· (нечентное число зон Ф на АВ). Относительные max: a·sin()=(2·k+1)·(/2) (четное число зон Френеля).

Интенсивность света, прошед. через щель: I=I₀·(sin²U/ U²), где U= (·a·sin())/.

2 ) Дифракция от многих щелей. Рассмотрим несколько параллельных друг другу щелей ширины а, расположенных на расстоянии b. Интерферируют N пучков, т.к. N щелей. Оптическая разность хода между двумя аналогичными лучами от двух соседних щелей -=(a + b)·sin() =2··(/); max: =2··k, k=0,1,2,3… или (a+b)·sin()=k·; главн.min: a·sin()=k·, k=1,2,3,… побочн. min: (a + b)·sin()=((k·)/N), k=N,2N,3N, …

13. Дифракционная решетка и ее параметры.

С истема, объединяющая N щелей шириной a, разделенных промежутками шириной b называют дифракционной решеткой. d =a+b называют постоянной решетки. В настоящее время Д. Р. имеют 5000 щелей/мм. Существуют реплики с Д.Р.. Они имеют не очень высокое качество и применяются обычно в образовательных целях. Спектр, поученный в результате прохождения света через Д.Р. имеет следующую структуру:

Расстояния между спек­трами соседних порядков с увеличением номера порядка уменьшаются, и спектры начиная с k=2 как правило перекрываются. Для характе-ристики Д. спектров использу-ют следующие параметры: 1. D - угловая дисперсия. 2. D­_L - линейная дисперсия 3. r - разрешающая способность.

1. D=d/d - быстрота изменения Д. угла при изменении длины волны. Величину угловой дисперсии можно определить из условия d·sin()=k·тогда d·cos()d=k·d, D=k/(d·cos()). Для малых  cos~1 и D=k/d. Чем выше порядок спектра, тем больше угловая дисперсия прибора. Вблизи 0 угловая дисперсия сохраняет пост. значение., то есть при этом условии меняется пропорц. .

2. Линейной дисперсией наз. величина равная D=dl/d, где dl - ширина Д. линии на экране.

dlf·d,D_L=f·D

3. r=, где __. В качестве критерия разрешимости спектральных линий лежит критерий Реллея: ₁ и ₂ - разрешимы, если a<=0,8A.

О кончательно: r=k·N (k - число наблюдаемых максиму­мов, N=1/d). Существует способ искусственного уменьшения постоянной решетки: поставить ее под углом к падающему свету.

Тогда d'=dcos'.