4. Когерентные источники света, способы их получения.

Рассмотрим интерференцию света от двух когерентных источ­ников света и классические способы их получения.

В связи с особенностями процесса излучения света возбужден­ными атомами два когерентных источника света получаются на прак­тике из одного и того же источника света. Так как время излучения отдельного атома  ~ 10^-8 с , то за это время свет может распростра­ниться на расстояние S = с·~ 3м . Следовательно, образуется последо­вательность волн, имеющая длину несколько метров. Последующие излучения атома будут происходить в самой произвольной фазе по от­ношению к предыдущему излучению. Поэтому условие когерентности, связанное с постоянством во времени разности фаз, соблюдается лишь в пределах данного расстояния. Это накладывает дополнительные ус­ловия на возможность получения когерентных источников света. Рас­смотрим некоторые способы получения когерентных источников све­та.

1 . Метод Юнга. Метод щелей — один из первых способов наблюдения интерфе­ренционной картины.

Источниками света являются ярко освещенная щель, от которой световая волна падает на две узкие щели S₁ и S₂ освещаемые различ­ными участками одной и той же волны. По принципу Гюйгенса каждая точка волновой поверхности является источником вто­ричных волн. Точки S₁ и S₂ принадлежат одной волновой поверхно­сти, то есть колеблются в одной фазе и, таким образом, являются коге­рентными источниками света. При методе Юнга апертура интерфе­ренции (угол, под которым наблюдается интерференционная картина на экране) 2 = S₁SS₂ определяется отношением расстояний S₂S₁ и SВ, причем расстояние S₁S₂ должно быть много больше ширины ще­лей S₁ и S₂. Таким образом, метод Юнга позволяет получить два дей­ствительных когерентных источника света.

2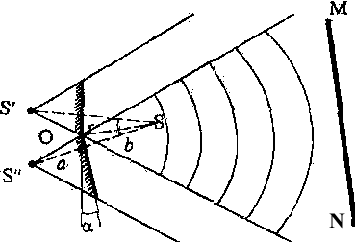 .Бизеркала Френеля. Два плоских соприкасающихся зеркала ОА и 0В рас­положены под углом, близким к 180°, следовательно, . очень мал. Источник света S располагается на расстоянии r парал­лельно линии пересечения зеркал.

Построим изображение источника S в обоих зеркалах, пользу­ясь законами геометрической оптики. Полученные мнимые изображе­ния являются мнимыми когерентными источниками света. Зона пере­крытия волн от этих источников представляет собой зону интерферен­ции. На экране MN, помещенном в эту зону, будет наблюдаться ин­терференционная картина в виде чередующихся темных и светлых по­лос.

Расстояние между источниками света d=2·r·sin(·r·d. расстояние от источников света до экрана l=r+b, а a=r·cos(r, и тогда ширина интерференционной полосы равна x= _· ((r+b) / (2·r·Протяженность области интерференции MN определится выражением 2·b·tg(·b·. Число наблюдаемых интерфереционных полос равно N=(2·b·)/(x).

3 .Бипризма Френеля. Устройство состоит из двух призм с малым преломляющим уг­лом, склеенных по малому основанию. Прямолинейный ис­точник света S располагается параллельно основанию на расстоянии а от призмы. Призма с малым преломляющим углом  обладает сле­дующим свойством: при малом угле падения такая призма отклоняет все лучи на один угол =(n-1), где - преломляющий угол бипризмы; n – коэффициент преломления стекла призмы.

В результате две призмы с малым преломляющим углом обра­зуют две когерентные световые волны, источником которых являются два мнимых источника света S' и S". Расстояние между источниками света d равно d =2·a·sin()2·a·=2·a··(n-1). Тогда ширина интерфер. полосы равна x=((a+b)/(2·a··(n-1)))·_

О бласть интерф. имеет протяженность 2·b·tg()=2·b··(n-1), и число наблюдаемых полос опреде. выражением (3.1). Приведенный выше метод часто применяется на практике для определения неизвестной длины волны  по измеренным x, a и b.

4 .Метод Ллойида. Свет от источника света S (освещен­ной щели) падает под углом, близким к 90°, на плоское зеркало S' - мнимое изображение источ­ника света. На участке MN эк­рана, где перекрываются прямой и отраженный свет, наблюдаются по­лосы интерференции. Особен­ностью данного метода является то, что в центре картины наблюдается темная полоса из-за потери полудлины волны при отражении от зеркала. Т.o. в данном методе получа­ется один действительный и один мнимый когерентные источ­ники света.

5. Билинза Бийе. Собирательная линза разрезается пополам, раздвига­ется на некоторое расстояние, закрытое непрозрачным экраном. От протяженного источника света S, параллельного плоскости разреза, свет падает н а билинзу. В фокальной плоскости линзы на пе­ресечении лучей получаются действительные источники света S₁ и S₂. Зона интерференции MN получается в результате пересечения двух световых пучков от S₁ и S₂.