21. Элементарная теория дисперсии света.

Э/м теория Максвелла сумела объяснить явление интерференции, дифракции, поляризации, но явление дисперсии света она не объяснила. Под явлением дисперсии света понимаются те физические явления, которые обусловлены зависимостью коэф. преломления вещества от длины волны падающего света.

Так как в основном рассматривается граница раздела вакуум – вещество, то речь идет о зависимости абсолютного коэф. преломления вещества от длины волны падающего света

Д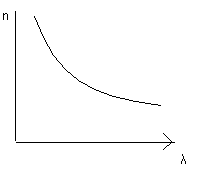 ля характеристики оптических свойств вещества вводится величина, получившая название дисперсия вещества – ν – быстрота изменения коэф. преломления от длины волны ν=Δn/Δλ; ν=dn/dλ из n=f(λ) следует ν=df/dλ=f ’(λ).

λ=f ’(λ).

Для большинства веществ dn/dλ<0 – нормальная дисперсия, но при исследовании цианида было установлено: участки AB, CD – dn/dλ<0 – нормальная дисперсия, участок BC – dn/dλ>0 – аномальная дисперсия.

П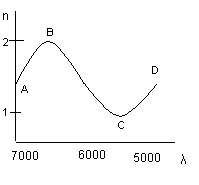 ервым исследователем дисперсии был Ньютон, который пропустил луч света через стеклянную призму и получил окрашенную цветовую полоску, которую назвал спектром (цвета КОЖЗГСФ, у дифракционного спектра – ФСГЗЖОК). При попытке исследовать дисперсию, Коши представил зависимость n в виде ряда n = A+B/n²+C/n³+…; dn/dλ = –2B/n³.

Групповая скорость света. y=a·cos ω(t–r/v) - уравнение гармонических колебаний света в вакууме: r – расстояние от источника волн до точки среды (определяет положение волнового фронта), v – скорость распространения колебаний в данной среде. v = ω/k, k = 2π/λ.

Экспериментально было установлено, что перенос энергии связан не с фазовой скоростью, поскольку в данный момент времени невозможно показать, что находится в точке – горб или впадина. Силовые и энергетические проявления волны связаны с т.н. групповой скоростью: n=v–λ·(v/dλ). Групповая скорость может быть как больше фазовой скорости, так и меньше.

а) Если dv/dλ>0, то из v=c/n => dn/dλ<0 => u<v – нормальная дисперсия. б) Если dv/dλ<0 => dn/dλ>0 => u>v – аномальная дисперсия. в) Если dv/dλ=0 => dn/dλ=0 => u=v – нет дисперсии.

Понятие групповой скорости относится к немонохроматическим колебаниям. Это сложное колебание, которое может быть представлено рядом Фурье как сумма гармонических колебаний. В этом случае под групповой скоростью понимается скорость перемещения сложного максимума немонохроматических колебаний.

Групповая скорость имеет физический смысл только в области нормальной дисперсии.

Элементарная теория дисперсии света. Задача любой теории – дать объяснение экспериментальным фактам и в нашем случае дать объяснение дисперсионной кривой и явлениям нормальной и аномальной дисперсии. Лоренц объяснил явление как результат взаимодействия э/м волны с атомами вещества. Под действием светового вектора волны атомы совершают вынужденные колебания и при этом испускают вторичные волны. Вторичные волны являются когерентными и могут интерферировать как между собой, так и с падающей первичной волной. Результат этой интерференции представляет собой преломленную волну, скорость распределения которой зависит от соотношения амплитуд и начальных фаз интерферирующих волн. v=c/n, n=sqrt(ε_∞·μ)≈sqrt(ε_∞) при ν~10¹⁵ Гц. На этих частотах дипольные моменты не успевают переориентироваться и возникает только электронная поляризация, связанная с воздействием светового вектора волны на атомы вещества.

В соответствии с атомной теорией вещества

E = E₀ cos ωt

Электроны смещаются под действием вектора Е. P_i = –e·x – индуцированный момент.

n² = 1+κ, где κ – диэлектрическая восприимчивость вещества; P_e = n₀κE; κ = P_e/(n₀E);

n^2 = 1+P_e/(n₀E); P_e = n₀P_i = – n₀e·x; n^2=1–e·x/E.

Теория Лоренца предполагала, что электрон в атоме удерживается квазиупрпугой силой F=mv^2/r=m(ω₀^2)r, где ω₀ – собственная частота электрона в атоме.

Если на вещество падает свет с частотой ω, то в результате взаимодействия светового вектора на электроны вещества, они начинают колебаться с частотой падающего света.

F= –kx (квазиупругая); F=eE= E₀ cos ωt

m(ddx/(dtdt))= –kx – eE; k= mω₀²

x= –(eE/m)(1/( ω₀² – ω²)); n² = 1+(e²/m)(1/( ω₀² – ω²))

при ω–>ω₀–0 n–>∞

при ω–>ω₀+0 n–>–∞

ω₀ физического смысла не имеет.

Мы рассмотрели идеальный случай и не учитывали потерю энергии атомами на излучение энергии, соударения и т.п. Эту поправку можно внести, используя силу сопротивления.

F= –rv = –r(dx/dt); 2β = r/m

ddx/(dtdt) + 2β(dx/dt) + (ω₀²)x = –eE

n² = 1+ (n₀(e²)/(2mε₀))·(1/(( ω₀² – ω²)+4(β²)(ω₀²)) (*)

п ри ω = ω₀ к=max (коэф. поглощения). Т.е при частоте, равной собственной частоте колебания электрона в атоме наступает резонансное поглощение энергии в атоме. Т.о. классическая теория дисперсии объяснила ход зависимости коэф. преломления от частоты так. Нормальная дисперсия (монотонный рост n с ростом частоты) объясняется вынужденными колебаниями электронов в атоме под действием э/м волны. Участок аномальной дисперсии объясняется резонансным поглощением энергии атомами вещества, при этом вещество нагревается. Вся предложенная теория учитывает только тот момент, что в атоме находится только один электрон с зарядом e и массой m. В принципе заряд атома может быть различен => существует своя частота атома. А это означает, что в формуле (*) необходимо учесть все колеблющиеся заряды и массы. Получаем серию полос поглощения, соответствующих своей собственной частоте.

Линейчатый спектр дают разреженные газы и пары металлов, полосатый – сложные вещества и молекулы.