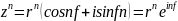14. Вычисление обратной матрицы.

Вычисление обратной матрицы с помощью алгебраических дополнений.

Замечание. Сформулируем еще раз способ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.

Метод гаусса

Матричный метод решения систем линейных уравнений. Систему уравнений можно записать: AX = B. Сделаем следующее преобразование: A^(-1)AX = A^(-1)B, т.к. A^(-1)А = Е, то ЕХ = A^(-1)В Х = A^(-1)В.

К матрице справа приписывается единичная такого же размера, что и исходная: , после чего приводится к виду единичной матрицы методом Гаусса—Жордана; в результате на месте изначальной единичной матрицы справа оказывается обратная к исходной матрица:

15. Ранг матрицы. Способы нахождения.

Рангом матрицы A называется наибольшее целое число r ,что среди определителей порядка r составленных из матрицы А, найдется хотя бы один не равный 0, и все определители порядка r+1 и выше или равны нулю или не могут быть составлены. Способы нахождения: метод элементарных преобразований( привести матрицу к ступенчатому виду). Метод окаймляющих миноров (находим миноры k-го порядка не равные нулю).

16. Линейное векторное пространство.

Линейное, или векторное пространство над полем P - это непустое множество L, на котором введены операции сложения, то есть каждой паре элементов множества ставится в соответствие элемент того же множества, обозначаемый и умножения на скаляр (то есть элемент поля P), то есть любому элементу и любому элементу ставится в соответствие элемент из , обозначаемый .

При этом удовлетворяются следующие условия:

, для любых (коммутативность сложения);

, для любых (ассоциативность сложения);

существует такой элемент , что для любого (существование нейтрального элемента относительно сложения), в частности L не пусто;

для любого существует такой элемент , что (существование противоположного элемента).

(ассоциативность умножения на скаляр);

(умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).

(дистрибутивность умножения на вектор относительно сложения скаляров);

(дистрибутивность умножения на скаляр относительно сложения векторов).

Элементы множества L называют векторами, а элементы поля P - скалярами.

Cⁿ-множество всех n-мерных векторов с введенными операциями и умножением на число, являются линейным пространством, если a_i R, j=1,..,n. Rⁿ-пространство вещественным векторов.

17. Линейная зависимость и независимость векторов.

Говорят, что вектор линейного пространства L линейно выражается через векторы , если его можно представить в виде линейной комбинации этих элементов , т.е. представить в виде .

Определение. Система векторов произвольного линейного пространства линейно независима если из равенства следует равенство нулю всех коэффициентов .Если a_i≠0 то система линейно зависима.

Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.

Теорема. Система векторов произвольного линейного пространства линейно зависима тогда и только тогда, когда хотя бы один вектор системы векторов линейно выражается через остальные векторы системы.

Система векторов называется линейно зависимой (л.з.) если существуют числа , хотя бы одно из которых отлично от нуля, такие что . Если же это равенство возможно только при , то система векторов называется линейно независимой (л.н.з.).

18. Разложение вектора по базису.

Если , то разложение вектора по базису становится суммой слагаемых: В этом случае говорят, что вектор разложен по базису , а числа называются координатами вектора в этом базисе.

19.Ортоганализация базиса.

О.б. называется переход от данного базиса к ортогональному. Процесс Грама-Шмидта:a1,a2,…,an- векторы; e1,e2,…,en – ортогональный базис, который нужно построить.

1. e₁=a₁

2. e₂=a₂-l₂₁e₁; |e₂*e₁|=0=|a₂-l₂₁e₁,e₁|=|a₂,e₁|-l₂₁|e₁,e₁|; l₂₁= 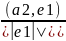; e₂=

3. e₃=a₃-l₂₁e₁-l₃₂e₂; l₃₂= 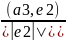; e₃=a₃ - e₁ - e₂

и так далеe.

20. Скалярное произведение в Rⁿ и Сⁿ. Свойства.

Скалярным произведением двух векторов x=(x₁,…,x_n) и y=(y₁,…,y_n) в действительном пространстве Rⁿ(x_iy_i –действительные числа), называется число (x,y)=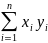

Свойства:

а)  ; при этом равенство нулю имеет место тогда и только тогда, когда ,

б)  ,

в)  .

Скалярным произведением векторов x=( x₁,…,x_n) и y=(y₁,…,y_n) в комплексном пространстве Cⁿ называется число (x,y)=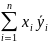

Свойства:

а')  ; при этом равенство нулю имеет место тогда и только тогда, когда ,

б')  ,

в')  .

21.Скалярное произведение в R³. Свойства. Угол между векторами.

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению их длин на косинус угла между ними. Если один из векторов нулевой, то их скалярное произведение равно нулю.

Свойства:

• (a,b)=(b,a)

• a перпендикулярен b если (a,b)=0

• (a,a)=||a||²

• (i,i)=(j,j)=(k,k)=1; (i,j)=(j,i)=(j,k)=(k,j)=0, i,j,k – ортонормированный базис R³

• (a1+a2, b)=(a1,b)+(a2,b)

• (la,b)=(a,lb)=l(a,b), l – числовR³

Угол между векторами в R³ – наименьший укол между aиb, имеющими при этом общее начало. Направление вращения при этом не учитывается.

22. Векторное произведение в R³. Свойства

Векторным произведением axb[a,b] называют такой вектор с, что он перпендикулярен как а, так и b, а его длина равна произведению длин aи bна синус угла между ними.

Свойства:

Если хотя бы один из векторов нулевой или пропорционален другому, их векторное произведение равно нулевому вектору.(т.е. еслиониколлинеарны)

[a,b]=-[b,a]

[I,j]=k; [I,k]=-j; [j,k]=i

[la,b]=[a,lb]=l[a,b]

[a+b,c]=[a,c]+[b,c]

Выражение векторного произведения через декартовы координаты:

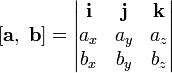
23. Смешанное произведение векторов. Свойства.

Смешанным произведением упорядоченной тройки векторов называется скалярное произведение векторного произведения: ([a,b],c)

Свойства:

1. Для того, чтобы векторы a,b,cлежали в одной плоскости, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.

2. ([a,b],c)=(a,[b,c])

3. Выражением с произведения через координаты вектора: ([a, b],c)=x₃(y₁z₂-y₂z₁)-y₃(x₁z₂-x₂z₁)+z₃(x₁y₂-x₂y)-det , a=(x₁,y₁,z₁); b=(x₂,y₂,z₂); c=(x₃,y₃,z₃)

4. Abc=-bac

5. Abc=cab=bca

24. Уравнение плоскости. Взаимное расположение плоскостей.

Теорема: Всякой плоскости в пространстве, заданной ортогональной системой координат, соответствует уравнение первой ступени, и всякому уравнению первой ступени соответствует некоторая плоскость.

Уравнение плоскости, проходящей через точку (x0,y0,z0) и имеющей нормаль (A,B,C): A(x-x0)+B(y-y0)+C(z-z0)=0

Уравнение плоскости через три точки: |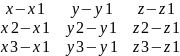 |=0 , где xyz1, xyz2, xyz3 – координаты данных точек.

Уравнение плоскости в отрезках: x/a+y/b+z/c=1, где a,b,c – координаты векторов нормали.

Угол между плоскостями – угол между нормалями этих плоскостей.

25. Уравнение прямой в R³. Уравнение отрезка.

Векторное ур-е прямой:r̅=r̅₀+tS̅, где r– вектор…

Уравнение прямой через две заданные точки: , где xyz1 и xyz2 – координаты заданных точек.

Уравнение отрезка: , отношение длины отрезка к длине прямой.

26. Взаимное расположение прямой и плоскости.

Плоскость: Ax+By+Cz+D=0; нормаль: n̅=[A,B,C];прямая: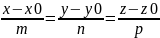 ; напр. вектор: S̅=[m,n,p]

Если прямая параллельна плоскости, то напр. вектор перпендикулярен нормали (их скалярное произведение – ноль): Am+Bn+Cp=0

Если прямая перпендикулярна плоскости, то направляющий вектор параллелен нормали:

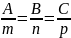
27. Ортогональный базис. Коэффициенты Фурье разложения по базису.

;умножим скалярно на a_k; 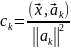-коэффициент Фурье.

28. Неравенство Коши-Буняковского

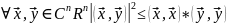
Док: пусть 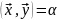, ,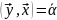 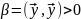; ; 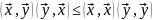чтд.

29.Частные производные. Необходимые условия дифференцируемости в Rⁿ и R.

Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆_хz. Итак,

Δ_хz=ƒ(х+Δх;у)-ƒ(х;у).

Аналогично получаем частное приращение z по у:

Δ_уz=ƒ(x;у+Δу)-ƒ(х;у).

Полное приращение Δz функции z определяется равенством

Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у).

 Если существует предел

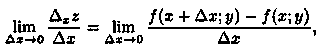
то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов:

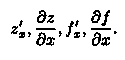
Частные производные по х в точке М₀(х₀;у₀) обычно обозначают символами

Аналогично определяется и обозначается частная производная от z=ƒ(х;у) по переменной у:

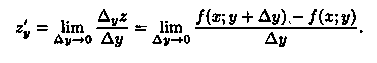
(необходимое условие дифференцируемости). Если функция нескольких переменных f: Rⁿ → R дифференцируема в точке x, то у этой функции в точке x существуют все (конечные) частные производные.

30.Дифференциал ФНП. Достаточные условия дифференцируемости.

(по большей части тоже самое что в предыдущем)

Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆_хz. Итак,

Δ_хz=ƒ(х+Δх;у)-ƒ(х;у).

Аналогично получаем частное приращение z по у:

Δ_уz=ƒ(x;у+Δу)-ƒ(х;у).

Полное приращение Δz функции z определяется равенством

Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у).

 Если существует предел

то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов:

Частные производные по х в точке М₀(х₀;у₀) обычно обозначают символами

Аналогично определяется и обозначается частная производная от z=ƒ(х;у) по переменной у:

(достаточное условие дифференцируемости). Если функция нескольких переменных f: Rⁿ → R в некоторой окрестности точки a определена и имеет частные производные по всем переменным, причем все производные непрерывны в самой точке a, то функция f дифференцируема в точке a.

31.арифмитические действия с комплексными числами, заданными в тригонометрической и показательной форме.

z₁=r₁(cosf₁+isinf₁)= r₁e^if1

z₂=r₂(cosf₂+isinf₂)= r₂e^if2

1)

2)

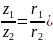
3)