7. Матрицы, действия с матрицами. Операции транспонирования и сопряжения. Матрица — это прямоугольная таблица числе aij (действительных и комплексных) вида

A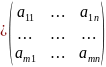 состоящая из m строк и n столбцов. При m=n она называется квадратной матрицей n-го порядка.

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции:

Две матрицы называются равными если у них совпадают размерности и совпадают элементы стоящие при одинаковых местах( a_ij=b_ij)

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен c_ij = a_ij + b_ij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой c_ij = a_ij - b_ij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть .

Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A — матрица размера , то A^T — матрица размера

Свойства операций над матрицами

Ассоциативность сложения: A + (B + C) = (A + B) + C.

Коммутативность сложения: A + B = B + A.

Ассоциативность умножения: A(BC) = (AB)C.

Вообще говоря, умножение матриц не коммутативно: . Используя это свойство, вводят коммутатор матриц.

Дистрибутивность умножения относительно сложения:

A(B + C) = AB + AC;

(B + C)A = BA + CA.

Свойства операции транспонирования матриц:

(A^T)^T = A

(AB)^T = B^TA^T

(A ^{− 1})^T = (A^T) ^{− 1}, если обратная матрица A ^{- 1} существует.

Если элементы матрицы А комплексные числа то матрицу, которую получают из А с помощью транспонирования и замены каждого комплексного числа на сопряженное, называют сопряженной

8. Решение системы линейных алгебраических уравнений методом Гаусса-Жордана.

Суть метода заключается в последовательном исключении неизвестных. Рассмотрим систему линейных уравнений: 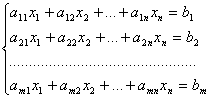Разделим обе части 1–го уравнения на a11 <> 0, затем: 1) умножим на а21 и вычтем из второго уравнения 2) умножим на а31 и вычтем из третьего уравнения и т.д. Получим: 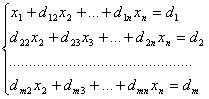, где d1j = a1j/a11, j = 2, 3, …, n+1. dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1. Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.

Допускаются следующие элементарные преобразования:

1)Перестановка строк расширенной матрицы.

2)Умножение i-й строки расширенной матрицы на число альфа, не равное нулю.

3)Прибавление к i-й строке расширенной матрицы j-ю строку умноженную на заданное число альфа.

рассмотрим некоторые ситуации:

( 0 0 0 ... 0 I bi ) - нет решений

две одинаковые строчки. - одну из них можно вычеркнуть.

если в строчке стоят одни нули, то мы её вычёркиваем.

9. Определитель квадратной матрицы. Свойства.

Для каждой квадратной матрицы определено число, называемое определителем матрицы.

Определителем матрицы первого порядка  называется число, равное единственному

элементу этой матрицы: A = {a}, detA = |A| = a.

Пусть A — произвольная квадратная матрица порядка n, n>1:

Определителем квадратной матрицы n-го порядка, n >1, называется число, равное

где M_ij — определитель квадратной матрицы, полученной из матрицы A вычеркиванием

i-й строки и j-го столбца(минор).

Квадратная матрица называется вырожденной, если её определитель равен нулю.

Квадратная матрица называется невырожденной, если её определитель отличен от нуля.

1. Величина определителя не изменится, если его строки и столбцы поменять ролями:

2. При перестановке двух столбцов (строк) определитель меняет знак на противоположный:

3. Общий множитель элементов какой-нибудь строки (какого-нибудь столбца) может быть вынесен за знак определителя:

4. Если все элементы некоторого столбца (некоторой строки) равны нулю, то сам определитель равен нулю:

5. Если элементы двух столбцов (строк) определителя пропорциональны, то определитель равен нулю:

Следствие. Если определитель имеет два одинаковых столбца (две одинаковых строки), то он равен нулю:

6. Свойство линейной комбинации параллельных рядов определителя. Определитель не изменится, если к элементам одного столбца (одной строки) прибавить соответствующие элементы другого столбца (другой строки), умноженные на одно и то же число.

7. Определитель равен сумме произведений элементов любой его строки (либо его столбца) на их алгебраические дополнения.

8. Сумма произведений элементов какой-нибудь строки (какого-нибудь столбца) на алгебраические дополнения другой строки (другого столбца) равна нулю.

10. Теорема Крамера (док - во).

Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам: x_i = _i/, где  = det A, а _i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i. _i =

док-во: Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

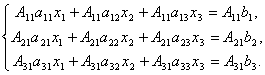
Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца:

Далее рассмотрим коэффициенты при x₂: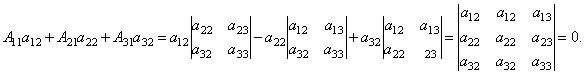

Аналогично можно показать, что и  .

Наконец несложно заметить, что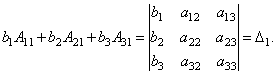 

Таким образом, получаем равенство:  .

Следовательно,  .

Аналогично выводятся равенства   и  , откуда и следует утверждение теоремы.

11. Однородные системы линейных уравнений.

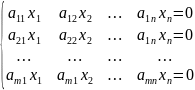;A=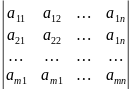 если m=n и detA≠0 ,то система имеет единственное решение(нулевое). Однородная система, в которой m=n имеет не нулевое когда detA=0.

12.Матричные уравнения АX=B и Х*А=В.

AX=B

A=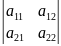 ;X= ; B= ;AX= ;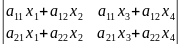

X*A=B; (X*A)^T=A^T *X^T =B^T;

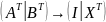
Матрица совместна если имеет хотя бы одно решение, и несовместна если наоборот.

13. Обратная матрица, существование и единственность.

Всякая невырожденная матрица имеет обратную, и при том только одну. Если A^-1*A= A* A^-1=I.

A^-1=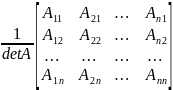

Определение. Квадратная матрица А называется вырожденной, если , и невырожденной, если .

Определение. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если А*В = В*А = Е. При этом В обозначается .

Теорема. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.

Свойства обратных матриц. Укажем следующие свойства обратных матриц: 1) (A^(-1))^(-1) = A; 2) (AB)^(-1) = B^(-1)*A^(-1) 3) (A^(T))^(-1) = (A^(-1))^(T).