
- •1. Комплексные числа: определение, алгебраическая форма записи, действия.
- •2. Геометрическая интерпретация комплексных чисел. Модуль комплексного числа. Комплексное сопряжение и его свойства.
- •3. Тригонометрическая форма записи кч.
- •?Войства модуля и аргумента кч. Ф-лы Муавра. ???
- •7. Матрицы, действия с матрицами. Операции транспонирования и сопряжения. Матрица — это прямоугольная таблица числе aij (действительных и комплексных) вида
- •14. Вычисление обратной матрицы.
- •16. Линейное векторное пространство.
- •17. Линейная зависимость и независимость векторов.
?Войства модуля и аргумента кч. Ф-лы Муавра. ???
Св-ва модуля: Число |z|=(x^2+y^2)^(1/2) называется модулем числа z. Для вещественного числа модуль совпадает с его абсолютной величиной. Некоторые свойства модуля:
|z|>=0, причём |z|=0 тогда и только тогда, когда z=0; |z1+z2|<=|z1|+|z2| (неравенство треугольника); |a*z|=a*|z|, - эти три свойства вводят на комплексных числах структуру двумерного нормированного пространства над полем R;
|z1*z2|=|z1|*|z2|; |z1/z2|=|z1|/|z2|.
Угол f такой, что: cos(f)=x/|z| и sin(f)=y/|z|, называется аргументом z. Для комплексного нуля значение аргумента не определено, для ненулевого числа z аргумент определяется с точностью до 2Пk, где k - любое целое число. Из определения следует, что tg(f)=y/x.
Св-ва аргумента: аргумент произведения равен сумме аргументов, аргумент частного равен разности аргументов, арг(z)^н=н*арг(z), аргумент сопряжённого кч равен отрицательному аргументу кч.
Ф-ла Муавра: Формула Муавра для комплексных чисел z=r*(cos(f)+i*sin(f)), заданная в тригонометрической форме - формула (r(cos(f)+i*sin(f)))^n=r^n*(cos(nf)+i*sin(nf)) для любого n из Z. Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа
Отметим, что корни n-й степени из комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n-угольника, вписанного в окружность радиуса (r)^(1/n) с центром в точке 0.
4. Решение уравнений zn = zo и z2+pz+q=0.
z
называется корнем nй
степени из a
если
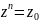 ;
Если
;
Если
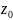 =0,
то при любом n,
ур-е имеет 1 корни(z=0)
=0,
то при любом n,
ур-е имеет 1 корни(z=0)
Если
≠0,
z≠0,
то z=r(cosf+isinf)
, a=ρ(cosθ+isinθ);
zn=rn(cos(nf)+isin(nf))
, zn=a
тогда rn=ρ
и nf=θ+2пk,где
k-
это целые числа. Тогда zk= где k=0,1..n-1.
az2+pz+q=0,
a≠0,
a,b,c
–комплексные числа
где k=0,1..n-1.
az2+pz+q=0,
a≠0,
a,b,c
–комплексные числа

 .
Если
.
Если
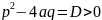 ,
то
,
то
 ,
если D
,
если D

5. Многочлены, основные свойства. Теорема Безу.
Pn(z)=a0zn+a1zn-1+..+an-1z+an –многочлен (полином), n- натуральное число, n- степень многочлена, ai(i=0,1,..,n)- коэффиценты многочлена Pn(z)=0 –нулевой многочлен. Корнем многочлена называется такое значение z0 переменной z, при которой P(z0)=0. Для любых двух многочленов существуют такие многочлены, что P(z)=Q(z)*g(z)+R(z) где P(z)-делимое Q(z)-делитель ,g(z)-частное ,R(z)-остаток.
Теорема Безу: остаток от деления многочлена P(x) на двучлен (x – a) равен P(a).
6.Рациональные дроби. Разложение в сумму простейших.
Рациональной
дробью называется функция вида
 где Q(z)
и P(z)
–многочлены. Если Q
где Q(z)
и P(z)
–многочлены. Если Q P
это правильная Р.д., если
P
это правильная Р.д., если
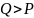 то
неправильная.
то
неправильная.
1) Если дробь неправильная, выделить целую часть, следующие пункты применить к остатку
2) Найти действительные корни знаменателя:
а) Если это многочлен степени 3 и выше, некоторые его корни стоит искать перебором делителей свободного члена.
б) Когда найден хотя бы один корень x1, нужно разделить исходный многочлен на (x - x1).
в) Пункты 1) и 2) нужно повторять до тех пор, пока будет получено квадратное уравнение, корни которого находят по школьным формулам. Если действительных корней нет - оставляют так.
3) Представить знаменатель в виде произведения (x - x1)(x - x2)...
4) Получить сумму дробей, в знаменателе каждой из которых находится один из множителей предыдущего пункта, а в числителе - многочлен степени на 1 меньше, чем в знаменателе. Если некий корень оказался кратным степени m, то ему будет соответствовать m дробей, со знаменателями в степени от 1 до m
5) Привести полученные дроби к общему знаменателю и сложить
6) Приравнять полученную дробь к исходной правильной дроби из пункта 0
7) Приравнять коэффициенты при х в одинаковых степенях справа и слева от знака "="
8) Решить полученную систему уравнений
9) Подставить полученные коэффициенты в соответствующие дроби.
