1. Комплексные числа: определение, алгебраическая форма записи, действия.

Определение: комплексное число z - это упорядоченная пара вещественных чисел (x, y) с введёнными на них следующим образом операциями сложения и умножения: (х, у)+(х’, у’)=(х+х’, у+у’); (х, у)*(х’, у’)=(хх’-уу’, ху’+ух’). Вещественные числа представлены в этой модели парами вида (х, 0), причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Мнимая единица в такой системе представляется парой i=(0, 1).

Алгебраическая форма: z=a+bi, i^2=(-1), где i - мнимая единица; a - действительная часть: a = Re(z); bi - мнимая часть: b = Im(z); числа вида bi - чисто мнимые; плоскость Oxy - комплексная плоскость; ось Ох - действительная ось; ось Oy - мнимая ось;

Действия над комплексными числами: если z1=a+bi, z2=c+di, то:

z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i; z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i; z1=z2 <=> a=c, b=d; z1*z2=(a+bi)*(c+di)=(ac-bd)+(ad+bc)i; z1/z2=(a+bi)/(c+di)=(ac+bd)/(c^2+d^2)+(bc-ad)i/(c^2+d^2); i^4k=1, i^(4k+1)=i, i^(4k+2)=-1, i^(4k+3)=-i.

2. Геометрическая интерпретация комплексных чисел. Модуль комплексного числа. Комплексное сопряжение и его свойства.

Геометрическая интерпретация: рассмотрим на плоскости декартову прямоугольную систему координат xOy. Каждому комплексному числу z=a+bi можно сопоставить точку с координатами (a, b), и каждой точке с координатами (c, d) можно сопоставить комплексное число w=c+di. Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.

Модуль: пусть комплексное число z=a+bi изображается радиус-вектором. Тогда длина этого вектора называется модулем числа z и обозначается |z|. Очевидно, что |z|=(a^2+b^2)^(1/2). Угол, образованный радиус-вектором числа z с осью Ox, называется аргументом числа z и обозначается arg(z). Аргумент числа определяется не однозначно, а с точностью до числа, кратного 2П. Однако, обычно аргумент указывают в диапазоне от 0 до 2П или в диапазоне от –П до П. Кроме того у числа z=0 аргумент не определен. Arg(z) равен углу f. Из того же рисунка очевидно, что tg(f)=b/a. С помощью этого соотношения можно находить аргумент комплексного числа: arg(z)=arctg(b/a) или arg(z)=П+arctg(b/a), причем первая формула действует, если изображение числа z находится в первой или четвертой четверти, а вторая, если во второй или третьей. Если a=0, то комплексное число изображается вектором на оси Oy и его аргумент равен П/2 или 3П/2. Получим еще одну полезную формулу: пусть z=a+bi. Тогда _z=a-bi; z*(_z)=(a+bi)*(a-bi)=a^2+b^2. С учетом формулы получим z*(_z)=|z|^2 или |z|=(z*(_z))^(1/2).

Комплексное сопряжение: если комплексное число z=x+iy, то число 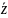=x-iy называется сопряжённым (или комплексно сопряжённым) к z.

Свойства: ;

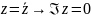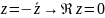
3. Тригонометрическая форма записи кч.

Тригонометрическая форма записи: Пусть z=a+bi. Положим r=|z|, f=arg(z). Очевидно, что a=r*cos(f), b=r*sin(f). Тогда z=r*cos(f)+(r*sin(f))*i. Это выражение запишем в виде z=r*(cos(f)+i*sin(f)). Последняя запись называется тригонометрической формой комплексного числа. В отличие от нее запись числа в виде a+bi называют иногда алгебраической формой комплексного числа. Отметим, что тригонометрическая форма - это указание числа по двум его характеристикам: модулю и аргументу. Замечание: При записи числа в тригонометрической форме НЕЛЬЗЯ вычислять значения cos(f) и sin(f), иначе мы потеряем явное указание аргумента z и снова вернемся к алгебраической форме. Кроме того, если угол f получился отрицательным, то знак "-" НЕЛЬЗЯ выносить за знак синуса и НЕЛЬЗЯ убирать его под знаком косинуса.

Ф-ла Эйлера. Показательная форма записи кч.

Ф-ла Эйлера: Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство: e^(ix)=cos(x)+i*sin(x), где e - основание натурального логарифма, i - мнимая единица.

Док-во: Доказательство формулы Эйлера достаточно тривиально. Разложим функцию e^(ix) в ряд Тейлора по степеням x. Получим: e^(ix)=1+ix/1!+(ix)^2/2!+(ix)^3/3!...=(1-x^2/2!+x^4/4!-x^6/6!+…)+i(x/1!-x^3/3!+x^5/5!-...)

Но (1-x^2/2!+x^4/4!-x^6/6!+…)=cos(x), (x/1!-x^3/3!+x^5/5!-...)=sin(x). Поэтому e^(ix)=cos(x)+i*sin(x).

Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой e^(ix)=cos(x)+i*sin(x), которая носит название формулы Эйлера. Обосновать ее можно с помощью теории степенных рядов. Эта теория будет изложена в курсе математического анализа. Пусть комплексное число z в тригонометрической форме имеет вид z=r*(cos(x)+i*sin(x)). На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим z=r*e^(ix). Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь r=|z|, x=arg(z).