19. Способ относительных разниц. Способ пропорционального деления (индексный способ).

Способ относительных разниц

Этот способ применяется только в мультипликативных моделях.

Для расчёта влияния первого фактора необходимо базовую величину результативного показателя умножить на относительный прирост первого фактора.Чтобы рассчитать влияние 2-ого фактора нужно к баз.величине результативного показателя прибавить изменение его за счёт первого фактора, а затем полученную сумму умножить на относительный прирост второго фактора. Влияние третьего фактора рассчитать аналогично второму.

В отличие от способов цепной подстановки и абсолютных разниц здесь значительно сокращается число вычислительных процедур. Поэтому этот способ рекомендуется применять, когда рассчитывается влияние большого комплекса факторов.

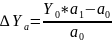
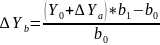
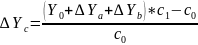
Способ пропорционального деления (индексный способ)

Применяется только в мультипликативных моделях. Для того, чтобы рассчитать влияние первого фактора нужно баз.величину результативного показателя умножить на разность между индексируемым фактором и единицей. Чтобы рассчитать влияние второго фактора нужно баз.величину результативного показателя умножить на индекс первого фактора и всё это умножить на разность между индексом второго фактора и единицы.

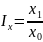
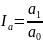
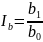
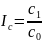
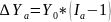
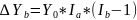
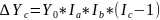
Исключение!!! Применение способа абсолютных разниц в мультипликативно-аддитивных моделях:

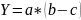
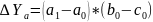
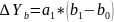
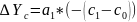
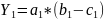
20. Интегральный метод. Способ логарифмирования.

Интегральный метод применяется для измерения влияния фак­торов в мультипликативных, кратных и кратно-аддитивных моделях. Его использование позволяет получать более точные результаты рас­чета влияния факторов по сравнению со способами цепной подста­новки, абсолютных и относительных разниц, поскольку дополни­тельный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится по­ровну между ними.

При его использовании исходят из того, что факторы изменяются независимо друг от друга, однако фактически они изменяются взаимосвязанно, в результате образуется некоторый неразложимый остаток, который прибавляется к величине влияния одного из факторов (как правило, последнего). В связи с этим величина влияния факторов на изменение результативного показателя колеблется в зависимости от места фактора в детерминированной модели. Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для определения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида.

Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. Как и при интегрировании, здесь результат расчёта также не зависит от месторасположения факторов в модели. По сравнению с интегральным методом логарифмирование обеспечивает более высокую точность расчётов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доле изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток – в ограниченности сферы применения.

В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения).

В связи со сложностью вычисления некоторых определенных интегралов и дополнительные сложностей, связанных с возможным действием факторов в противоположных направлениях, на практике используются специально сформированные рабочие формулы, приводимые в специальной литературе:

Способ логарифмирования применяется в мультипликативных и кратных моделях.

Схема определения следующая:

1. Строится факторная модель:

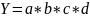
2. Определяется базисное (плановое) значение обобщённогопоказателя:

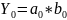
3. Определяется фактическое значение обобщённого показателя:

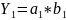
4. Определяется общее абсолютное отклонение обобщённого показателя:

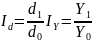
Вт.ч. за счёт фактора a:

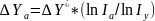
за счёт фактора b:

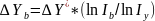
за счёт фактора c:

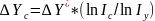
за счёт фактора d: