Завдання № 5 Розрахунок статично визначених балок на міцність і жорсткість при згинанні

5.1 Зміст завдання

5.1.1 Для заданої статично визначної балки визначити опорні реакції і побудувати епюри поперечних сил і згинальних моментів .

5.1.2 Визначити небезпечний переріз балки і з умови міцності при згині підібрати розміри заданого профілю балки.

Матеріал балки сталь Ст.3 для якої

5.1.3 Побудувати для заданого профілю епюри розподілу нормальних і дотичних напружень по небезпечному перерізу балки.

5.1.4 Використовуючи диференціальне рівняння пружної лінії балки визначити прогин посередині прольоту для двох опорної балки, для жорсткого затисненої балки – прогин кінця консолі.

5.2 Методичні вказівки до виконання завдання № 5

5.2.1 Складається розрахункова схема балки з зображенням діючих на неї навантажень. Відкидаються опори, а їх вплив на балку замінюється відповідними реакціями; вказуються позначення реакцій і попередньо прийняті їх направлення.

Реакції на опорах знаходять з рівнянь рівноваги балки, згідно з якими суми моментів усіх зовнішніх сил відносно опорних шарнірів дорівнюють нулю.

При обчисленні цих реакцій моменти вважають додатними, якщо вони діють за годинниковою стрілкою.

Для консольної балки з жорстко заробленим кінцем визначати реакції і реактивний момент в закладенні немає необхідності, оскільки вони виходять автоматично при побудові епюр

Якщо в результаті обчислень реакція виходить від'ємною, то на схемі потрібно змінити її напрямок на протилежний, і надалі вважати цю реакцію додатною.

Для контролю правильності знайдених реакцій використовується умова рівності нулю суми проекцій всіх сил на вертикальну вісь

5.2.2 Балка розбивається на ділянки, межами яких є точки прикладання зовнішніх зосереджених сил і моментів, а також точки початку дії і закінчення дії розподілених навантажень.

На розрахунковій схемі вказується початок і напрямок відліку відстані для кожної ділянки.

Нагадаємо, що при прямому згинанні в поперечних перерізах балки виникають два внутрішніх силових фактори - поперечна сила і згинальний момент , які визначаються методом перерізів.

Згідно з методом перерізів поперечна сила в даному перерізі чисельно дорівнює алгебраїчній сумі проекцій на вертикальну вісь всіх зовнішніх і реактивних сил, що діють по одну сторону від розглянутого перерізу.

Згинальний момент, що діє в поперечному перерізі чисельно дорівнює сумі моментів усіх зовнішніх і реактивних сил розташованих по одну сторону від перерізу, відносно центра тяжіння перерізу.

Скласти вирази поперечних сил і згинальних моментів в довільному перерізі на кожній ділянці балки.

При складанні даних виразів необхідно пам'ятати про правила знаків для внутрішніх силових факторів при згинанні.

При напрямі руху зліва на право, всі зовнішні і реактивні сили, що лежать ліворуч від перерізу, вважаються додатними, якщо вони спрямовані вгору, і від'ємними - якщо вони спрямовані вниз.

При напрямі руху справа на ліво, всі зовнішні і реактивні сили, що лежать правіше від перерізу вважаються додатними, якщо вони спрямовані вниз і від'ємними якщо спрямовані вгору.

При напрямі руху зліва на право, моменти зовнішніх і реактивних сил, що лежать зліва від перерізу, вважаються додатними, якщо вони намагаються повернути відсічену частину балки відносно даного перерізу за годинниковою стрілкою і вважаються від'ємними, якщо вони намагаються повернути відсічену частину балки відносно даного перерізу проти годинникової стрілки.

При напрямі руху з права на ліво, моменти зовнішніх і реактивних сил, що лежать справа від перетину вважаються додатними, якщо вони намагаються повернути відсічену частину балки відносно даного перерізу проти годинникової стрілки, і вважаються від'ємними, якщо вони намагаються повернути відсічену частину балки відносно даного перерізу по годинниковою стрілкою.

За отриманими значеннями поперечних сил і згинальних моментів будуються епюри .

При побудові епюр поперечних сил і згинальних моментів слід запам'ятати деякі правила, що випливають з диференціальних залежностей

а саме:

1. Якщо на ділянці балки відсутній розподілене навантаження, то епюра пряма лінія, паралельна поздовжньої осі балки. Епюра моментів на цій ділянці похила пряма.

2. Якщо на ділянці є розподілене навантаження, то епюра являє собою похилу пряму, а епюра квадратну параболу, звернену опуклістю назустріч навантаженні.

3. У перерізі, де поперечна сила дорівнює нулю згинальний момент досягає екстремального (максимального чи мінімального) значення.

4. У перерізі, де прикладена зовнішня зосереджена сила, перпендикулярна поздовжнього осі балки, епюра має стрибок на величину цієї сили, а епюра - має злам.

5. У перерізі, де прикладений зовнішній зосереджений момент, епюра , має стрибок на величину цього моменту. На епюрі це не відображається.

6. При побудові епюр, позитивні значення відкладаються вгору від осі епюри, а негативні значення - вниз.

5.2.3 Для балки, поперечні розміри якої по всій довжині постійні, небезпечним є той поперечний переріз, в якому виникає найбільший згинальний момент, який визначається з епюри .

Підбір поперечних розмірів балки з умови міцності при згині виконується за формулою

де – максимальний згинальний момент у небезпечному перерізі.

– допустиме нормальне напруження при згині.

– осьовий момент опору при згині.

Осьові моменти опору найпростіших симетричних перерізів обчислюються за такими формулами:

для прямокутника

для кола

Номер двотаврового перерізу, що має момент опору близький до необхідного, визначаємо за таблицею сорту моменту ( ).

При цьому необхідно виконати умову

5.2.4 При прямому поперечному згині прямого бруса в його поперечних перерізах виникають нормальні і дотичні напруження.

Нормальні напруження, що змінюються по висоті перерізу за лінійним законом, досягають найбільших значень в точках найбільш віддалених від нейтральної осі, в перерізах, де згинальний момент максимальний.

Максимальні нормальні напруження обчислюються за формулою

Для балок з пластичного матеріалу, що мають найпростіші симетричні перерізи, епюри нормальних напружень мають вигляд, показаний на малюнку

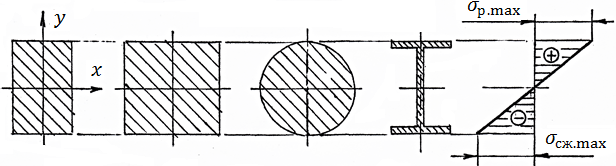
При побудові епюри σ максимальні нормальні напруження розтягу відкладають на розтягнутих волокнах балки, а максимальні нормальні стискаючі напруги , відкладають на стиснутих волокнах.

У найпростіших перетинах типу прямокутник, круг, двутавр, дотичні напруги змінюються по висоті перерізу за законом квадратної параболи, досягаючи найбільшого значення в точках нейтральної осі. У крайніх точках перерізів дотичні напруження дорівнюють нулю.

У загальному випадку дотичні напруження в будь-якій точці поперечного перерізу обчислюється за формулою Журавського

де – поперечна сила в перерізі

– статично момент відносно нейтральної осі тієї частини перерізу, яка розташована вище прямої проведеної через дану точку паралельно нейтральної осі.

– ширина перерізу на рівні розглянутої точки.

– осьовий момент інерції всього перерізу відносно нейтральної осі.

Для прямокутного перерізу найбільші дотичні напруження виникають в точках нейтральної осі і обчислюються за формулою

де – поперечна сила в перерізі

– площа поперечного перерізу балки.

Для круглого перерізу максимальні дотичні напруження також виникають в точках нейтральної осі і визначаються за формулою

Епюра дотичних напружень для балок прямокутного і круглого перерізів має вигляд

Для двотаврового перерізу максимальні дотичні напруження виникають в точках нейтральної осі

де – поперечна сила в перетині

– статичний момент площі пів розріз відносно нейтральної осі .

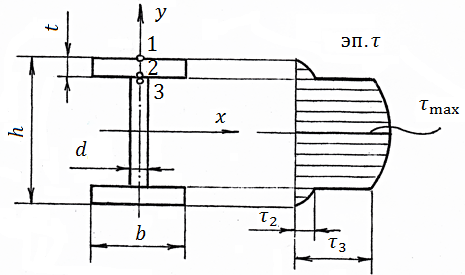
У верхній точці 1 двутавра дотичні напруги дорівнюють нулю.

У точці 3 розташованої безпосередньо над лінією проходить через нижню межу верхньої полиці двутавра дотичні напруження визначаються за формулою

У стінці двутавра в точці 3 розташованої безпосередньо під точкою 2 дотичні напруження дорівнюють

5.2.5 Деформації балок при прямому згині:

– кути повороту , і прогини поперечних перерізів, визначаються шляхом інтегрування наближеного диференціального рівняння пружної лінії

де – рівняння згинаючих моментів

жорсткість перерізу

Інтегруючи це рівняння, отримуємо рівняння кутів нахилу дотичних до пружної лінії, рівні кутах повороту відповідних поперечних перерізів

Повторне інтегрування дає рівняння прогинів або рівняння пружної лінії

В отриманих рівняннях постійні інтегрування, що позначаються є відповідно кут повороту і прогин перетину на початку координат, помножені на жорсткість перерізу

Початок координат приймається в центрі тяжіння крайнього лівого поперечного перерізу балки.

Значення постійних визначають з граничних умов, що залежать від способу закріплення балки, при цьому може мати місце один з трьох варіантів значень :

1. лівий кінець балки защемлений

2. лівий кінець балки шарнірно обпертий

3. лівий кінець балки вільний

При інтегруванні диференціального рівняння пружної лінії застосовують такі три прийоми:

1. Додаток від зосередженого моменту у виразі для записують у вигляді , де - абсциса перерізу в якому прикладений момент .

2. Інтегрування ведуть без розкриття дужок.

3. Якщо на балці є розподілене навантаження, яке не доходить до перерізу, де визначається прогин, то її продовжують до цього перерізу і прикладають протилежно спрямоване компенсуюче навантаження тієї ж інтенсивності.

Як правило, необхідно скласти рівняння згинаючих моментів для останньої ділянки балки. Тому що з нього легко отримати рівняння для будь-якої попередньої ділянки, виключаючи складові, відповідні навантаженням, прикладених до балки правіше розглянутої ділянки.

Данні для виконання завдання № 5 взяти з таблиці № 8 згідно свого порядкового номеру.

Таблиця № 8
№	№ рисунка	a	p		q	M