Завдання № 3 Визначення геометричних характеристик плоских перерізів

3.1 Зміст завдання

Для заданого складного перерізу визначити головні центральні моменти інерції.

3.2 Методичні вказівки до виконання завдання.

3.2. Згідно розмірами в масштабі накреслити заданий переріз, зробити його розбиття на прості фігури для яких легко обчислити площі та осьові моменти інерції.

Вибрати допоміжні осі, причому провести їх таким чином, щоб вони перетнули якомога більше число центрів тяжіння простих фігур.

3.2.2 Визначити координати центрів тяжіння фігур щодо допоміжних осей та нанести ці координати на креслення перерізу.

Визначення положення центру тяжіння площі проводиться за допомогою статичних моментів. Статичні моменти можуть бути як додатними, так і від'ємними, а якщо статичний момент визначається відносно осі, що проходить через центр тяжіння, то він дорівнює нулю.

Координати центру тяжіння всього складного перерізу обчислюються за формулами:

де – площа, статичні моменти, і координати центру тяжіння всього заданого перерізу відносно допоміжних осей .

– площі і координати центрів тяжіння окремих простих фігур відносно тих самих осей .

3.2.3 Визначають власні осьові моменти інерції окремих простих фігур за формулами наведених у таблиці № 5.

3.2.4 Осьові моменти інерції окремих фігур відносно допоміжних осей обчислюються за формулами переходу до паралельних осей

де – порядковий номер фігури

– власні осьові моменти інерції простих фігур.

– площі простих фігур.

3.2.5 Осьові моменти інерції відносно допоміжних осей для всього перерізу визначаються шляхом складання відповідних осьових моментів інерції окремих фігур.

Таблиця № 5
№	Форма фігури	Площі	Осьові моменти інерції
1.
2.
3.
4.

3.2.6 Осьові моменти інерції відносно центральних осей складного перерізу визначаються за формулами переходу до паралельних осей. При цьому потрібно пам’ятати, що при переході від довільних осей до центральних, величини переносних моментів віднімаються:

3.2.7 Номер схеми варіанту завдання № 3 вибрати відповідно свого порядкового номеру у списку групи.

3.4 Приклад виконання завдання № 3

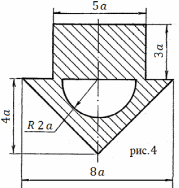
Визначити головні центральні моменти інерції складного перерізу представленого на малюнку

Розв’язання:

3.4.1 Накреслимо заданий переріз і проставляємо всі необхідні розміри.

Розбиваємо переріз на наступні прості фігури:

1 – квадрат з розмірами

2 – трикутник з розмірами и

3 – півколо

Позначаємо центри тяжіння простих фігур і будуємо для кожної, центральні вісі.

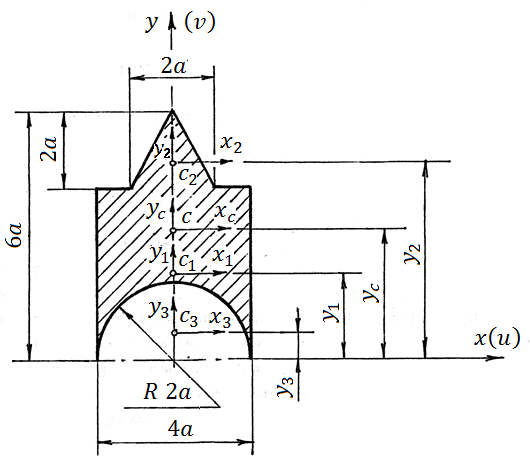
3.4.2 Вибираємо допоміжні осі таким чином, щоб вісь перетинала в даному випадку центри тяжіння всіх простих фігур, проходячи через точки а вісь пройде вздовж основи заданої фігури тобто співпадає з діаметром півкола вирізу.

Далі, визначаємо координати центрів тяжіння окремих фігур, відносно допоміжних осей , а також площі окремих фігур і всього перерізу в цілому.

Для квадрата

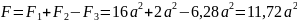
3.4.3 Обчислюємо статичні моменти і визначаємо положення центру тяжіння заданого перерізу

3.4.4 За допомогою формул наведених у таблиці № 5 визначаємо власні центральні моменти інерції окремих простих фігур.

Для квадрата
Для трикутника
Для півкола

Центробіжні моменти інерції всіх простих фігур входять в заданий переріз дорівнюють нулю, тому що їх центральні осі для кожної з них одночасно є і головними осями.

3.4.5 Обчислюємо моменти інерції окремих фігур відносно допоміжних осей .

Оскільки вісі співпадають з , то

Визначаємо моменти інерції всього перерізу відносно допоміжних осей

3.4.6 Обчислимо значення головних центральних моментів інерції всього перерізу згідно формулам