МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

Чорноморський державний університет імені Петра Могили

Факультет еколого-медичних наук

Кафедра медичних приладів та систем

Методичний посібник

до виконання розрахунково-графічних завдань

з прикладної механіки

Розділ І

«Опір матеріалів»

Зміст

Вступ …………………………………………………………………………………3

1. Завдання № 1 «Розрахунок брусів на розтяг й стиснення» ……….……………4

2. Завдання №2 «Розрахунок статично невизначених стрижньових систем на міцність при розтягуванні й стисненні» ………………………………………….27

3. Завдання №3 «Визначення геометричних характеристик плоских перерізів»……………………………………………………………………………46

4. Завдання №4 «Розрахунок статично невизначеного валу на міцність при крученні»……………………………………………………………………………57

5. Завдання №5 «Розрахунок статично визначених балок на міцність та жорсткість при згинанні» ………………………………………………………………………72

6. Рекомендована література ………………………………………………………..91

Вступ

В даній збірці наведені варіанти розрахунково-графічних завдань з курсу «Опір матеріалів», а також методичні вказівки до виконання цих завдань.

Завдання оформлюються у відповідності до вимог ЄСКД на листах формату А4.

При розв'язуванні кожної задачі спочатку необхідно записати її умову. Всі числові величини мають бути записані в системі СІ. Епюри й розрахункові схеми виконуються олівцем з вказівкою необхідних розмірів. Розрахунки мають супроводжуватись короткими поясненнями.

Всі розрахунки необхідно представити наступним чином: спочатку записується шукана величина, потім - формула, далі підстановка числових значень всіх величин, що входять до розрахункової формули в тому порядку, як вони записані в формулі, а потім, минувши проміжні обчислення, записується відповідь з вказівкою розмірності.

При проведенні розрахунків в числових значеннях необхідно утримувати чотири значущі цифри.

Перед тим, як приступити до виконання того або іншого завдання, студенту необхідно вивчити теорію питання, що розглядається.

Студент має вміти використовувати метод перерізів для визначення внутрішніх силових факторів в елементах конструкцій при різних видах деформацій, скласти й вирішити розрахункову схему, знаходити положення небезпечних перерізів й визначати найбільші напруження в небезпечних точках небезпечних перерізів, складати умови міцності й жорсткості для найбільш навантажених елементів конструкцій.

Відмічені викладачем помилки виправляються на зворотній стороні листа пояснювальної записки.

Ні в якому випадку не допускається при виправленні що-небудь витирати й тим більше вилучати листи, рисунки з перевіреної викладачем пояснювальної записки. Вставка додаткових листів до завдання при виправленні не допускається.

Правильно виконане завдання (з урахуванням виправлень) має бути захищено.

Завдання № 1 Розрахунок брусів на розтяг її стиснення

1.1 Зміст завдання

Дане завдання складається з двох задач:

Задача 1. Для заданого статично визначеного ступінчастого бруса провести розрахунок й побудувати епюри повздовжніх сил , нормальних напружень і переміщень поперечних перерізів від дії прикладених сил з врахуванням власної ваги.

Задача 2. Для бруса, жорстко закріпленого обома кінцями й навантаженого вздовж осі силами, прикладеними в його проміжних перерізах, побудувати епюри повздовжніх сил , нормальних напружень і переміщень . Виконати перевірку правильності вирішення задачі, використовуючи рівність потенційної енергії деформації бруса й роботи зовнішніх сил, прикладених до бруса.

1.2 Методичні вказівки до виконання задачі 1 завдання № 1

1.2.1 Накреслити по можливості в масштабі заданий брус.

1.2.2 Розбити брус на ділянки. Границями ділянок слугують місця зміни площі поперечного перерізу бруса і перерізи, в яких прикладена зовнішня сила.

1.2.3 Повздовжня сила в поперечному перерізі знаходиться методом перерізів. Довільним перерізом, що проходить через кожну ділянку, розрізаємо брус на дві частини, одну з яких відкидаємо.

Так як направлення повздовжньої сили в кожному перерізі невідомо, то при складанні рівняння рівноваги завжди будемо направляти її від перерізу.

Розглядаючи рівновагу частини бруса, що залишилася, з рівняння статики визначаємо повздовжню силу, яка чисельно рівна алгебраїчній сумі проекцій всіх зовнішніх сил, діючих по одну сторону від перерізу, на вісь бруса.

4. Нормальне напруження в січенні бруса підраховується за формулою

де – площина січення бруса.

1.2.5 Переміщення довільного січення бруса дорівнює деформації частини бруса розташованої між розглядаємим січенням та січенням прийнятим за початок відліку.

Найбільш узагальненому вигляді використовуючи закон Гука переміщення довільного січення першої ділянки можна записати в наступному вигляді.

де – модуль повздовжньої пружності матеріалу бруса.

При обчисленні переміщень наступних ділянок необхідно використовувати переміщення попередньої ділянки .

1.2.6 Данні для виконання задачі 1 взяти з таблиці №1 згідно свого порядкового номера.

Таблиця №1
№	Номер рисунку
1	1	1,0	2,0	1,2	2,6
2	2	1,2	2,0	2,4	1,4
3	3	1,4	2,2	0,5	1,6
4	4	1,6	2,4	1,4	2,0
5	5	1,8	2,6	2,0	1,5
6	6	2,0	1,2	0,6	1,3
7	7	2,2	1,4	1,5	0,8
8	8	2,4	1,6	0,5	-
9	9	2,6	1,8	1,8	-
10	10	3,0	2,0	1,6	0,5
11	11	1,0	2,2	0,4	-
12	12	1,4	2,4	2,2	-
13	13	1,6	2,8	1,5	2,2
14	14	1,8	3,2	0,8	0,4
15	15	2,8	2,0	1,7	0,7
16	16	2,5	1,5	1,4	2,8
17	17	1,2	2,4	0,7	0,5
18	18	1,0	1,2	2,0	0,8
19	19	1,5	1,0	1,6	-
20	20	1,8	1,4	0,6	-
21	21	1,4	2,0	0,4	0,8
22	22	2,0	3,0	1,8	-
23	23	1,2	1,8	2,2	-
24	24	2,4	3,0	0,8	0,4
25	1	1,2	1,6	1,4	2,0
26	5	1,4	2,0	1,8	1,4
27	10	2,4	3,2	1,4	0,8
28	15	2,0	1,6	1,6	0,6
29	20	1,4	2,02	0,8	-
30	30	5,4	2,0	-	-

1.3 Приклад виконання задачі 1 завдання № 1

Для ступінчастого бруса з жорстко защемленим верхнім кінцем й навантаженого вздовж осі силами необхідно побудувати епюри повздовжніх сил, нормальних напружень й переміщень з урахуванням власної ваги.

;

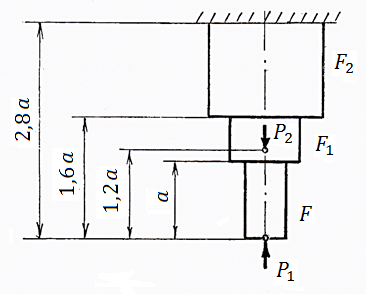
- питома вага матеріалу бруса,

- густина матеріалу бруса,

- прискорення вільного падіння,

- площа поперечного перерізу першої ступені бруса,

- площа поперечного перерізу другої ступені бруса,

- площа поперечного перерізу третьої ступені бруса.

Розв’язання:

Розіб'ємо брус на окремі ділянки, починаючи від вільного кінця. Нагадаємо, що границями ділянок є перерізи, в яких прикладені зовнішні сили, і місце зміни розмірів поперечного перерізу.

Таким чином, заданий брус має чотири ділянки.

1. Поздовжня сила в поперечному перерізі знаходиться за допомогою методу перерізів. Для цього довільним перерізом, що проходить через кожну ділянку, розрізаємо брус на дві частини й відкидаємо верхню частину.

Розглядаючи рівновагу нижньої частини бруса, що залишилася, з рівняння рівноваги статики знаходимо нормальну силу для кожної ділянки.

Проводимо переріз 1-1 на ділянці та розглядаємо рівновагу залишеної нижньої частини, попереднього проектуючи зовнішні і внутрішні сили на вісь .

; , де ;

, при

при .

Проводимо переріз 2-2 на ділянці

; , де ;

,

при

при .

Проводимо переріз 3-3 на ділянці

; ,

де ;

при ;

при .

Проводимо переріз 4-4 на ділянці

;

де ;

,

при ;

при .

Обчисливши значення повздовжньої сили на кожній ділянці ступінчастого бруса, будуємо епюру .

2. Нормальне напруження в перерізі кожної ділянки визначають, використовуючи значення повздовжньої сили.

Ділянка I

при ;

при .

Ділянка II

при

при

Ділянка III

де

при

при

Ділянка IV

при

при

Визначивши значення нормальних напружень в перерізах ділянок, будуємо епюру нормальних напружень .

3. Використовуючи закон Гука визначаються довільні переміщення січень бруса.

Так як брус має жорстке закладення в верхній частині, то за початок відліку приймаємо переріз в закладенні.

Ділянка IV

де

при

Ділянка III

де

Ділянка II

де

Ділянка I

де

Використовуючи отримані значення переміщень, будуємо епюру .

1.4 Методичні вказівки до виконання задачі 2 завдання № 1

1.4.1 Визначити ступінь статичної невизначеності системи(ступінчастого бруса).

Статично невизначеними називаються бруси, повздовжні зусилля в яких не можуть бути визначені за допомогою лише методу перерізів.

Ступінь статичної невизначеності бруса - це різниця між загальним числом невідомих сил й кількістю рівнянь рівноваги, які можна скласти для даного бруса.

1.4.2 При розрахунку статично невизначених брусів необхідно скласти додаткові рівняння, які враховують характер деформації системи. Ці рівняння називаються рівняннями переміщень.

Кількість рівнянь переміщень, необхідних для розрахунку статично невизначеного бруса, визначається ступінню його статичної невизначеності.

1.4.3 Після складення необхідного числа рівнянь переміщень визначаються внутрішні силові фактори (повздовжні сили, напруження й переміщення), що виникають в перерізах бруса, відповідно до методичних вказівок до виконання задачі №1 даного завдання.

1.4.4 Контроль правильності розв'язання задачі виконується на основі рівності потенційної енергії пружної деформації бруса і роботи прикладених до нього зовнішніх сил.

Потенційна енергія деформації бруса ступінчасто-змінного поперечного перерізу, навантаженого зосередженими силами, визначається за формулою:

де – повздовжня сила в поперечному перерізі бруса на -ділянці,

– відповідно площа поперечного перерізу бруса на -ділянці й довжина цієї ділянки,

– число ділянок, що розрізняються значенням напружень.

У випадку дії на брус розподілених по його довжині повздовжніх навантажень або при безперервній зміні розмірів поперечних перерізів бруса потенційна енергія деформації, що накопичується у всьому брусі, буде визначатися виразом

Робота зовнішніх зосереджених сил визначається за формулою

де – число зовнішніх сил ,

– переміщення поперечного перерізу, в якому прикладена сила , по напряму цієї сили.

1.4.5 Данні для виконання задачі 2 взяти з таблиці № 2 відповідно до свого порядкового номера.

Таблиця №2									і
№	Номер рисунку
1	1	1,0	3,0				1,2	0,8
2	2	1,2	2,8				-	-
3	3	1,4	2,6				1,0	2,0
4	4	1,6	2,4				-	-
5	5	1,8	2,2				0,9	2,5
6	6	2,0	4,0				1,8	0,7
7	7	1,1	3,8				2,2	1,1
8	8	1,3	3,6				1,3	0,9
9	9	1,5	3,4				-	-
10	10	1,7	3,2				1,6	1,0
11	11	1,9	3,0				-	-
12	12	2,2	6,0				0,5	3,0
13	13	2,4	5,8				2,0	1,2
14	14	2,6	5,6				-	-
15	15	2,8	5,4				1,0	2,4
16	16	3,0	5,2				4,2	1,4
17	17	5,0	1,0				0,7	3,2
18	18	4,8	1,2				-	-
19	19	4,6	1,4				1,6	1,0
20	20	4,4	1,6				1,4	2,8
21	21	4,2	1,8				-	-
22	22	4,0	2,0				3,0	1,5
23	23	1,2	4,0				-	-
24	24	1,4	3,8				1,1	5
25	25	1,6	3,6				1,5	1,2
26	26	1,8	3,4				-	-
27	27	2,0	3,2				2,2	1,0
28	28	5,0	3,0				0,9	2,6
29	29	5,2	2,8				1,2	0,6
30	20	5,4	2,0				-	-

1.5 Приклад виконання задачі 2 завдання № 1

Для бруса з жорстко защемленими обома кінцями й навантаженого в проміжних перерізах зовнішніми силами напрямленими вздовж його осі, побудувати епюри повздовжніх сил, нормальних напружень й переміщень.

Виконати перевірку правильності розв'язання задачі, використовуючи рівність потенційної енергії деформації бруса і роботи зовнішніх сил, прикладених до бруса.

Розв'язок:

1.5.1 В закладеннях бруса виникають реакції, направлені вздовж його осі. Для лінійної системи сил статика дає одне рівняння рівноваги:

або

Оскільки невідомих реактивних сил дві, а рівняння рівноваги одне, то задана система один раз статично невизначена.

1.5.2 Для складання рівняння переміщень відкинемо верхнє закладення , а її дію на брус замінимо реактивною силою .

Даний брус має чотири ділянки навантаження.

Повздовжня сила, діюча в перерізах І ділянки, визначається з рівняння:

Повздовжня сила, діюча в перерізах ІІ ділянки, визначається з рівняння:

звідки

Повздовжня сила, діюча в перерізах ІІІ ділянки, визначається з рівняння:

звідки

Повздовжня сила, діюча в перерізах VI ділянки, визначається з рівняння:

звідки

Визначимо повздовжні деформації ділянок:

І ділянка довжина :

ІІ ділянка довжиною :

ІІІ ділянка довжиною :

IV ділянка довжиною :

Оскільки отриманий брус еквівалентний заданому, то додаткове рівняння переміщень отримуємо з тієї умови, що сума повздовжніх переміщень всіх ділянок бруса рівна нулю, так як відстань між закладеннями А і В змінитися не може.

Після визначення реакції в верхньому закладенні даний брус представляє собою статично визначену систему, навантажену відомими силами.

Побудова епюри повздовжніх сил, нормальних напружень й переміщень для статично визначеного бруса виконується аналогічно прикладу розглянутому в задачі №1.

1.5.3 Визначення повздовжніх сил.

Поводимо переріз 1-1 на ділянці І. Складемо рівняння рівноваги всіх сил що діють на відсічену частину бруса в проекції на вісь :

Для переріз 2-2 ділянці ІІ рівняння рівноваги має вид:

Для перерізу 4-4 ділянці IV рівняння рівноваги має вид:

За обчисленими значеннями повздовжніх сил на ділянках бруса будуємо епюру .

1.5.4 Визначення нормальних напружень.

Нормальне напруження на І ділянці бруса:

Нормальне напруження на ІІ ділянці:

Нормальне напруження на ІІІ ділянці:

Нормальне напруження на IV ділянці:

1.5.5 Визначення повздовжніх переміщень.

За початок відліку переміщень приймаємо переріз бруса в верхньому закладенні, при цьому переміщення вниз вважаємо додатними.

Ділянка І

Ділянка ІІ

Ділянка ІІІ

Ділянка IV

1.5.6 перевірка правильності розв’язання задачі.

Потенційна енергія пружної деформації заданого бруса є рівною:

де – потенційні енергії деформації ділянок ступінчастого бруса.

Підставляючи в даний вираз відповідні значення повздовжніх сил, площ поперечних перерізів й довжин ділянок бруса, отримаємо:

Робота зовнішніх переміщень зосереджених сил діючих вздовж осі бруса, є рівною:

– переміщення точки прикладення сили , викликане дією всіх прикладених до бруса сил.

– переміщення точки прикладення сили , викликане дією всіх прикладених до бруса сил.

Значення беремо з побудованої епюри переміщень.

Таким чином, рівність виконується.