Теория массового обслуживания

1. Предмет и задачи В производственной деятельности и повседневной жизни часто возникают ситуации, когда появляется необходимость в обслуживании требований или заявок поступающих в систему. Часто встречаются ситуации, в которых необходимо пребывать в ситуации ожидания. Примерами тому может служить очередь покупателей у касс большого магазина, группа пассажирских самолетов, ожидающих разрешения на взлет в аэропорте, ряд вышедших из строя станков и механизмов, поставленных в очередь для починки в ремонтном цехе предприятия и т.д. Иногда системы обслуживания обладают ограниченными возможностями для удовлетворения спроса, и это приводит к образованию очередей. Как правило, ни время возникновения потребностей в обслуживании, ни продолжительность обслуживания заранее не известны. Избежать ситуации ожидания чаще всего не удается, но можно сократить время ожидания до какого-то терпимого предела.

Предметом теории массового обслуживания являются системы массового обслуживания (СМО). Задачами теории массового обслуживания являются анализ и исследование явлений, возникающих в системах обслуживания. Одна из основных задач теории заключается в определении таких характеристик системы, которые обеспечивают заданное качество функционирования, например, минимум времени ожидания, минимум средней длины очереди. Цель изучения режима функционирования обслуживающей системы в условиях, когда фактор случайности является существенным, контролировать некоторые количественные показатели функционирования системы массового обслуживания. Такими показателями, в частности являются среднее время пребывания клиента в очереди или доля времени, в течение которой обслуживающая система простаивает. При этом в первом случае мы оцениваем систему с позиции «клиента», тогда как во втором случае мы оцениваем степень загруженности обслуживающей системы. Путем варьирования операционными характеристиками обслуживающей системы может быть достигнут разумный компромисс между требованиями «клиентов» и мощностью обслуживающей системы.

В качестве показателей СМО могут применяться также такие величины как среднее число заявок в очереди, вероятность того, что число заявок в очереди превысит какое-то значение и т.д.

Система - совокупность элементов, связей между ними и цели функционирования. Любой системе массового обслуживания характерна структура, которая определяется составом элементов и функциональными связями.

Основные элементы системы следующие:

1. Входящий поток требований (интенсивность входящего потока );

2. Каналы обслуживания (число каналов n, среднее число занятых k, производительность );

3. Очередь требований (среднее число заявок z, среднее время пребывания одной заявки t );

4. Выходящий поток требований (интенсивность входящего потока ).

2. Классификация систем массового обслуживания По количеству каналов СМО подразделяют на одноканальные и многоканальные. По месту нахождения источников заявок системы массового обслуживания можно разделить на:

 закрытые – источник в системе и оказывает на нее влияние;

 открытые – вне системы и не оказывает влияния.

По фазам обслуживания СМО можно разделить на:

 однофазные – один этап обслуживания,

 многофазные – два и более этапов.

Системы массового обслуживания (СМО) по условиям ожидания делятся на два основных класса: СМО с отказами и СМО с ожиданием. В СМО с отказами заявка, поступающая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует (пример - звонок по телефону). В СМО с ожиданием заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь на обслуживание.

СМО с ожиданием подразделяются на разные виды в зависимости от того, как организована очередь: с ограниченной или неограниченной длиной ожидания, с ограниченным временем ожидания и т.д.

Для классификации СМО важное значение имеет дисциплина обслуживания, определяющая порядок выбора заявок из числа поступивших и порядок распределения их между свободными каналами. Дисциплина обслуживания – правила, по которым действуют СМО. По этому признаку обслуживание требования может быть организованно:

1. по принципу «первый пришел – первый обслужен»;

2. по принципу «первый пришел – последним обслужен» (например, отгрузка однородной продукции со склада).

3. случайно;

4. с приоритетом. При этом приоритет может быть абсолютным (более важная заявка вытесняет обычную) и относительным (важная заявка получает лишь «лучшее» место в очереди).

При анализе случайных процессов с дискретным состояниями удобно пользоваться геометрической схемой – так называемым графом состояний.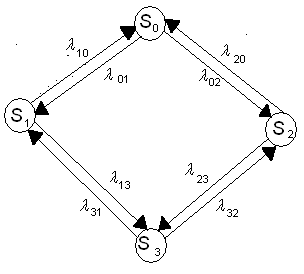

Пример. Устройство S состоит из двух узлов,

каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное случайное время. Возможные состояния системы: S₀ – оба узла исправны; S₁ – первый узел ремонтируется, второй исправен; S₂ – первый узел исправен, второй ремонтируется; S₃ – оба узла ремонтируются.

3. Входящий поток требований Общей особенностью всех задач, связанных с массовым обслуживанием, является случайный характер исследуемых явлений. Количество требований на обслуживание, временные интервалы между их поступлениями и длительность обслуживания случайны. Поэтому основным аппаратом описания систем обслуживания оказывается аппарат теории случайных процессов, в частности, марковских. Для исследования процессов, происходящих в этих системах, применяются методы имитационного моделирования.

Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Это означает, что состояние СМО меняется скачком в случайные моменты появления каких-либо событий (появление новой заявки, приоритета обслуживания, окончания обслуживания).

Под случайным (стохастическим, вероятностным) процессом понимается процесс изменения во времени состояния какой-либо системы в соответствии с вероятностным законом. Заявки на обслуживание в СМО обычно поступают не регулярно (например, поток вызовов на телефонной станции, поток отказов компьютеров, поток покупателей и т.д.), образуя так называемый поток заявок (или требований).

Поток характеризуется интенсивностью λ – частотой появления событий или средним числом событий, поступающих в СМО в единицу времени.

Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени (поток изделий на конвейере сборочного цеха).

Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности у стационарного потока λ(i)= λ (поток автомобилей на проспекте в часы пик).

Поток событий называется потоком без последствий, если для любых два непересекающихся участков времени – τ₁ и τ₂ – число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие (поток людей, входящих в метро или поток покупателей, отходящих от кассы).

Поток событий ординарен, если события появляются в нем поодиночке, а не группами (поток поездов – ординарен, поток вагонов – нет).

Поток событий называется простейшим, если он одновременно стационарен, ординарен и не имеет последствий.

Ординарный поток заявок без последствий описывается распределением (законом) Пуассона.

Простейший поток в теории массового обслуживания играет такую же роль, как и нормальный закон в теории вероятностей. Главная его особенность заключается в том, что при сложении нескольких независимых простейших потоков образуется суммарный поток, который также близок к простейшему.

Каждому событию соответствует момент t, в который это событие произошло. Т – интервал между двумя моментами времени. Поток событий – независимая последовательность моментов t.

Для простейшего потока с интенсивностью λ вероятность попадания на элементарный (малый) отрезок времени Δt хотя бы одного события потока равна .

Ординарный поток заявок без последствий описывается распределением (законом) Пуассона с параметром λτ:

, (1)

для которого математическое ожидание случайной величины равно ее дисперсии: .

В частности, вероятность того, что за время τ не произойдет ни одного события (m=0), равна

. (2)

Пример. На автоматическую телефонную линию поступает простейший поток вызовов с интенсивностью λ=1,2 вызовов в минуту. Найти вероятность того, что за две минуты: а) не придет ни одного вызова; б) придет ровно один вызов; в) придет хотя бы один вызов.

Решение. а) Случайная величина Х – число вызовов за две минуты – распределена по закону Пуассона с параметром λτ =1,2·2=2,4. Вероятность того, что вызовов не будет (m=0), по формуле (2):

.

б) Вероятность одного вызова (m=1):

.

в) Вероятность хотя бы одного вызова:

.

4. Предельные вероятности состояний Если число состояний системы конечно и из каждого из них можно за конечное число шагов перейти в любое другое состояние, то предельные вероятности существуют.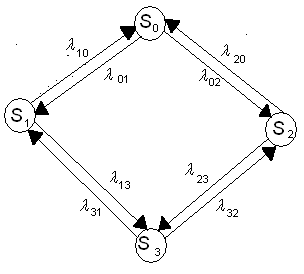

Рассмотрим математическое описание Марковского процесса с дискретными состояниями и непрерывным временем на примере процесса, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния S_i в S_j происходят под воздействием простейших потоков событий с интенсивностями состояний λ_ij (i,j=0,.1,2,3).

Так как переход системы из состояния S₀ в S₁ будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния S₁ в S₀ – под воздействием потока и событий, связанных с окончанием ремонтов первого узла и т.д.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным. Рассматриваемая система имеет четыре возможных состояния: S₀, S₁, S₂, S₃. Назовем вероятностью i-го состояния вероятность p_i(t) того, что в момент t система будет находиться в состоянии S_i. Очевидно, что для любого момента t сумма вероятностей всех состояний равна единице: .

Предельная вероятность состояния S_i имеет – показывает среднее относительное время пребывания системы в этом состоянии (если предельная вероятность состояния S₀, т.е. p₀ =0,5, то это означает, что в среднем половину времени система находится в состоянии S₀).

Для системы S с графом состояний, изображенном на рис. система линейных алгебраических уравнений, описывающих стационарный режим, имеет вид (также называется системой уравнений Колмогорова):

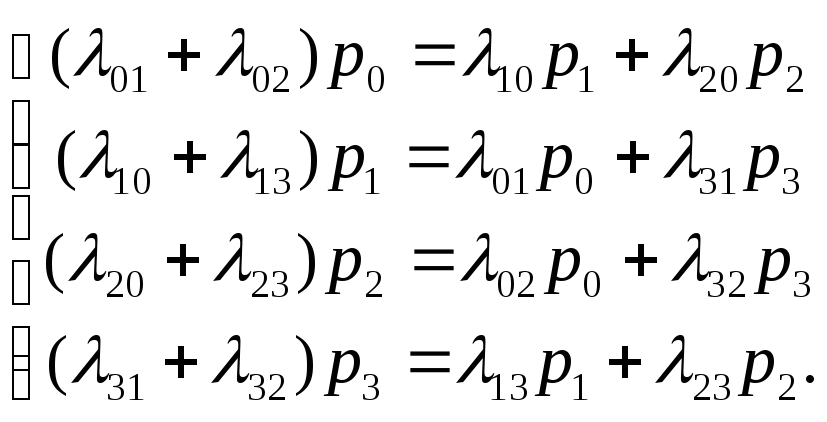(3)

Данная система может быть получена по размеченному графу состояний, руководствуясь правилом, согласно которому в левой части уравнений стоит предельная вероятность данного состояния p_i, умноженная на суммарную интенсивность всех потоков, выходящих из i-го состояния, равная сумме произведений интенсивности всех потоков, входящих из i-е состояние на вероятности тех состояний, из которых эти потоки исходят.

Пример. Найти предельные вероятности для системы, граф состояний которого изображен на рис. выше. при λ01=1, λ02=2, λ10=2, λ13=2, λ20=3, λ23=1, λ31=3, λ32=2.

Система алгебраических уравнений для этого случая согласно (3) имеет вид:

 

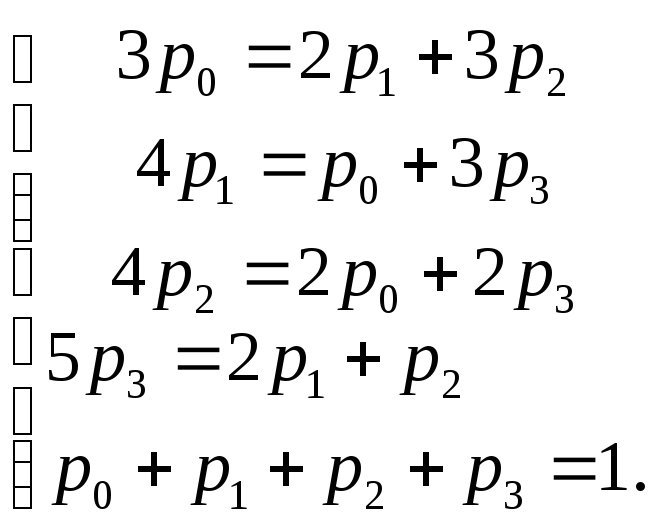
Решив линейную систему уравнений, получим p0 = 0,4, p1 = 0,2, p2 = 0,27, p3 = 0,13; т.е. в предельном стационарном режиме система S в среднем 40% времени будет находиться в состоянии S0 (оба узла исправны), 13% в состоянии S1 (первый узел ремонтируется, второй работает), 27% - в состоянии S2 (второй узел ремонтируется, первый работает) и 13% в состоянии S3 (оба узла ремонтируются).

Определим чистый доход от эксплуатации в стационарном режиме рассмотренной системы S в условиях, что в единицу времени исправная работа узла один и узла два приносит доход соответственно 10 и 6 денежных единиц, а их ремонт требует соответственно затрат 4 и 2 денежных единицы. Оценим экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Для решения этой задачи с учетом полученных значений p0, p1, p2, p3 определим долю времени исправной работы первого узла, т.е. p0+p2= 0,4+0,27 = 0,67 и долю времени исправной работы второго узла p0+p1= 0,4+0,2 = 0,6. В то же время первый узел находится в ремонте в среднем долю времени равную p1+p3= 0,2+0,13 = 0,33, а второй узел p2+p3= 0,27+0,13 = 0,40. Поэтому средний чистый доход в единицу времени от эксплуатации системы равен Д=0,67·10+0,6·6–0,33·4–0,4·2=8,18 ден.ед. уменьшение вдвое среднего времени ремонта каждого узла будет означать увеличение вдвое интенсивностей потока «окончания ремонтов» каждого узла, т.е. теперь λ10=4, λ20=6, λ31=6, λ32=4 и система уравнений, описывающая стационарный режим системы S, будет иметь вид:

 .

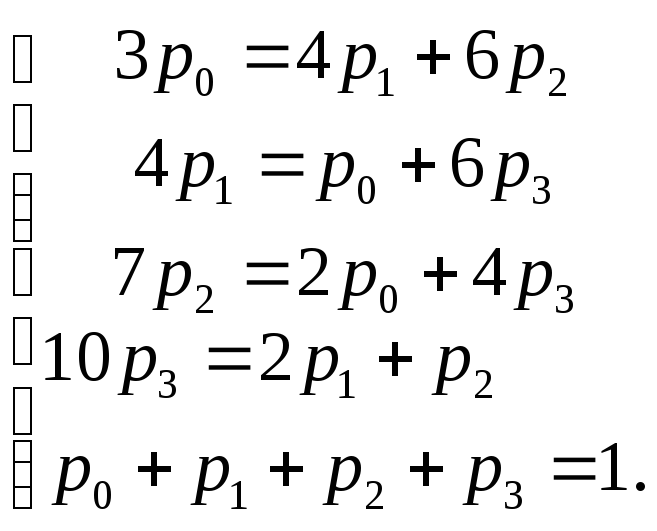Решив систему получим p0 = 0,6, p1 = 0,15, p2 = 0,2, p3 = 0,05. Учитывая, что p0+p2= 0,6+0,2 = 0,8,

p0+p1= 0,6+0,15 = 0,75, p1+p3= 0,15+0,05 = 0,2, p2+p3= 0,2+0,05 = 0,25, а затраты на ремонт первого и второго узла составляют соответственно 8 и 4 ден.ед., вычислим чистый средний доход в единицу времени: Д1=0,8·10+0,75·6–0,2·8–0,25·4=9,99 ден.ед.

Так как Д1 больше Д (примерно на 20%), то экономическая целесообразность ускорения ремонта узлов очевидна.

5. Процесс размножения и гибели Рассматриваемый в СМО процесс размножения и гибели характеризуется тем, что если все состояния системы пронумеровать S₁, S₂, …, S_n то из состояния S_k (k<n) можно попасть либо в состояние S_k-1, либо в состояние S_k+1.

Для предельных вероятностей характерна следующая система уравнений:

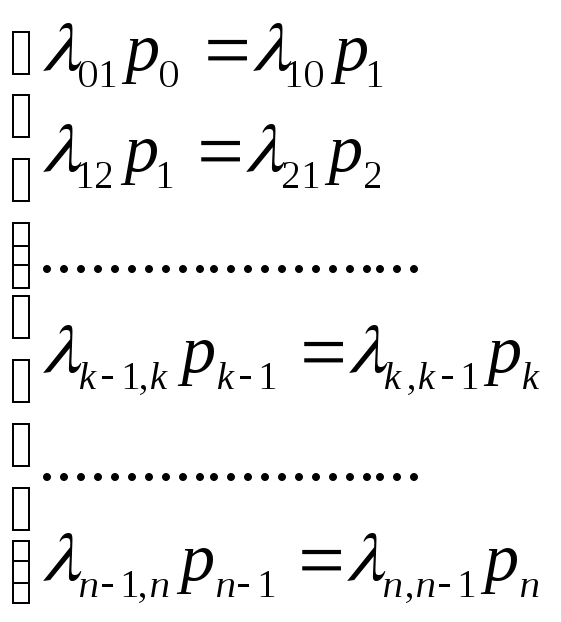(4)

к которой добавляется условие:

. (5)

Из этой системы можно найти предельные вероятности. Получим:

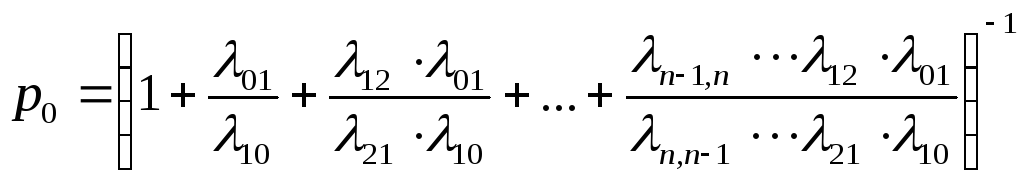, (6)

, , …, . (7)

Пример. Процесс гибели и размножения представлен графом. (рис).

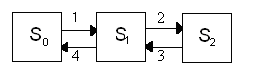
Найти предельные вероятности состояний.

Решение. По формуле (6) найдем ,

по (7) , ,

т.е. в установившемся стационарном режиме в среднем 70,6% времени система будет находиться в состоянии S₀, 17,6% – в состоянии S₁ и 11,8% – в состоянии S₂.

6. Системы с отказами В качестве показателей эффективности СМО с отказами будем рассматривать:

А – абсолютную пропускную способность СМО, т.е. среднее число заявок, обслуживаемых в единицу времени,

Q – относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;

– вероятность отказа, т.е. того, что заявка покинет СМО необслуженной;

– среднее число занятых каналов (для многоканальной системы).