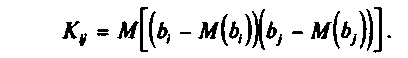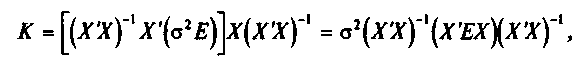Ковариационная матрица и ее выборочная оценка
Вариации
оценок параметров будут в конечном
счете определять точность уравнения
множественной регрессии. Для их измерения
в многомерном регрессионном анализе
рассматривают так называемую ковариационную
матрицу К, являющуюся
матричным аналогом дисперсии одной
переменной:

где
элементы Кij
— ковариации (или
корреляционные
моменты) оценок
параметров. Ковариация двух переменных
определяется как математическое ожидание
произведения отклонений этих переменных
от их математических ожиданий (см. §
5.6).
Поэтому
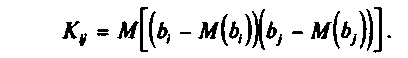
Ковариация характеризует как степень
рассеяния значений двух переменных
относительно их математических ожиданий,
так и взаимосвязь этих переменных.
В
силу того, что оценки ^
, полученные
методом наименьших квадратов, являются
несмещенными оценками параметров Р;,
т.е. М(Ь\
= р
, выражение (33) примет вид:
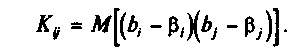
Рассматривая
ковариационную матрицу К,
легко
заметить, что на ее главной диагонали
находятся дисперсии оценок параметров
регрессии, ибо

В
сокращенном виде ковариационная матрица
К
имеет
вид (в этом легко убедиться, перемножив
векторы (Ь
- р)
и (Ь
- р)
.
Учитывая (32),
преобразуем это выражение:
Следовательно,
в силу (35) ковариационная матрица
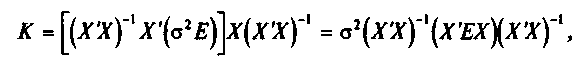

Итак,
с
помощью обратной матрицы (Х'Х} определяется
не только сам вектор σ оценок параметров
(28),
но
и дисперсии и ковариации его элементов.