ТЕМА №7
Многомерный корреляционно-регрессионный анализ. Лекция№1 понятие о многомерном корреляционном анализе.
План: 1. Основные положения корреляционного анализа. Двумерная модель
2. Проверка значимости и интервальная оценка параметров связи
3. Корреляционное отношение и индекс корреляции
4. Понятие о многомерном корреляционном анализе.
1. Основные положения корреляционного анализа. Двумерная модель
Корреляционный анализ (корреляционная модель) — метод, применяемый тогда, когда данные наблюдений или эксперимента можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону.
Основная задача корреляционного анализа, как отмечено выше, состоит в выявлении связи между случайными переменными путем точечной и интервальной оценок различных (парных, множественных, частных) коэффициентов корреляции. Дополнительная задача корреляционного анализа (являющаяся основной в регрессионном анализе) заключается в оценке уравнений регрессии одной переменной по другой.
Рассмотрим простейшую модель корреляционного анализа — двумерную. Плотность совместного нормального распределения двух переменных Х У имеет вид (см. § 5.7):
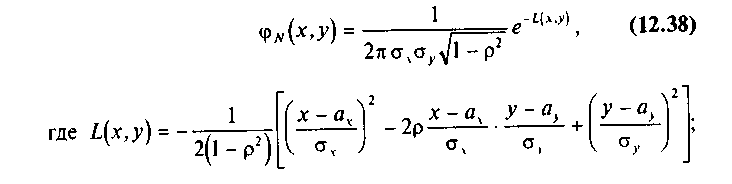
а — математические ожидания переменных X и V;
.σi........— дисперсии переменных Х и V;
ρ — коэффициент корреляции между переменными X и У, или генеральный коэффициент корреляции, определяемый через корреляционный момент (ковариацию) Кху по формуле (5.38):
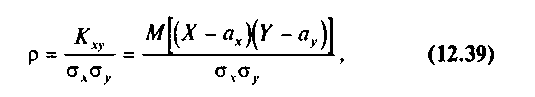
или с учетом (5.40)
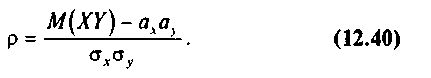
Величина ρ характеризует тесноту связи между случайными переменными X и У в генеральной совокупности. Указанные пять параметров дают исчерпывающие сведения о корреляционной зависимости между переменными.
Из свойств коэффициента корреляции следует, что ρ является показателем тесноты связи лишь в случае линейной зависимости (линейной регрессии) между двумя переменными, получаемой, в частности, в соответствии с (12.41), (12.42) при их совместном нормальном распределении.
Для оценки генерального коэффициента корреляции ρ и модельных уравнений регрессии по выборке в формулах (12.40)—(12.42) необходимо заменить параметры Кху их состоятельными выборочными оценками — соответственно х, у (12.12), а2, (12.18), а2у (12.22), ц (12.19). В этом случае получим формулы для определения выборочного коэффициента корреляции г и выборочных уравнений регрессии.
2. Проверка значимости и интервальная оценка параметров связи
В практических исследованиях о тесноте корреляционной зависимости между рассматриваемыми переменными судят фактически не по величине генерального коэффициента корреляции р (который обычно неизвестен), а по величине его выборочного аналога г. Так как г вычисляется по значениям переменных, случайно попавшим в выборку из генеральной совокупности, то в отличие от параметра р параметр г — величина случайная.
Пусть вычисленное значение г = 0. Возникает вопрос, объясняется ли это действительно существующей линейной корреляционной связью между переменными X и V в генеральной совокупности или является следствием случайности отбора переменных в выборку.
Обычно в этих случаях проверяется гипотеза Но об отсутствии линейной корреляционной связи между переменными в генеральной совокупности, т.е. Я0: ρ = 0. При справедливости этой гипотезы статистика
имеет t-распределение Стьюдента с n = п~1 степенями свободы. Поэтому гипотеза Hо отвергается, т.е. выборочный коэффициент корреляции г значимо (существенно) отличается от нуля, если
