34,. Производная сложной функции

Сложная функция имеет вид: F(x) = f(g(x)), т.е. является функцией от функции. Например, y = sin2x, y = ln(x2+2x) и т.д.

Если в точке х функция g(x) производную g'(x) , а в точке u = g(x) функция f(u) имеет производную f'(u), то производная сложной функции f(g(x)) в точке х существует и равна f'(u)g'(x).

35)Производная степенной функции

Если f(x) = xp, где p - действительное число, то

Если показатель степени является отрицательным числом, т.е. f(x) = x−p, то

36)Производная неявной функции

Во многих задачах функция y(x) задана невным образом. Например, для приведенных ниже функций

невозможно получить зависимость y(x) в явном виде.

Алгоритм вычисления производной y'(x) от неявной функции выглядит следующим образом:

-Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;

-Решить полученное уравнение относительно производной y'(x).

Рассмотрим для иллюстрации несколько примеров.

Пример 1

Продифференцировать функцию y(x), заданную уравнением .

Решение.

Продифференцируем обе части уравнения по переменной x:

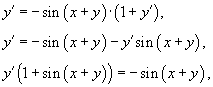
что приводит к результату

3 7 Производные высших порядков.

Df: Пусть ф-ия дифф. на Х , то есть дифф. в каждой т. Х .

Каждому значению Х соответствует единственное значение , т.е. получаем как ф-ию, заданную на Х. Если она окажется дифф. на Х, то мы можем вычислить следующую , которая будет называться второй и т.д.

Df: Производной n-го порядка от ф-ии называется первая производная от производной n-1 порядка.

38 ,39Дифференциал ф-ции и его геометрический смысл. Применение дифференциала к приближённым вычислениям. Если функция y=f(x) имеет производную f '(x) в точке x, то произведение производной f '(x) на приращение Δx аргумента называют дифференциалом функции и обозначают: dy = f '(x)·Δx Дифференциалом ф-ции наз. величина, пропорциональная приращению аргумента х и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем х. Если y=x, то dy=dx=x`x=x, dx=x Если yx, то dy=y`dx, y`=dy,dx Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x0,f(x0)) при изменении x0 на величину x 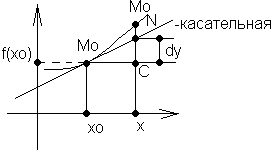Пусть нам известно значение

функции y0=f(x0) и ее производной y0' = f '(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x. Как мы уже выяснили приращение функции Δy можно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x0)·Δx. Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f'(x0)·Δx. Откуда f(x) ≈ f(x0) + f'(x0)·Δx

40,41,43. Теорема Лагранжа, Роля,Ферма. Теорема Лагранжа. Если функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема в каждой внутренней его точке, то внутри отрезка [a;b] найдется такая точка , что выполняется равенство f(b)-f(a)=f ‘()(b-a). Геометрический смысл теоремы Лагранжа.

Если функция y=f(x) на отрезке [a;b] удовлетворяет всем условиям теоремы Лагранжа, то на дуге, являющейся графиком этой функции, найдется такая точка, касательная в которой будет параллельна хорде, стягивающей эту дугу.

Теорема Ролля. Если функция y=f(x) непрерывна на отрезке [a;b], дифференцируема в каждой внутренней точке этого отрезка и на его концах обращается в нуль, то внутри отрезка [a;b] найдется такая точка , что f ‘()=0. Геометрический смысл теоремы Ролля. Если функция y=f(x) удовлетворяет на отрезке [a;b] всем условиям теоремы Ролля, то на графике функции найдется такая точка, касательная в которой параллельна оси абсцисс.

Теорема Ферма: Если ф-я дифференцируема в т. Х0 и принимает в этой точнее минимальное или максимальное значение, то производная в этой точке = 0.

Доказательство: d(X0) = 0 max f (x) = 0 Пусть у = f (x), диф-ся в т. Х0 прим. в этой точке min значение, когда f (X0 + ∆X) ≥ f (X0) Величина ∆у = f (X0 + ∆X) - f (X0) ≥ 0