20.Понятие ф-ии. Способы задания ф-ии

Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.

Переменная х- независимая переменная или аргумент. Переменная у- зависимая переменная

Значение функции- значение у, соответствующее заданному значению х.

Область определения функции- все значения, которые принимает независимая переменная. Область значений функции (множество значений)- все значения, которыепринимает функция.

Способы задания функции

- Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции.Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)-некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.- На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.

№21.Область определения функции.Четность и монотонность.

Область определения функции — это множество допустимых значений аргумента функции. Она обозначается как D(y), когда нужно указать область определения функции y = f(x).

Монотонность: Ф-я у=f(x) назв. Возрастающей на обл.определения D, если для любых х1 Є D, х2Є D и таких, что х2>х1- выполняется соотношение f(x2)>f(x1); Ф-я у=f(x) назв. Убывающей на обл. определения D, если для любых х1 Є D, х2Є D и таких, что х2<х1- выполняется соотношение f(x2)<f(x1);

Четность . ф-я у=f(x) назв. четной если для любых х Є обл.опред-я выполняется соотношение f(-x)=f(x); ф-я у=f(x) назв. нечётной если для любых х Є обл.опред-я выполняется соотношение f(-x)=-f(x).Ф-я которая не является нечетной/четной назв – ф-ей общего вида

№22.Понятие предела. Бесконечно малые величины, их свойства

Предел — одно из основных понятий математического анализа. Различают предел последовательности и предел функции.

Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера.

Предел функцииФункция f(x) имеет предел A в точке x₀, если для всех значений x, достаточно близких к x₀, значение f(x) близко к A.

Бесконечно малая величина

Ф-я у=L(x) назв бесконечно малой ф-й если при х→х0(∞) предел этой ф-и=0

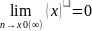
Теорема.Если предел ф-и f(x) при х→х0(∞)=некоторому числу А, то f(x)= А+L(x), где L(x)-бесконечно малая ф-я при х→х0(∞)

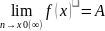, то f(x)= )= А+L(x)

Cв-ва бесконечно малых ф-й(БМФ)

1.Сумма БМФ есть бесконечно малая ф-я

2.Произведение БМФ на постоянную величину есть БМФ

3.произведение БМФ на ограниченную являестя БМФ

№23. Основные теоремы о пределах

Теорема 1 (свойства предела функции).

1. Если  lim_{x  a}f(x) = A , то найдется окрестность точки a 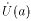такая, что в этой окрестности функция f(x) будет ограничена.

2. Если f(x) есть постоянная A в некоторой окрестности точки a, то lim_{x  a}f(x) = A

3. Если lim_{x  a}f(x) = A₁ и lim_{x  a}f(x) = A₂, то A₁ = A₂

Утверждения данной теоремы вытекают из определения предела функции.

Теорема 2 (арифметические операции над пределами). Если lim_{x  a}f(x) = A, lim_{x  a}g(x) = B, то

1. lim_{x  a}[f(x) g(x)]=A B,

2. lim_{x  a}f(x)g(x) = AB

3. lim_{x  a}f(x)/g(x) = A/B, B  0

Эта теорема непосредственно следует из соответствующей теоремы о пределах последовательностей.

Теорема 3 (предел и неравенства). Пусть f:E R, g:E R, h:E R

1. Если lim_{x  a}f(x) = A, lim_{x  a}g(x) = B и A<B, то  :  x  f(x)<g(x).

2. Если для  x  E f(x)  g(x)  h(x) и существует lim_{x  a}f(x) = lim_{x  a}h(x) = A. то существует lim_{x  a}g(x) = A

Теорема 4 (свойства бесконечно малых функций).

1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая.

3. Произведение конечного числа бесконечно малых является бесконечно малой.

Теорема 5 (Критерий Коши). . Для того, чтобы существовал предел функции f(x) в точке a ( lim_{x  a}f(x) = A ) необходимо и достаточно, чтобы f(x) удовлетворяла в точке a условию Коши.

Аналогично формулируется условие Коши и доказывается критерий Коши и для случаев правого(левого) пределов в точке a, предела при x().

Теорема 6 (существование предела у монотонной функции). Для того чтобы неубывающая на множестве E функция f:E R имела предел при x s, необходимо и достаточно, чтобы она была ограничена сверху, а для того чтобы она имела предел при x i необходимо и достаточно, чтобы она была ограничена снизу.

Теорема 7. Пусть f(x)~ f₁(x), g(x)~ g₁(x) при x a Тогда если существует предел

lim_{x a}f₁(x)/g₁(x),то существует lim_{x a}f(x)/g(x),причем lim_{x a}f₁(x)/g₁(x) = lim_{x a}f(x)/g(x).

Теорема 8. Для того, чтобы функции f(x), g(x) были эквивалентными при x a необходимо и достаточно, чтобы при x a выполнялось хотя бы одно из условий

f(x) = g(x)+o(g(x)) или g(x) = f(x)+o(f(x)).

Заметим, что функции g(x) в первом условии и соответственно функция f(x) во втором называются главной частью функции f(x) (g(x)).

№24Виды неопределенности, их раскрытие

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа(виды):∞-∞, ∞/∞, 0/0,0^0,

1^∞, ∞^0,0*∞

При решении примеров, обычно неопределенности заключают в [].

Неопред-сти такого вида([0*∞])[0/0][∞/∞] раскрывают, используя правило сокращения дробей на множитель создающий неопред-сть.

Для раскрытия неопределённостей видов , , пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

Также используют правило Лопиталя

№25. Первый земечательный предел