3.2.Способы генерации случайных чисел в имитационном моделировании.

Реализуются в модели случайных входов, моделируемых случайных характеристик событий, являются основными при построении имитационных алгоритмов. Независимо от способа генерации необходимо, чтобы выполнялись следующие условия:

1. равновероятность появления любого случайного числа из интервала [0,1];

2. статистическая независимость случайных чисел.

1 способ – использование встроенных функций языков имитационного моделирования или языков общего назначения.

2 способ – взаимосвязь статистических распределений. Из теории вероятности известно, что если частота наступления событий подчиняется распределению Пуассона, то время между наступлениями событий подчиняется экспоненциальному событию. Следовательно, для того, чтобы получить выборку соответствующую распределению Пуассона со средним значением t, необходимо получить столько выборок, соответствующих экспоненциальному распределению со средним значением , сколько требуется для того, чтобы сумма экспоненциально распределенных случайных величин в первый раз превысила бы t.

1) Расчеты основаны на таблице случайных чисел. Можно выбирать с любого числа в любом направлении, но обязательно подряд. Для экспоненциального распределения время , где R-случайное число.

2) Преобразование равномерно распределенной случайной величины с помощью центральной теоремы теории вероятности – сумма большого числа n-независимых одинаково равномерно распределенных случайных величин в интервале [0;1] асимптатически приближается к нормальному распределению при n→∞. Случайные числа R1,R2,…Rn, величина ; Среднее значение ; , где величина T ассимптотически нормальная величина. Нормально достигается при . Если необходимо смоделировать нормальный закон распределения со средними значениями и , то случайное отклонение y соответствующие указанному объему выборки n получается из (выражают y) => при n=12, где -выбираем из таблицы случайных чисел.

3) Аппроксимация (замена) непрерывной функции р(х) дискретной функцией распределения. Множество значений случайных величин разбивается на интервалы.

А) частотное распределение Б) эмпирическое распределение

h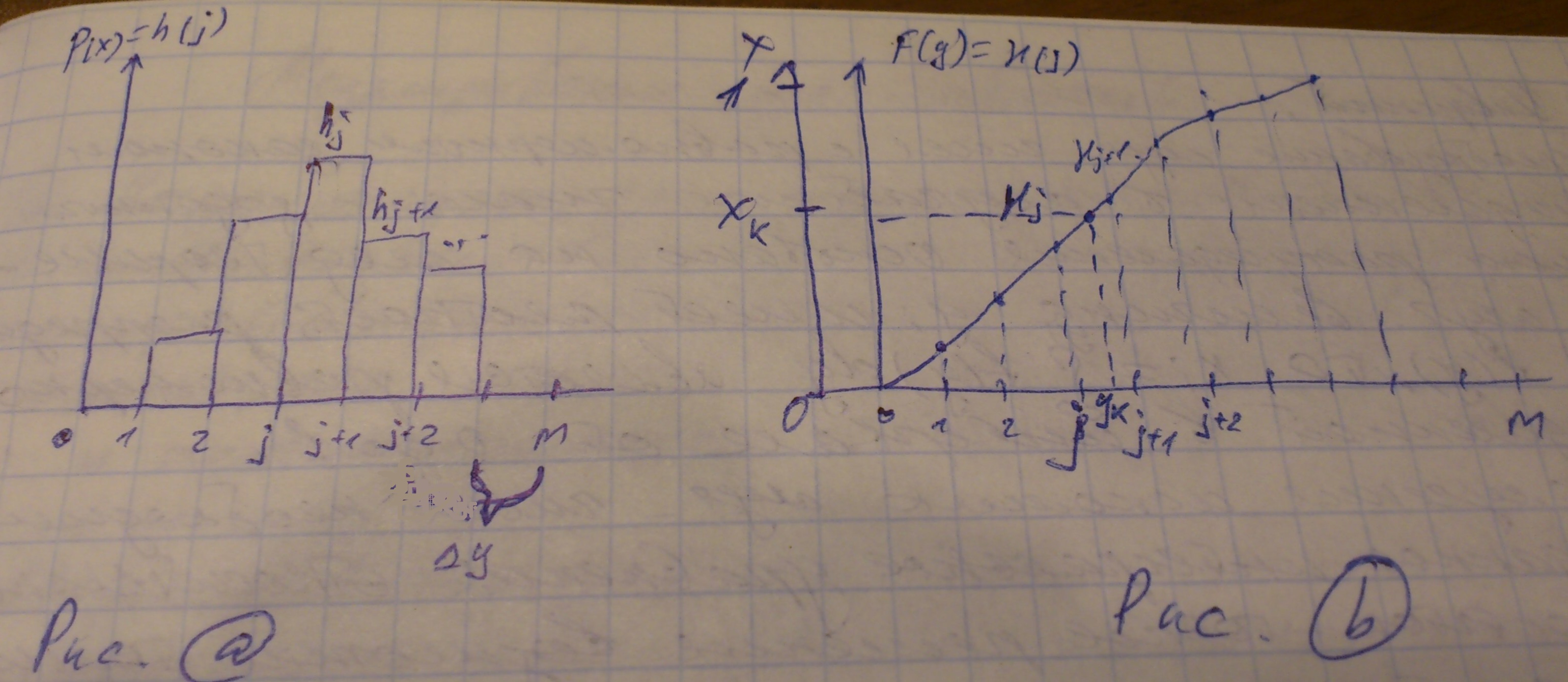 j – частота попадания случайного фактора У в j-й интервал, Уi – значение случайного фактора, соответствующего крайней правой точки j-го интервала, ∆У – шаг интервала. -накопленная частота попадания случайного фактора У в интервал [0;Yi]. Для равных интервалов: Уi=j*∆У.

Для получения случайного числа Ук с заданным законом распределения надо, получая случайные числа Хк, равномерно распределенные от 0 до 1, проверять, начиная с j=1, следующее условие: . Если это неравенство не выполняется, то j =j+1. Иначе Ук определяется по формуле: .

4) Инверсный способ. Преобразование случайных чисел с равномерным законом распределения в случайные числа с заданным законом распределения основано на следующей теореме: если случайная величина y_i имеет плотность распределения f(y), то случайная величина , то x_i является равномерно распределенной в интервале [0,1]. Для получения искомых случайных чисел необходимо решить данное интегральное уравнение относительно y_i, точное решение возможно только для относительно простых распределений, а именно:

а) равномерное распределение на интервале [a;b]:

б) показательное(экспоненциальное) распределение: p(x)=μ*e^-μx, μ=const.

Надо доказать, что случайное число рассчитывается по формулам:

а)Xi=Yi(b-a)+a; б) Xi=-ln(Yi)/μi.

Для а)

Для б)