3.1.Имитационное моделирование как эксперимент. Метод Монте-Карло.

Основная идея данного метода состоит в использовании выборки случайных чисел для получения искомых оценок.

Для демонстрации метода Монте – Карло рассмотрим следующий пример. В этом примере особо подчеркнута статистическая природа имитационного эксперимента.

Используем метод Монте – Карло для оценки площади круга, уравнение окружности которого имеет вид: . Круг имеет радиус r=5 см, и его центр находится в точке (х,у) =(1,2).

Процедура оценки площади требует заключение круга в описанный около него квадрат, сторона которого равна диаметру круга (рисунок 1). Вершины квадрата определяются непосредственно из геометрических свойств фигуры.

О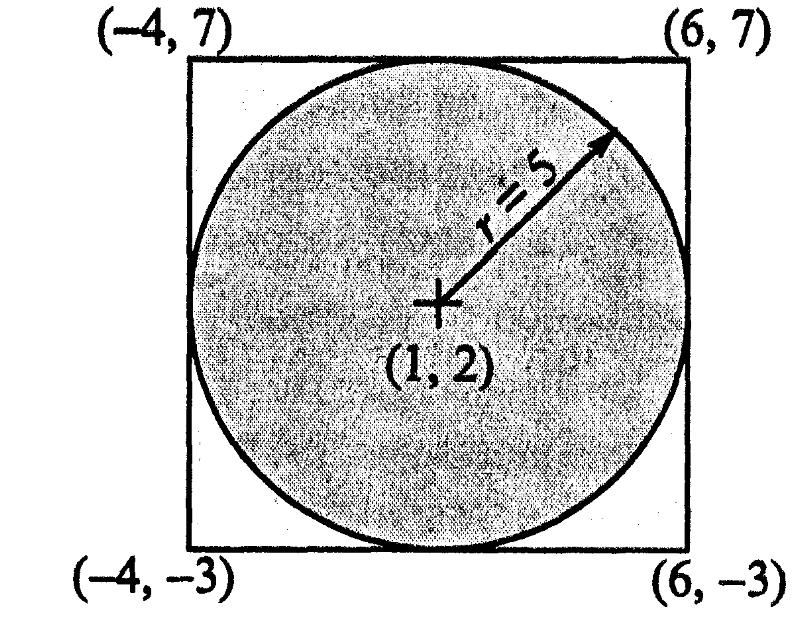 ценка площади круга основана на предположении, что все точки квадрата равновероятны. Предположим, что выборка состоит из наблюдений n точек квадрата и m из них попали внутрь круга или на окружность. Тогда .

Здесь координаты х и у точек квадрата представлены как равномерно распределенные случайные величины с плотностями вероятностей:

, .

Обе функции равны нулю вне указанных интервалов.

Пусть и - различные случайные числа из интервала [0,1]. Тогда координаты (х,у) точек квадрата можно выразить через эти случайные числа:

и .

Используя приведенные формулы, мы можем сгенерировать равномерно распределенную случайную точку (х, у) квадрата для каждой пары случайных чисел ( , ). Сгенерированная точка попадает внутрь круга, если . Например, если =0,0589 и =0,6733, то

,

Так как величина меньше 25, следовательно, точка попадает внутрь круга.

Исследуем теперь влияние случайной выборки на точность оценки площади круга для различных объемов выборки, изменяющихся от n=100 до n=10000. При каждом n эксперимент повторялся 10 раз, при этом исследовались различные последовательности случайных чисел в интервале [0,1].

Исходя из результатов эксперимента, можно сделать следующие выводы:

1. Оценка площади круга улучшается с увеличением объема выборки.

2. Усреднение результатов 10 прогонов для каждой выборки объемом n дает более точную оценку площади, чем любой из прогонов.

3. Уменьшение величины стандартного отклонения свидетельствует о том, что «точность» среднего 10 экспериментов повышается с увеличением объема выборки n.

Ввиду того, что оценки площади имеют разброс, важно, чтобы результаты эксперимента, связанного с моделированием, были выражены в виде доверительных интервалов, показывающих величину отклонения от точного значения. В рассматриваемом пример, если А представляет собой точное значение площади, а и - среднее и дисперсию N наблюдений, то % - й интервал для А задается в виде , где - %-я точка t – распределения (распределения Стьюдента) с N – 1 степенями свободы (n – объем выборки). В рассматриваемом примере мы заинтересованы в установлении доверительного интервала, полученного для выборки наибольшего объема (т.е. n=10000). При N =10, =78.57 и s=0.47 , результирующим 95%-м доверительным интервалом является .

Рассмотренный пример ставит 2 вопроса, характерные для любого эксперимента, связанного с моделированием:

1. Каким должен быть объем выборки n для достижения необходимого значения доверительных интервалов?

2. Сколько для этого требуется прогонов N?

Ответы зависят от природы эксперимента, связанного с моделированием. Как и в любом статистическом эксперименте, большие значения n и N обеспечивают более надежные результаты. Препятствием может быть стоимость проведения эксперимента, которая возрастает пропорционально увеличению n и N.