6.5.Системы массового обслуживания ограниченной мощности.

Для модели (М/М/1):(GD/N/∞) используются следующие формулы расчета параметров:

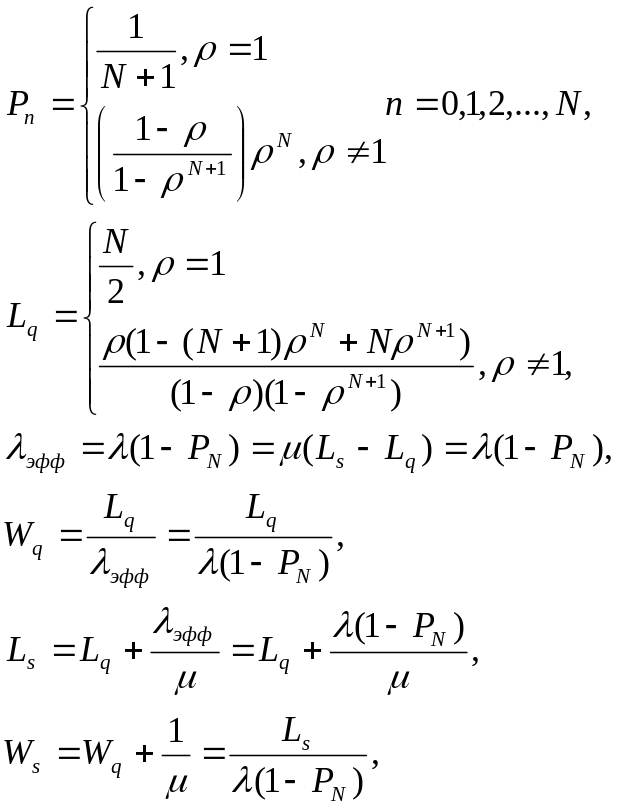
где - вероятность того, что требование не может присоединиться к очереди;

- эффективная частота, которая учитывает действительно допускаемые в систему требования в единицу времени.

Параметр определяется: ;

Для модели (М/М/c):(GD/N/∞) используются следующие формулы расчета параметров:

где - среднее количество «простаивающих» обслуживающих узлов, а

.

Кроме того целесообразно рассчитать коэффициент загруженности системы по формуле .

6.6.Влияние числа узлов обслуживания на основные операционные характеристики системы массового обслуживания.

Уменьшить среднюю продолжительность нахождения прибывших заявок в очереди можно, если увеличить число обслуживающих узлов. Проанализируем, как повлияет это мероприятие на изменение продолжительности ожидания заявок в очереди:

1. Увеличивается количество обслуженных заявок;

2. Уменьшается средняя длина очереди, а так же среднее время ожидания в очереди;

3. Уменьшается длина очереди.

Проанализируем, как повлияет это мероприятие на обслуживающие узлы:

1. Соответственно увеличивается емкость обслуживающих узлов;

2. Увеличивается количество занятых устройств;

3. Увеличивается коэффициент использования.

Увеличение количества обслуживающих устройств может как и улучшить работу модели так и ухудшить, следовательно, если при увеличении обслуживающих узлов появляются отрицательные характеристики следует уменьшить число обслуживающих устройств.

6.7.Системы массового обслуживания с приоритетами.

Предполагается, что у входа в блок обслуживания формируются несколько очередей, в каждой из которых заявки имеют различные уровни предпочтения. Считается что первая очередь – обладает наивысшим приоритетом, а последняя – самым низким приоритетом. Частоты поступления заявок и продолжительность их обслуживания неодинаковы. Дисциплина очереди – ПЕРППО. Обслуживание может осуществляться по одному из правил:

1. правило прерывания – начатое обслуживание может прекращаться при поступлении заявки с более высоким приоритетом.

2. правило без прерывания (NPRP) – начатая процедура обслуживания доводится до конца даже если поступает заявка с высшим приоритетом.

Рассматриваются одноканальные и многоканальные модели. В первом случае входной поток является Пуассоновским, а распределение продолжительности обслуживания произвольного вида. Во втором случае входные и выходные потоки – Пуассовонские.

а) Одноканальные системы .

- произвольная функция распределения продолжительности обслуживания из i-ой очереди со средней величиной и дисперсией . Для произвольной очереди:

;

;

;

;

;

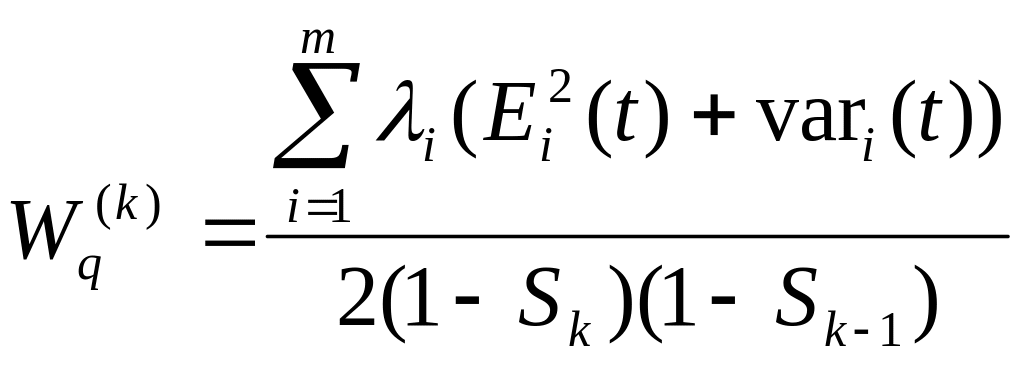где k=1…m; S₀=0.

Среднее время пребывания клиента в очереди не зависит от приоритета, к-ым он обладает.

, где ;

б) Многоканальные системы .

Для производной очереди:

; где S₀=0;