1. Принцип двойственности

Функция , равная , называется двойственной функцией к функции .

Очевидно, что таблица истинности для двойственной функции получается из таблицы истинности для функции инвертированием (т. е. заменой 0 на 1 и 1 на 0) значений переменных и функции. Например, .

Легко установить для функций 0, 1, , , , , что

1. функция 0 двойственна 1;

2. функция 1 двойственна 0;

3. функция двойственна ;

4. функция двойственна ;

5. функция двойственна ;

6. функция двойственна.

Из определения двойственности следует, что

,

т. е. функция является двойственной к (свойство взаимности).

Принцип двойственности. Если формула реализует функцию , то формула , т. е. формула, полученная из заменой функций соответственно на , реализует функцию .

Формулу будем называть формулой, двойственной к .

Для доказательства этого утверждения необходимо проверить его справедливость для элементарных шагов суперпозиции и .

Пусть, например, функция получается из функции в результате следующей подстановки переменных :

.

Тогда

т. е. функция получается из в результате той же самой подстановки переменных.

Доказательство справедливости принципа двойственности для шага проведем на примере. Пусть

.

Тогда

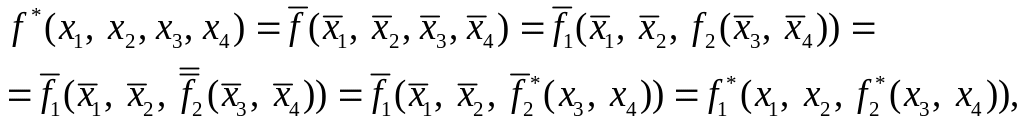
т. е. функция получается из и так же, как функция из и .

Принцип двойственности позволяет упростить вывод основных тавтологий и имеет целый ряд полезных применений, которые будут рассмотрены далее.

Пример 2. Построение формулы для отрицания функции.

Из определения двойственной функции следует

.

Получаем следующее правило: пусть формула реализует функцию . Чтобы получить формулу для функции нужно в формуле заменить все переменные на их отрицания.

Найдем отрицание для функции .

Так как , то .

6

2. Разложение булевых функций по переменным. Совершенные

дизъюнктивная и конъюнктивная нормальные формы

Введем обозначение

,

где – параметр, равный либо 0, либо 1. Очевидно, что

Легко видеть, что 1 тогда и только тогда, когда .

Теорема о разложении функций по переменным. Каждую функцию алгебры логики при любом ( ) можно представить в следующей форме:

, (1)

где дизъюнкция берется по всевозможным наборам значений переменных .

Это представление называется разложением функции по переменным .

Доказательство. Рассмотрим произвольный набор значений переменных и покажем, что левая и правая части соотношения (1) принимают на нем одно и то же значение. Левая часть дает . Правая –

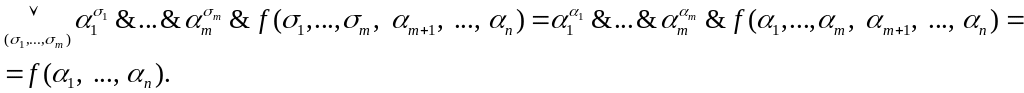
В качестве следствий из теоремы рассмотрим два специальных случая разложения.

1. Разложение по переменной:

.

Функции и называются компонентами разложения. Данное разложение полезно, когда какие-либо свойства устанавливаются по индукции.

2. Разложение по всем переменным:

.

При тождественно не равной 0 оно может быть преобразовано:

.

В результате окончательно получим

. (2)

Такое разложение называется совершенной дизъюнктивной нормальной формой (совершенной д. н. ф.).

Непосредственно к понятию совершенной д. н. ф. примыкает следующая теорема.

Теорема. Каждая функция алгебры логики может быть представлена формулой в базисе .

Доказательство.1) Пусть . Тогда, очевидно,

.

2. Пусть тождественно не равна 0. Тогда ее можно представить формулой (2).

Данная теорема носит конструктивный характер, так как она позволяет для каждой функции построить реализующую ее формулу в виде совершенной д. н. ф. Для этого в таблице истинности для каждой для функции отмечаем все строки , в которых . Для каждой такой строки образуем логическое произведение , а затем все полученные конъюнкции соединим знаком дизъюнкции.

Пример 3. Найти совершенную д. н. ф. для функции .

Совершенная д. н. ф. есть выражение типа П. Покажем, что при тождественно не равной 1 ее можно представить в виде . Запишем для двойственной функции (очевидно не равной тождественно 0) разложение в виде совершенной д. н. ф.:

.

Из принципа двойственности следует

.

Таким образом, получаем разложение, которое называется совершенной конъюнктивной нормальной формой (совершенной к. н. ф.):

. (3)

Пример 4. Построить совершенную к. н. ф. для функции .

Имеем .

7