27 Синтез схем дешифратора
Общая теория синтеза СФЭ приводит к
выводу о том, что большинство булевых
функций
при больших значениях
имеет сложные минимальные схемы. Это
означает, что практическую ценность с
точки зрения синтеза представляет
весьма узкий класс булевых функций.
Поэтому наряду с универсальными методами
синтеза необходимо иметь методы синтеза,
приспособленные к отдельным классам
булевых функций, полнее учитывающие
свойства отдельных функций.
Рассмотрим далее две многополюсные схемы, имеющиеся в каждом компьютере.
Дешифратором называется схема,
имеющая
входов
и
выходов, на которых реализуются
всевозможные элементарные конъюнкции
ранга
.
Условное обозначение такой схемы для
приведено на рис. 8
При подаче на входы дешифратора какой-либо комбинации нулей и единиц еди-
ничный сигнал появляется только на одном из выходов,
остальные выходы находятся в нулевом состоянии.
В ЭВМ дешифратор применяется для записи или
считывания информации из памяти: на вход подается
двоичный адрес определенной ячейки памяти, это
вызывает появление единичного сигнала ровно на одном из выходов, который связан с соответствующей ячейкой, что приводит к операции считывания-записи именно для этой ячейки.
Схему дешифратора можно построить
индуктивно, добавляя для каждого входа
блок из
(
)
конъюнкторов. Построенная таким образом
схема дешифратора для
показана на рис. 9.
28. Синтез схемы двоичного сумматора.
Двоичный сумматор – это схема,
реализующая сложение двух целых чисел,
заданных в двоичной системе счисления:
,
.
Условное обозначение схемы сумматора показано на рис. 10.
Рассмотрим хорошо известный алгоритм
сложения чисел
и
«столбиком»:
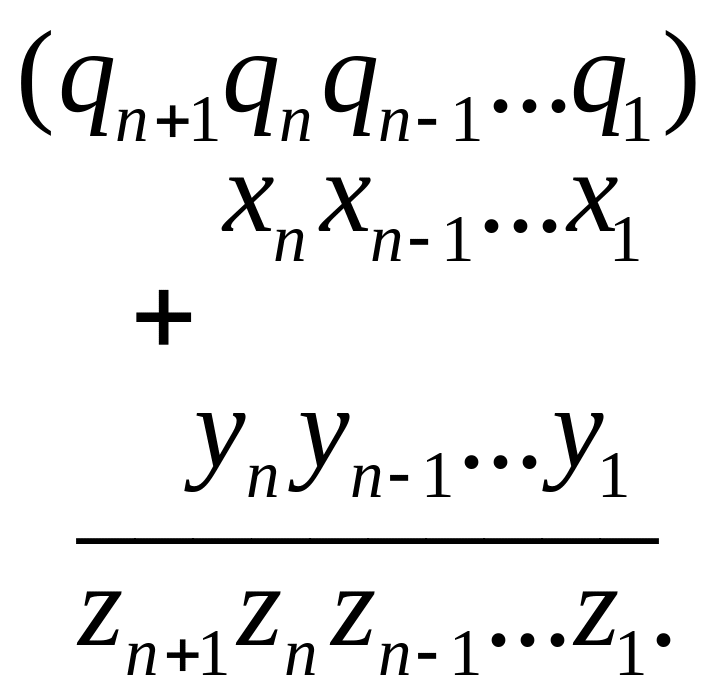
Здесь числа
обозначают результаты переносов из
предыдущих разрядов
.
Очевидно,
,
.
Основываясь на тождестве
,
получаем схему, реализующую соответствующее
преобразование величин
в
(рис. 11).
Обозначим эту схему через
(
).
Тогда искомая схема
получается путем
последовательного соединения блоков (рис. 12).
Здесь
,
и блок
осуществляет преобразование
,
.
Очевидно,
и
при
.
Таким образом,
.
29. Определение и способы задания конечного автомата
СФЭ не учитывают тот факт, что реальные устройства работают во времени. По сравнению с СФЭ конечный автомат является более точной моделью дискретного преобразователя информации. При этом понятие конечного автомата, как и любая модель, связано с рядом упрощающих предположений.
Во-первых, предполагается, что вход и выход автомата в каждый момент времени может находиться только в одном из конечного числа различных состояний. Если реальный преобразователь имеет непрерывный входной сигнал, то для его описания с помощью конечного автомата необходимо провести квантование этого сигнала. В формальном определении автомата конечный набор состояний входа и выхода автомата называется соответственно входным и выходным алфавитом, а отдельные состояния – буквами этих алфавитов.
Во-вторых, предполагается, что время
изменяется дискретно. Состояния входа
и выхода соответствуют дискретной
временной последовательности
Поскольку момент времени однозначно
определяется его индексом, то с целью
упрощения будем считать, что время
принимает значения 1, 2, …,
,
… Временной промежуток
называется тактом.
Работа автомата представляется следующим образом.
На вход автомата поступают сигналы
из
входного алфавита
,
что приводит к появлению сигналов на
выходе
из входного алфавита
.
Зависимость выходной последовательности
от входной зависит от внутреннего
устройства автомата. Заметим, что в
отличие от СФЭ, которые не обладают
памятью, автомат представляет собой
устройство с памятью, т. е. выход автомата
определяется не только входом
,
но и предысторией
.
Учет предыстории осуществляется
зависимостью выходного сигнала не
только от входа, но и от текущего
состояния, которое обозначим
.
Дадим формальное определение автомата.
Конечным автоматом называют пятерку объектов
,
(1)
где
– конечное множество, называемое входным алфавитом; – одно из возможных состояний входа;
– конечное множество, называемое
выходным алфавитом; элементы этого
множества определяют возможные состояния
выхода;
– конечное множество, называемое
алфавитом внутренних состояний;
– функция переходов автомата:
;
эта функция каждой паре «вход-состояние»
ставит в соответствие состояние;
– функция выходов автомата:
;
эта функция каждой паре «вход-состояние»
ставит в соответствие значение выхода.
Закон функционирования автомата: автомат изменяет свои состояния в соответствии с функцией и вырабатывает выходные сигналы в соответствии с функцией :
,
,
