10. Комплексные сигналы. Методы формирования, примеры и цели использования комплексных сигналов в системах передачи данных.

В природе комплексных сигналов не существует, только вещественные – различные физические величины, изменяющиеся во времени. В нашем случае – напряжение, ток, напряженность электрического поля. В математической модели можно создать функцию сигнала.

Вещественный сигнал перемещается вдоль вещественной оси. К.с. – добавляется перемещение вдоль мнимой оси. В любой момент времени может быть решен вопрос о выделении информативной части сигнала.

Получение функции по мнимой оси – преобразование Гильберта: К.с. – аналитический сигнал - - перемещение по окружности против хода часовой стрелки, поскольку идет запаздывание синуса по отношению к косинусу.

- комплексная экспонента.

Такой сигнал не несет информации. Необходимо изменение А(t) и ф(t).

Изменение A(t) – изменение формы окружности, изменение ф(t) – ускорение (замедление) (скорость = постоянная составляющая + изменяющаяся).

Постоянная составляющая w₀t информации не несет, для выделения информации из сигнала, постоянную составляющую нужно убрать.

Переход к к.о. - .

А.с. – передается по каналам связи, преобразование – получение информации (фиксирование точки на окружности, перемещение точки по прямой (А) или по дуге (ф)). Сигнал вычисляется с задержкой Т/2.

11. Аналитический сигнал. Огибающая и фаза аналитического сигнала. Представление аналитического сигнала на комплексной плоскости. Спектр аналитического сигнала.

А налитический сигнал образуется из исходного вещественного cигнала путем добавления к нему мнимой части , которая получается преобразованием Гильберта

.

При этом в мнимой части происходит сдвиг фаз всех спектральных составляющих сигнала на –90 градусов, то есть в сторону запаздывания, иначе говоря, косинусоидальные спектральные составляющие сигнала заменяются синусоидальными.

Аналитический сигнал можно представить через огибающую A(t) и полную фазу Ф(t) вещественного сигнала

где

Таким образом, через аналитический сигнал можно найти текущие значения огибающей A(t) и полной фазы Ф(t) вещественного сигнала в любой момент времени, что часто используется на практике для извлечения из сигнала информации.

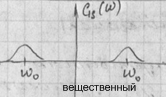
Спектр аналитического сигнала в области положительных частот совпадает с односторонним спектром вещественного сигнала, а в области отрицательных частот тождественно равен нулю.

Полная фаза Ф(t) содержит в себе фазу несущей частоты ₀t, что не совсем удобно для анализа. Поэтому для переноса спектра аналитического сигнала влево по оси частот на -₀ в область модулирующих частот (для удаления несущей), аналитический сигнал умножают на комплексную экспоненту с частотой -₀, равной частоте несущей и получают комплексную огибающую.

Аналитический сигнал зависит от действительного аргумента, является однозначным и дифференцируемым. На комплексной плоскости он отображается вектором, модуль и фазовый угол которого изменяются от аргумента, а проекция сигнала на вещественную ось равна значению исходного сигнала s(t). Какой-либо новой информации аналитический сигнал не несет, так как получен линейным преобразованием из исходного сигнала и представляет собой его новую математическую модель.

Спектр аналитического сигнала:

В отрицательной области частот спектра тождественно равен 0

В положительной области совпадает с односторонним спектром вещественного сигнала