6. Ортогональные и ортонормированные системы базисных функций. Широкораспространенные системы базисных функций.

Бесконечная система функций называется ортогональной на отрезке от a до b если Где n<>m и при этом

Два сигнала называются ортогональными, если их скалярное произведение, а значит, и взаимная энергия равна нулю.(интеграл от их произведения). Пусть Н – гильбертово пространство сигналов с конечным значением энергии. Эти сигналы определены на отрезке времени [t1;t2], конечном или бесконечном. Предположим, что на этом же отрезке задана бесконечная система функций {u0, u1… un…}, ортогональных друг другу и обладающих единичными нормами:

Говорят, что при этом в пространстве сигналов задан ортонормированный базис.

Примеры ортонормированных базисов. Рассмотрим две наиболее важные и распространенные системы.

Ортонормированная система гармонических функций. На отрезке [0,T] система тригонометрических функций с кратными частотами , дополненная постоянным сигналом.

U₀=1/

U₁=

U₂=

……………………………………..

U_2m-1=

U_2m=

Образует ортонормированный базис

Ортонормированная система функций Уолша

Функции Уолша представляют собой полную систему ортогональных, ортонормированных функций. Обозначение: wal(n, Q), где n- номер функции, при этом: n = 0, 1,... N-1; N = 2ⁱ ; i = 1, 2,….

Функции Уолша образуют ортогональную систему, принимающую значения только 1 и −1 на всей области определения.

П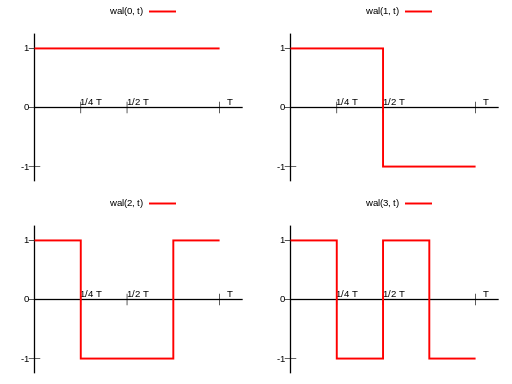 усть функция Уолша определена на интервале [0, T]; за пределами этого интервала функция периодически повторяется. Введём безразмерное время  . Тогда функция Уолша под номером k обозначается как  . Нумерация функций зависит от метода упорядочения функций. Первые 4 функции Уолша.

Свойства

1. Ортогональность

Скалярное произведение  двух разных функций Уолша равно нулю:

2.Мультипликативность

Произведение двух функций Уолша даёт функцию Уолша.

СБФ должна удовлетворять условиям ортогональности и ортонормированности.

Условия ортогональности двух базисных функций заключаются в равенстве нулю их взаимных мощностей

Условия ортонормированности заключаются в равенстве единице мощности всех базисных функций

Любую СБФ можно нормировать, если разделить каждую базисную функцию на ее мощность.

Наиболее часто используются следующие СБФ:

- Системы единичных непрерывных и дискретных функций.

- Системы тригонометрических базисных функций:

- Системы комплексных экспоненциальных функций. Эти функции используются в преобразованиях Фурье и Лапласа.

- Двоично - ортогональные СБФ Уолша, Хаара, Радемахера. Эти функции широко используются в вычислительной технике для анализа и синтеза цифровых автоматов.

7. Корреляционные (временные) характеристики сигналов. Авто- и взаимная корреляционная функции, их свойства.

А вто Корреляционная функция: показывает степень сходства между сигналом и его сдвинутой копией – чем больше значение корреляционной функции, тем это сходство сильнее.

- для сигнала с ограниченной энергией.

- для сигнала с неограниченной энергией.

К орреляционная функция имеет следующие свойства:

1. четная функция:

2. B(0)=E – максимум

3. Если функция периодическая с периодом Т, то КФ так же периодична с периодом Т.

П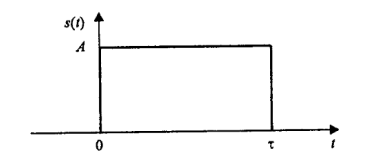 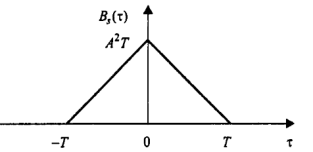ример: КФ для прямоугольного импульса (рис)

В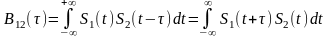 заимная корреляционная функция: показывает степень подобия 2^х разных сигналов.

В заимная Корреляционная функция имеет следующие свойства:

1 .Не является симметричной, но

2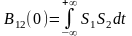 .Значение ВКФ в 0 ничем не выделяется; максимум может быть расположен в любом месте оси .

3.

П ример: ВКФ прямоугольного и треугольного импульсов.