26.Оптимальная линейная фильтрация сигнала. Согласованный фильтр, его импульсная характеристика.

Выделение сигнала из помех является одной из важнейших задач, которые необходимо решить при разработке практически любой системы передачи информации. Данная задача выполняется при помощи линейных фильтров, основанных на частичной избирательности.

О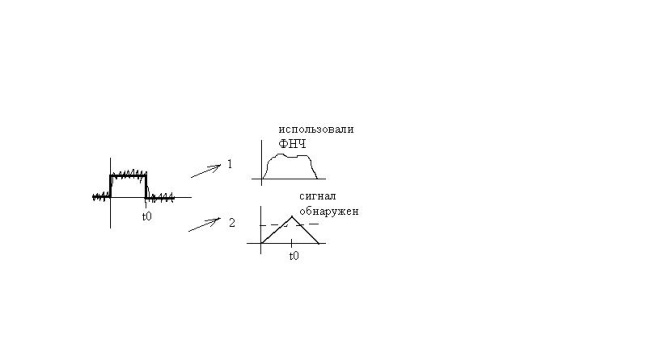 птимальным фильтром называется фильтр, который решает задачу отделения полезного сигнала от шума наилучшим образом с точки зрения выбранного критерия оптимальности.

1 критерий – обнаружение сигнала (в радиолокации)

2 критерий – воспроизведение сигнала (полосовой фильтр АЧХ = 1)

Согласованная фильтрация

Согласованный фильтр – оптимальный фильтр для первого критерия – имеющий АЧХ: K(ω)=kG(ω), где K(ω) – коэф. передачи, k – коэф. пропорц., G(ω) – спектр сигнала, и ФЧХ: - фильтр, согласованный с этим сигналом - фазовый спектр. t₀ - момент t, в котором будет воспроизводится обнаружение сигнала.

Фильтр пропускает на свой выход спектральные составляющие сигнала с коэф. передачи пропорциональным их величине G(ω). Это приводит к увеличению отношения сигнал/шум в вых сигнале. Форма сигнала будет сглажена. Второе условие(φ(ω)) приводит к тому, что в момент времени t₀ все спектральные компоненты вых. сигнала фильтра оказываются с фазированными и их сумма Y_вых = мах

Импульсная характеристика согласованного фильтра – зеркальная копия входного сигнала, сдвинутого вдоль оси t на величину t₀.

g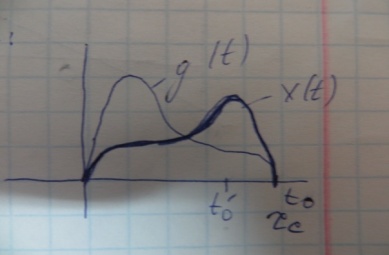 (t) =

27. Устойчивость замкнутых линейных цепей. Условие и критерии устойчивости.

Если цепь представляет собой систему звеньев с ОС, то появляется проблема устойчивости такой системы. Устойчивость – внутреннее свойство замкнутой системы, обеспечивает затухание вых. Сигнала Y(t) при X(t)=0., , при x(t)=0

Причина появления неустойчивости:

- сильная положительная ОС,  раскачивает систему;

- изменение на некоторых частотах знака ОС из-за непостоянства ФЧХ;

Рассмотрим условие устойчивости произвольной линейной системы:

Такая система описана ДУ некоторого порядка:

Q(p)= -характеристическое уравнение системы

Для определения устойчивости нас интересует наличие y(t) при x(t)=0 => ДУ – однородное, а общее решение ДУ (при отсутствии кратных корней).

Решение характерист. ур-ния составляющая  (свободная или переходная составляющая) Поведение свободной составляющей определяется решением однородного дифференциального уравнения

При 0 вх сигнале свойство системы определяется только значением передаточной функции. Ур-е Q(p)=0 характеристическое уравнение системы.

Условие устойчивости – Отрицательное значение вещественных частей всех корней характеристического уравнения ( p_i <0).

Критерии устойчивости:

1)алгебраические- решение характеристического уравнения;-критерий Гурвица

2)геометрические (критерий Михайлова; критерий Найквиста)

1) Критерий Гурвица: ХУ

Для того, чтобы все корни лежали в левой полуплоскости необходимо и дост.:

-

- Определитель Гурвица n-1 порядка >0 (D_n-1>0);

- Все главные миноры определителя Гурвица D_n-2, D_n-3 >0;

; D₁ = 2 > 0; a₃ > 0; a₀ > 0; => Система устойчива.

2) Критерий Михайкова: Рассмотрим ХУ при условии подстановки в него комплексной составляющей:

В этот хар. Полином подставим значения частот ω=0…∞ => кривая:

Система является устойчивой, если при изменении частоты от 0 до +∞ аргумент хар. полин. ↑ на угол не более , где n – ст. ХУ.

3) Критерий Найквиста:

Замкнутая система с ОС будет устойчивой, если коэффициент передачи разомкнутой системы не охватывает точку с координатами (-1;0). в диапазоне частот (-∞;+∞). Строим годограф: