2. Планирование эксперимента при наличии неуправляемого аддитивного дрейфа.
Часто эксперимент приходится проводить в условиях неоднородности типа неуправляемого дрейфа (изменение выходного показателя y во времени или по какой-либо другой координате).
Примерами таких дрейфующих объектов являются каталитические процессы, где выходной y меняется во времени (уменьшается из-за старения катализатора). Другим примером являются тепловые процессы в печах, где происходит изменение теплопередачи из-за постепенного разрушения футеровочного слоя.
Построение зависимости выходного показателя от исследуемых факторов x с помощью обычных планов невозможно, так как получаемые коэффициенты модели будут искажены влиянием указанного дрейфа.
Для
построения линейной модели
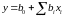по управляемым факторам Джон Бокс
предложил использовать планы типа
табличных полиномов Чебышева. Такие
планы не позволяют оценивать взаимное
влияние факторов и кроме того число
уровней по каждому фактору получается
достаточно большим, сопоставимым с
числом опытов многофакторных планов.
Вместо таких планов, которые строятся
численными методами с учетом специальной
рандомизации, можно использовать
стандартные планы типа двухуровневых
планов
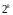выбором из них соответствующих столбцов
для варьирования реальными факторами
в конкретных экспериментах. Такая
возможность основана на связи полиномов
Чебышева со столбцами обычной матрицы
плана
.
Если рассматривать результаты опытов y в многофакторном плане как функцию времени, то эту зависимость f(y,t) можно разложить во временной ряд – ряд Фурье, ряд Чебышева, ряд дискретных функций Уолма, которые соответствуют столбцам матрицы плана .
Полиномы Чебышева связаны с функциями Уолма:
полином I порядка представляет собой сумму первых членов разложения Уолма первых k столбцов для N опытов
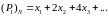
Пример:
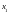
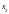
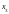
полином Чебышева II порядка для N опытов представлен в виде членов разложения в Уолма соответствует столбцам парных взаимодействий в стандартной матрице плана
полином Чебышева III порядка может быть выражен через сумму столбцов соответствующих взаимодействию 3.
Исходя из указанной связи, можно легко получить следующее правило для получения плана эксперимента с целью построения модели связи показателя y от варьирующих факторов x в условиях неуправляемого дрейфа.
Правило:
Если дрейф предполагается линейным или монотонным для построения указанной модели, коэффициенты которой не будут искажены таким дрейфом, надо расписать матрицу в стандартном виде.
В
этой матрице не надо использовать для
варьирования факторами первые k
столбцов, которые входят в разложение
дрейфа. А реально исследуемые факторы
варьировать согласно оставшимся
столбцам. При этом можно получить модель
,
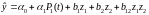включающую как коэффициенты влияния
самих факторов, так и их взаимодействия,
которые не будут искажены дрейфом
.
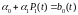Исследовался
процесс синтеза додецилмеркаптана по
полупромышленной установке периодического
действия
.
Цикл работы установки периодического
действия составлял 40ч, после которого
из-за старения катализатора выход
продукции y падал до
минимума при постоянных значениях
основных управляемых факторов
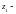температура
давление
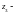скорость
подачи олефина (мл/ч)
скорость
подачи другого реагента
Выходной показатель – годные проценты.
Выгрузка готовой продукции и анализ содержания в ней додецилмеркаптана составлял порядка 5ч.
Для
того чтобы получить модель зависимость
выходного параметра y
от варьируемых факторов z
в условиях такого монотонного падающего
дрейфа на цикле работы установки Т=40ч,
допустимые фиксации каждого опыта в
интервале
можно было поставить 8 опытов. Для
получения указанной зависимости по 8
допустимым опытам был выбран обычный
план
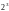из 8 опытов. Поскольку дрейф (изменение
y)
предполагался линейным, для учета такого
дрейфа и исключительно его влияния на
коэффициент дрейфа. Для оценки влияния
каждого из 4 исследуемых факторов z
использовали оставшиеся столбцы
стандартной матрицы
,
т.е. столбцы попарных произведений
первых k=3
столбцов и столбец их тройного
произведения. Причем выбор столбцов
для каждого из факторов z
осуществляется случайным образом
поскольку выбранные для факторов z
столбцы ортогональны первым трем 3
столбцам , представляющим линейный
дрейф, то коэффициенты влияния факторов
z
варьируемых по таким оставшимся столбцам
будут оцениваться независимо от
указанного линейного дрейфа, т.е. не
будут искажены им и могут быть вычислены
по обычным формулам плана
. При этом аналогичным образом легко
вычисляется влияние самого дрейфа и
существенность его влияния на ряду с
влиянием основных факторов.
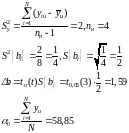
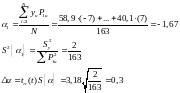
Для проверки адекватности полученной модели с помощью F-критерия Фишера по полученной модели рассчитываем предсказываемые модели значений в каждом из 8 опытов реализованного эксперимента.
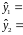
Следующим шагом является вычисление остаточной суммы квадратов, т.е. суммы квадратов разностей наблюдаемых y и предсказываемых значений показателя y в каждом из 8 опытов.
N – число опытов; L – число коэффициентов
Модель адекватно описывает интересующую зависимость в исследуемой области режимов.
Модель была использована в методе крутого восхождения. Существенно, что при реализации многофакторного плана при наличии дрейфового многофакторного плана. Опыты проводят в строго последовательном порядке во времени, поскольку время здесь является одной из переменных, изучаемых одновременно с варьированными факторами.
В связи с этим обычная рандомизация (реализация опытов многофакторных планов в случайном порядке) невозможно.
Рандомизацию условий эксперимента в этом случае осуществляют путем случайного распределения реально варьируемых факторов (в нашем примере z) по столбцам, оставшимся матрицы плана (без использования первых k столбцов, используемых для дрейфа).
Случайным распределением уровней факторов z элементом указанных столбцов матрицы без столбцов для дрейфа.
В случае, когда число опытов ограничено, кроме столбцов некоррелирующих с дрейфом для варьирования с остальными факторами можно использовать столбцы, входящие в разложение дрейфа с минимальными коэффициентами.
В этом случае влияние такого фактора будет влиянием дрейфа временного, но это искажение можно скорректировать по соответствующей формуле:
Билет 5