1.Оптимизация многофакторных объектов методом крутого восхождения
Рассмотрим процедуру оптимизации методом крутого восхождения на примере оптимизации двухфакторного процесса с целью отыскания режима (х1 и х2) при котором выходной показатель достигает максимального значения.
На первом этапе был реализован план 22=4 – опыта и условия опытов.
Полученные результаты представлены в виде таблицы.
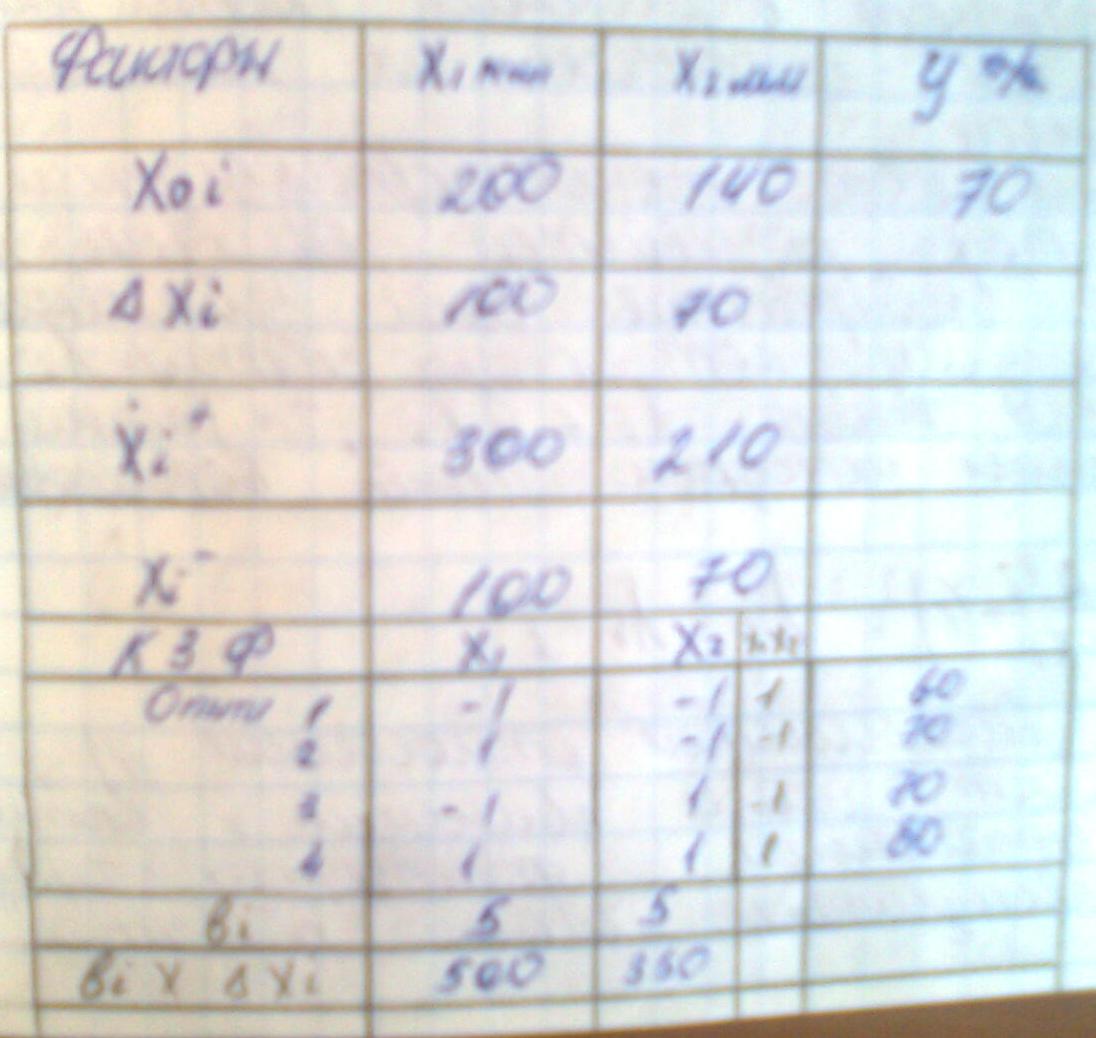
На следующем этапе значение коэффициента bi записывают в нижней части табл. и далее умножаем их на шаг варьирования.
Фактор
для которого такое произведение
– максимально, называется базовым и
для него выбирается шаг движения к
оптимизации, который обозначается
Он
выбирается обычно
,
те равный или меньше исходного шага
варьирования.
Далее вычисляется отношение (1) и определяют шаги движения и оптимума по остальным факторам через базовый. Полученные шаги обычно округляют.
Пользуясь
полученной моделью
,вычислим
значения выходного показателя в каждом
рассчитанном опыте крутого восхождения.
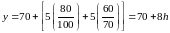
h – номер шага по крутому восхождению.
При достижении области оптимума, все коэффициенты линейной модели начинают убывать и проявляется действие эффектов факторов высшего порядка (эффектов взаимного влияния факторов и квадратичных эффектов фактора) поэтому для адекватного описания интересующей зависимости в области оптимальных режимов используют модели второго порядка (квадратичные модели).
2.Принципы планирования эксперимента в задачах оценки констант теоретических моделей и построения их аппроксимаций.
В этом случае объект представляется не черным, а серым ящиком, т.е.
структура зависимости выходного показателя y от исследуемых факторов x известна и представлена аналитической моделью типа систем алгебраических, дифференциальных, интегральных и смешанных моделей. Задача планирования эксперимента при этом сводится к оценке констант (параметров) таких моделей с максимальной точностью или не к построению полиномиальной аппроксимации такой аналитической модели. Такая аппроксимация может быть более удобна для оптимального управления исследуемым объектом и прогнозирования его поведения.
Существенной особенностью аналитических моделей является их нелинейность. Раннее рассмотренные модели были линейные по оцениваемым параметрам (и могли быть нелинейными только по факторам х).
Простейшим примером нелинейной алгебраической модели являются модели Моно (в биотехнологии) или Михаэлиса – Мента (в ферментальной кинетике).
В отличии от такого традиционного подхода по теории эксперимента для оценки двух параметров такой модели с максимальной точностью, достаточно сделать только 2 опыта, один из которых соответствует значению фактора x1= xmax (насыщение) в начальной зоне исследуемых режимах в зависимости от характера ошибки воспроизводимости выходного показателя у в исследуемом диапазоне режимов.
Поэтому наилучшим планом из двух опытов для оценки констант такой модели будут x1= xmax и
,
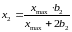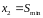при
,
при
,
при
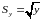
Для нахождения точек оптимального плана надо иметь хотя бы грубые значения искомых параметров модели (в данном случае b2).
Их можно получить из архивных данных или провести пробный эксперимент для примерочного оценивания таких параметров.
Используя такую двухэтапную процедуру – вычисляя значения факторов x в таком плане и через них уже новые значения параметров (в данном случае b2) можно проводить вычисления пока не стабилизируется значение обобщенного показателя качества оптимального плана эксперимента. Таким обобщенным показателем является детерминант (определитель) ковариационной матрицы (матрицы дисперсии ковариаций коэф. модели) или же детерминант информационной матрицы плана.
Критерий Д – оптимальности соответствует такому плану эксперимента при котором эллипсоид рассеяния значений параметров имеет минимальный объем.
Этот критерий обеспечивает совместное наиболее эффективное оценивание параметров искомой статистической модели.
Обычно на практике используют так называемые локальные – деоптимальные планы при которых в начале получают приближенные оценки параметров модели. На втором этапе определяют координаты – значения факторов х оптимального плана.
Билет 16