2.Методы построения обобщенных показателей (откликов) и многокритериальной оптимизации.

Реальные объекты характеризуются обычно не одним а комплексом выходных показателей, их качества или эффективности работы.

В таких системах желательно попытаться построить обобщенно-интегрированный показатель для которого далее построить модель его зависимости от исследуемых факторов или провести оптимизацию объектов. Существует несколько основных способов построения такого интегр. Показателя по значениям индивидуальных показателей.

1. Построение обобщенного показателя аддитивного типа, т.е. в виде суммы значений индивидуального показателя или суммы их значений с коэффициентами весомости.

Y=сумма(yi) либо Y=сумма(ai*yi)

2. Обобщенный показатель мультипликативного типа. Он в виде произведения индивидуальных показателей с коэффициентами, задаваемыми экспертным способом.

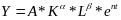
Пример: производственная функция Кобба-Дугласа – основной макроэкономический показатель для сравнения эффективности отдельных производств и национальных экономик.

Y характеризует кол-во продукции, кот производит отдельная фирма отрасль или макроэкономика

К – объем капиталовложений

L – объем трудовых ресурсов

N – интенсивность использований

3. Построение функции желательности Харрингтона

Предполагает переход от значений индивидуальных показателей y, измеряемым в своих физических величинах, к их значениям на психофизиологической шкале желательности.

На оси ординат нанесены значения желательности, изменяющиеся от 0 до 1. По оси абсцисс указаны значения отклика, записанные в условном масштабе.

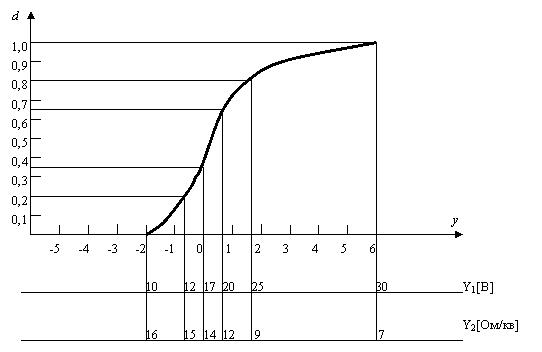
Используется несколько дискретных значений и интервалов желательности di.

Очень хорошо Хорошо Удовлетворительно Плохо Очень плохо

1,00 – 0,80 0,80 – 0,63 0,63 – 0,37 0,37 – 0,20 0,20 – 0,00

После определения значений желательности для исследуемых образцов по каждому исследуют показатель – значение обобщенной желательности.

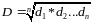
4. Использование функции потерь качества.

L=k(y-y_n)²

y_{n –} наилучшее номинальное значение индивидуального показателя, измеренное в своих физ. Единицах

y – значение для конкретной единицы продукции

L – потери в денежных единицах

К – коэффициент пропорциональности, связывающий изменчивость контролируемого индивидуального показателя y относительно желательного номинала.

L характеризует новые концептуальные понятия качества продукции. Согласно этому понятию качество продукции оценивается величиной потерь, которые несет все обество после того как продукция поступила в эксплуатацию.

Достоинства:

1. для его расчета на производстве любой продукции уже есть все необходимые данные

2. он очень удобен для многокритериальной оценки качества, поскольку при этом значения каждого индивидуального показателя пересчитывают в денежные потери. Их можно складывать и сравнивать.

Этот показатель продемонстрировал несовершенство мировой практики сравнения производств однотипной продукции только по величине допуска на выходные показатели y. Согласно же L при одинаковом допуске эффективность сравниваемых производств может отличаться в разы.

Билет 15