1. Валки. 2,3. Перегородки.

Основным рабочим органом этих абсорберов является горизонтальный вал на котором закреплены лопасти или диски, слегка погруженные в жидкость. При вращении они захватывают жидкость и разбрызгивают её- Валки устанавливают в камерах так, что газ движется перпендикулярно или параллельно осям валков. При этом, по ходу движения газа размещают перегородки.

П ри небольшом числе оборотов валков факел распыла симметричен оси валка, но радиус факела мал (300 - 500 мм), а капли крупные. С увеличением чис­ла оборотов размер капель уменьшается, а размеры факела увеличиваются, при­чём, он начинает отклоняться от вертикальной оси в сторону противоположную вращению валков (до 700 об/мин).

Рис. 130. Схема абсорбера с разбрызгивающими дисками.

1. Вал; 2. Диски; 3, Перегородив.

3.3.3.3. Центробежные абсорберы Схема аппарата центробежного типа приведена на рис.131

На валу 1 укреплён ротор 2 с кольцами 3, между которыми расположены неподвижные кольца статора 4. При вращении ротора жидкость поднимается по внутренней поверхности колец 3 и под действием центробежной силы разбрызги­вается с их верхних обрезов. Распылённая жидкость ударяется о неподвижные кольца 4 и стекает в ротор, после чего распыляется на следующем (считая от цен­тра) кольце 3. Газ движется в зазорах между вращающимися и неподвижными кольцами (противотоком или прямотоком) пересекая факел распыла жидкости.

Рис. 131. Схема центробежного абсорбера.

1. Вал. 2. Ротор; 3. Кольца ротора; 4. Кольца статора,

Разновидностью такого абсорбера является аппарат Алешина в котором неподвижные кольца 4 заменены на радиальные лопатки.

Испытаны центробежные абсорберы в которых статор прикреплён к рото­ру и вращается вместе с ним, или статор вращается в направлении противополож­ном ротору. Последний случай оптимален.

Поскольку центробежная сила в этих аппаратах во много раз превышает силу тяжести имеются аппараты и с горизонтальным расположением вала.

4. Сравнение абсорбционных аппаратов различных типов.

Эффективность работы аппаратов оценивается по следующим характеристикам:

1. Равновесное (парциальное) давление поглощаемого компонента в га­зовой фазе над уходящей жидкостью.

Если указанное давление равно нулю или мало, то можно применять с одинаковым успехом как противоток, так и прямоток (Прямоток дает меньшее гидравлическое сопротивление). Если равновесное давление компонента над ухо­дящей жидкостью велико и превышает требуемое парциальное давление компо­нента в уходящем газе, то необходим противоток.

2. Необходимое число единиц переноса.

Единица переноса или теоретическая тарелка это элемент абсорбера, ограниченный двумя поперечными сечениями, с такой высотой, что в нем изме­нение концентрации поглощаемого компонента в любой из фаз равно средней движущей силе абсорбции в этом элементе. Причем, под средней движущей си­лой абсорбции понимают среднюю (в данном элементе) разницу концентраций поглощаемого компонента в одной из фаз и равновесную его концентрацию в той же фазе при тех же условиях абсорбции.

Число теоретических тарелок определяется конструктивными размера­ми и типом абсорбера при неизменных условиях абсорбции и типах абсорбата и абсорбента, т.е. некий конкретный абсорбер с конкретными размерами и устрой­ством при определённых давлении и температуре по отношению к поглощению одного компонента имеет n₁ теоретических тарелок, а по отношению другого компонента n₂ теоретических тарелок.

Чем совершеннее конструкция аппарата по приспособленности к по­глощению данного компонента, тем большее число теоретических тарелок поме­щается в единице его высоты.

Если равновесное давление компонента над уходящей жидкостью равно нулю, число теоретических тарелок в аппарате не зависит от вида взаимного дви­жения фаз. Если же равновесное давление над уходящей жидкостью не равно ну­лю, то при противотоке в аппарате будет больше теоретических тарелок.

Если для поглощения данного компонента необходимо много теорети­ческих тарелок, то это требует аппаратов большой высоты или нескольких после­довательно соединенных аппаратов, или аппаратов такой конструкции, чтобы вы­сота теоретической тарелки была минимальна.

Существуют специальные расчеты для определения необходимого чис­ла теоретических тарелок для заданного поглощения данного компонента кон­кретной жидкостью.

3. Отношение объемных расходов жидкости и газа.

Это отношение определяется на основе материального баланса содер­жанием компонента в поступающем и уходящем газе, а также в поступающей и . уходящей жидкости. В обычных условиях это отношение изменяется в пределах от 0,0005 до 0,005. Чем совершеннее абсорбер, тем меньше это соотношение при прочих равных условиях.

4. Отвод выделяемого тепла.

Отвод тепла, выделяющегося при абсорбции, может производиться ли­бо охлаждением в выносных холодильниках, либо путём внутреннего охлажде­ния, либо охлаждением за счёт испарения части поглотителя. Первый способ наи­более распространен, но он наихудший, ибо требует перекачки жидкости при низком коэффициенте теплопередачи. Последний способ не всегда возможен. По­этому, тот абсорбер лучше, что позволяет применить внутреннее охлаждение.

5. Давление.

Повышение давления благоприятно влияет на процесс абсорбции, т.к. ведёт к повышению коэффициента массопередачи и движущей силе абсорбции. Кроме того, при повышенных давлениях объём газа снижается, что позволяет уменьшить диаметр аппарата.

Абсорбция под давлением проводится в тех случаях, когда давление всё равно необходимо по ходу технологического процесса. Специальное сжатие газов для проведения абсорбции практически не применяют.

Чем больше давление, под которым может работать аппарат, тем совер­шеннее его конструкция.

6. Гидравлическое, сопротивление.

При проведении абсорбции под повышенным давлением гидравличе­ское сопротивление абсорбера несущественно. Если же абсорбцию ведут при дав­лениях близких к атмосферному, то желательно чтобы аппарат имел как можно шоке гидравлическое сопротивление. Сравнение лучше всего проводить по поте­ри давления на одну теоретическую тарелку при оптимальном режиме. Чем она меньше, тем лучше аппарат. Обычно, эти потери находятся в диапазоне 20 - 500 Па/1 т.т.

7. Интенсивность.

Под ней понимают отношение объёма аппарата к объёму подаваемого в одну секунду газа. Чем меньше эта величина, тем лучше аппарат.

Барботажные абсорберы, как правило, интенсивнее насадочных. Ещё более интенсивны плёночные абсорберы с восходящим прямотоком и скоростные прямоточные распиливающие абсорберы.

При абсорбции плохо растворимых газов интенсивность (обычно со­ставляющая 1-20 с'¹) заметно снижается.

8. Пределы изменения нагрузок по жидкости и газу.

На практике данные нагрузки часто колеблются в широких пределах. Это ведёт к изменению режима работы абсорбера, его эффективности и гидравлического сопротивления; в результате, требуемая степень очистки газа может не достигаться.

Чем в более широком диапазоне изменения данных нагрузок может ра­ботать абсорбер, тем он совершеннее.

9. Время пребывания жидкости и газа в абсорбере.

Время пребывания жидкости и газа в абсорбере определяется их коли­чеством, находящимся в аппарате. Время пребывания газа всегда меньше жидко­сти. Длительное время пребывания для газа необходимо если абсорбция идёт медленно. Малое время необходимо, как правило, для селективной очистки. Дли­тельное время пребывания для газа и жидкости необходимо для максимального приближения к равновесию.

Оптимальный абсорбер тот, что позволяет варьировать этими параметра­ми.

10. Наличие в газе или жидкости загрязнений.

При наличии загрязнений, а также в случае выпадения осадков в про­цессе абсорбции возможно забивание абсорбера и нарушение его работы. Чем лучше абсорбер, тем меньше он чувствителен к загрязнениям.

11. Масштаб производства.

Чем в большем диапазоне нагрузок по газу может работать абсорбер, . тем совершеннее его конструкция.

12. Коррозионное воздействие среды.

Чем более устойчив абсорбер к коррозионной активности среды, тем он совершеннее.

Основные сравнительные характеристики наиболее распространённых аб­сорбционных аппаратов приведены в табл. 35.

Табл.35.

Основные сравнительные характеристики наиболее распространённых абсорбционных аппаратов

Показатели

Пленочные абсорбер

Насадоч. аб.

Барботажные абсорберы

Распылительн. Абс.

Трубчатые

Листовые

Восх прямоточн

Внавал

Регулярные

Затоп. насад.

Колпачковые

Ситчатые

Провальные

Пластинчатые

Пла.насад.

Мех. пер.

Форсуночные

Скорост.

Механ.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

Возможность осуществления противотока в одной ступени. Возможность достижения в одном аппарате числа т.т.: <2 2 – 5 5 – 10 >10 Возможность работы с отношением Vж/Vг: < 0,001 0,001 – 0,005 >0,02 Осуществимость внутреннего отвода тепла Низкое гидравлическое сопротив. Возможн.широкого измен.нагрузок по газу и жидкости Длител.пребыван. жидкости Работа при загряз. Расход газа (м3/ч): <1000 1000 – 10000 10000 – 100000 Простота конструк. Работа в агрессивных средах

+ + + - - - + - + + + - х + + х х х

+ + + + + - + - - + + - х + + + х х

- + х х - + - - + - х - - + + + - х

+ + + + х - х + - х + + - + + + + +

+ + + + х - + + - + + х х х + + + +

+ + + + + + + х - - х + - + х - х +

- + + + + + + - + - + + + х + + - х

- + + + + + + х + - х х + + + + х х

- + + + + + + х + - - - + + + + + х

- + + + + + + + - + + + + + + + + х

- + х - - - + - - - х - + х + + + +

- + - - - - - + + - + + + + - - - х

Х + х - - - - + - + х - х х + + + +

- + х - - - + - - - - - х + + + + +

- + х - - + + + - + + + + + + х - х

Условные обозначения:

+ соответствие требованию; х – частичное соответствие; - несоответствие

Практическое занятие № 36

5. Технологический расчет абсорберов

5.1. Способы выражения концентраций компонентов

Составы газовой и жидкой фаз могут быть выражены в мольных или массовых соотношениях. Наиболее распространены следующие способы выражения состава:

1. Состав выражают в виде объёмной концентрации, т.е. числа киломолей или килограммов компонента, содержащихся, содержащихся в единице объёма фазы. Единица измерения объёмной концентрации с (или ) равна кмоль/м³ (или кг/м³).

2. Состав выражают в мольных (или массовых) долях компонента по отношению к общему количеству вещества в данной фазе. Состав, выраженный в мольных (или массовых) долях, будем обозначать для газовой фазы через (или ); для жидкой – через х (или ).

3. В системах с носителем состав можно выразить в виде относительной концентрации, т.е. в виде отношения числа киломолей (или килограммов) компонента к числу киломолей (или килограммов) носителя. Мольную (или массовую) относительную концентрацию будем обозначать для газовой фазы через (или ), для жидкой – через (или ).

Состав газовой фазы часто выражают через парциальные давления.

Если Р – общее давление газовой смеси и у – мольная доля компонента, то парциальное давление компонента:

(632)

Парциальное давление инертного газа (при содержании в смеси лишь одного компонента):

(633)

Данные формулы справедливы только для газов, подчиняющихся законам идеальных газов. В этом случае, мольная доля численно равна объёмной доле; связь между мольной долей компонента у и его объёмной концентрацией с выражается уравнением:

(634)

где: Р – общее давление в кПа.

В табл. 36 и 37 приведены соотношения между различными способами выражения составов газовой и жидкой фаз. В этих соотношениях - мольная масса компонента; и - средние мольные массы газовой и жидкой фаз; и - мольные массы носителя в газовой и жидкой фазах; - плотность жидкой фазы, кг/м³.

Входящая в приведённые соотношения средняя мольная масса определяется по следующим уравнениям::

(635)

(636)

Соотношения, приведённые в табл. 36 и 37, применимы как к бинарным, так и к многокомпонентным системам, причём, под знаком суммы стоят величины для всех компонентов кроме носителя. Для бинарных систем в членах ( , и т.д.) содержащих знак суммирования, этот знак опускается.

Относительные концентрации выражаются числами большими, чем мольная (или массовая) доля. При небольшом содержании компонента (при y < 0,03 и х < 0,03) можно с достаточной точностью считать эти величины равными (y~Y, ).

Наиболее удобно выражать состав газовой фазы через мольные доли (у) или парциальные давления (р), т.к. эти способы выражения состава не зависят от температуры газа. Состав жидкой фазы наиболее удобно выражать в мольных долях (х) или объёмных концентрациях (с).

В зависимости от принятых единиц концентрации константа фазового равновесия (m) выражается различными величинами. Для обозначения единиц концентрации будем писать эту константу с двумя индексами, из которых первый относится к единицам концентрации газовой фазы, а второй – к единицам концентрации жидкой фазы. Если концентрации обеих фаз выражены в величинах с (кмоль/м³) или (кг/м³), будем ограничиваться одним индексом.

Т аким образом:

(637); (638); (639); (640) и т.д.

Причём, верхний индекс – звёздочка относится к концентрации газа, равновесной с соответствующей концентрацией жидкости.

Если концентрация газа и жидкости выражены в одинаковых единицах измерения, то константы фазового равновесия безразмерны. Если же для концентраций газа и жидкости приняты единицы различной размерности, то константа фазового равновесия размерна.

Соотношения между различными формами констант фазового равновесия приведены в табл.38.

Константа численно равна константе и поэтому в таблице не приведена.

Наиболее удобны константы фазового равновесия и .

Практическое занятие № 37

5.2. Расчет противоточной изотермической абсорбции в насадочной аппарате.

1. Составление материального баланса и определение расхода абсорбента

Рассчитаем расход (кмоль/час) поглощаемого компонента, поступающего в абсорбер:

(638)

где:

- расход газа на входе в абсорбер (кмоль/час);

- содержание поглощаемого компонента (доли ед.).

Определим расход (кмоль/час) поглощенного в абсорбере компонента:

(639)

где:

- требуемая степень извлечения компонента из исходного газа.

Найдём расход газа (кмоль/час), уходящего из абсорбера:

(640)

Вычислим содержание (доли ед.) поглощаемого компонента в уходящем газе:

(641)

Константу фазового равновесия при растворении поглощаемого компонента в абсорбенте (в рабочих условиях) определим по эмпирическому уравнению Зельвенского:

(642)

где:

- парциальное давление поглощаемого компонента в поступающем газе (МПа);

и - постоянные, которые в зависимости от температуры имеют значения, представленные в табл. 39.

Табл.39.

Значения постоянных и

Температура, 0С	0	25	50	75	100
	1,84000	0,75500	0,42500	0,30800	0,23100
	0,26500	0,04280	0,01590	0,00985	0,00328

Промежуточные значения коэффициентов определяются методом экстраполяции.

Парциальное давление поглощаемого компонента в поступающем газе составит:

(642)

где: Р – общее давление в абсорбере (МПа).

В более общем случае значения константы фазового равновесия определяется по справочной литературе.

Равновесная концентрация поглощаемого компонента в жидкости определяется по уравнению:

(643)

Минимальный расход абсорбента при противотоке ( ) находим, полагая, что концентрация поглощаемого компонента в абсорбенте на выходе из абсорбера ( ) достигнет величины , т.е.: :

(644)

Поскольку ни в одной конструкции абсорбера равновесие не достигается, полученное минимальное количество абсорбента необходимо искусственно увеличить.

Для противоточных насадочных абсорберов это увеличение обычно колеблется на уровне 30 %.

Тогда, расход абсорбента, поступающего в абсорбер ( ), составит:

(645)

Расход жидкости, покидающей абсорбер ( ), определяется по уравнению:

(646)

Выполняя данный расчет из – за малой величины мы пренебрегли разницей в молекулярных массах поглощаемого компонента и абсорбента.

Тогда истинное содержание (доли ед.)поглощаемого компонента в уходящем абсорбенте ( )составит:

(647)

2. Вычисление данных для построения рабочей линии.

Рабочей линией называется зависимость между концентрацией поглощаемого компонента в газовой и жидкой фазе в произвольном сечении аппарата.

Определим удельный расход поглотителя на входе в абсорбер:

(648)

Уравнение рабочей линии имеет вид:

(649)

где: х и у – текущие значения соответствующих концентраций.

Ограничимся определением х в точке, соответствующей среднему значению концентрации компонента в газовой фазе ( ):

(650)

Тогда, соответствующее значение концентрации компонента в жидкой фазе ( ) можно найти из уравнения:

(651)

3. Вычисление данных для построения линии равновесия.

Линией равновесия называется зависимость между равновесными концентрациями поглощаемого компонента в газовой и жидкой фазе в произвольном сечении аппарата.

Равновесная концентрация поглощаемого компонента на входе в абсорбер ( ) находится по уравнению:

(652)

где:

константу фазового равновесия на входе в абсорбер ( ) находят по уравнению (642) с учетом данных табл.39.

Равновесная концентрация поглощаемого компонента на выходе из абсорбера ( ) находится по уравнению:

(653)

где:

константу фазового равновесия на выходе из абсорбера ( ) находят по уравнению (642) с учетом данных табл.39., предварительно рассчитав парциальное давление поглощаемого компонента на выходе из абсорбера (р₂) по формуле:

(654)

Равновесная концентрация поглощаемого компонента в средней точке абсорбера :

(655)

где:

константу фазового равновесия на выходе из абсорбера ( ) находят по уравнению (642) с учетом данных табл.39., предварительно рассчитав парциальное давление поглощаемого компонента на выходе из абсорбера ( ) по формуле:

(656)

4. Определение числа теоретических тарелок.

Рассчитаем величину движущих сил:

На входе газа в абсорбер:

(657)

В средней точке:

(658)

На выходе газа из абсорбера:

(659)

Определим следующее соотношение:

(660)

Если соотношение (660) окажется меньше 6, то число теоретических тарелок можно рассчитать по следующему уравнению:

(661)

Если соотношение (660) окажется , то диапазон необходимо разделить не на 2 участка (как в рассматриваемой методике), а на большее число частей. В каждой определить граничные и средние значения движущей силы и по ним рассчитать необходимое число теоретических тарелок для каждой части. А затем. Полученные результаты просуммировать.

5. Определение диаметра абсорбера.

Найдём массовые расходы газа и жидкости:

Расход газа на входе в абсорбер ( ):

(662)

где:

молекулярная масса газа ( ) может быть вычислена по формуле:

(663)

где:

- молекулярная масса - го компонента газа;

- объёмная (мольная) доля - го компонента газа.

Расход жидкости на входе в абсорбер ( ):

(664)

где:

- молекулярная масса жидкости.

Если скорость газа будет мала, то в аппарате будет наблюдаться режим захлёбывания, т.е. весь свободный объём аппарата будет заполнен жидкостью и газ не сможет в него поступать.

Если скорость газа будет высока, то в аппарате будет наблюдаться режим подвисания, т.е. весь свободный объём будет заполнен газом и жидкость не сможет в него поступать.

Осуществим расчет исходя из определения скорости захлёбывания ( ):

Известно, что концентрация поглощаемого компонента в газовой фазе в произвольном сечении аппарата (у) может быть вычислена по следующей зависимости:

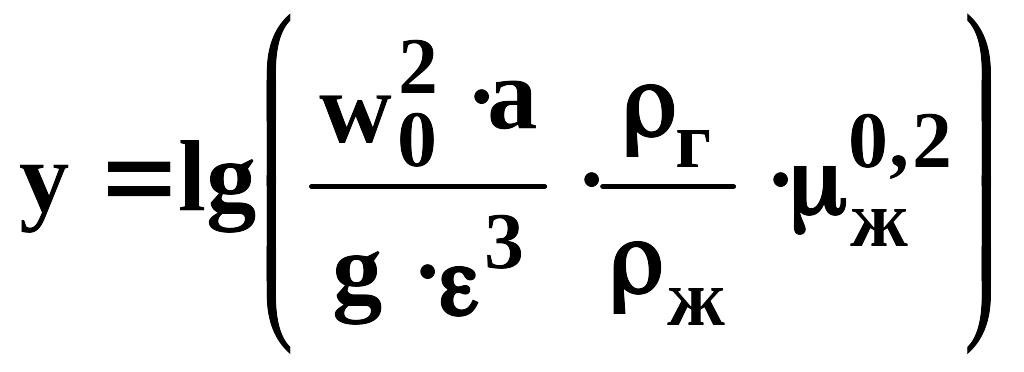(665)

где:

а – удельная поверхность насадки;

- свободный объём орошаемой насадки.

Значения величин а и берутся из справочной таблицы 40.

Определим плотность газа, приходящего в абсорбер, в условиях аппарата, для чего воспользуемся соотношением:

(666)

где:

- объёмный расход газа в условиях абсорбера (м³/час).

Данную величину рассчитаем по соотношению:

(667)

где:

- давление при н.у. (1 атм.);

- объёмный расход газа при н.у.;

- температура в абсорбере;

- температура при н.у. (273 К);

- давление в абсорбере.

Табл.40.

Характеристики некоторых насадочных материалов

Вид насадки	Размеры элемента, мм	Число элементов в 1 м3 объёма насадки	Свободный объём ( ) м3/м3	Удельная поверхность (а), м2/м3	Масса 1 м3 насадки, кг
Кольца: Фарфоровые Керамические Керамические Керамические Керамические Стальные Стальные Гравий кругл. Андезит куск. Кокс кусков. Кокс кусков. Кокс кусков. Кокс кусков.	8х8х1,5 15х15х2 25х25х3 35х35х4 50х50х5 35х35х2,5 50х50х1 42 43,2 42,6 40,8 28,6 24,4	1465000 250000 53200 20200 6000 19000 6000 14400 12600 14000 15250 27700 64800	0,64 0,70 0,74 0,78 0,785 0,83 0,95 0,388 0,565 0,56 0,545 0,535 0,532	570 330 204 140 87,5 147 110 80,5 68 77 86 110 120	600 690 532 505 530 - 430 - 1200 455 585 660 600

Плотность и вязкость жидкого поглотителя, приходящего в абсорбер, берут из справочной литературы.

С другой стороны, известно, что концентрация поглощаемого компонента в газовой фазе в произвольном сечении аппарата (у) может быть вычислена по следующей зависимости:

(668)

где:

концентрация поглощаемого компонента в жидкой фазе в произвольном сечении аппарата (х) может быть вычислена по уравнению:

(669)

Таким образом, определив (х) по уравнению (669) и найдя с его помощью (у) по уравнению (668) мы получаем возможность подставит полученный результат в уравнение (665) и, наконец, найти искомую величину ( ).

Чтобы абсорбер мог работать в реальных условиях, принимаем рабочую скорость газа ( ) равную:

(670)

Отсюда, необходимая площадь сечения абсорбера:

(671)

Но:

Откуда не составляет труда найти внутренний диаметр аппарата, который для создания некоторого запаса надёжности необходимо увеличить примерно на 10 %.

После этого необходимо реальную площадь сечения абсорбера ( ) и соответствующие ей массовые скорости газа и жидкости:

(672)

(673)

6. Определение высоты одной теоретической тарелки для газовой фазы.

Определим эквивалентный диаметр насадки:

(674)

Вычислим критерий Рейнольдса и Прандтля для газа:

(675)

(676)

где:

- коэффициент диффузии поглощаемого компонента в остальном газе:

(677)

где:

Р – давление абсолютное, атм.;

Т – температура, К;

М_А и М_В – мольные массы поглощаемого компонента и всего остального газа;

v_A и v_B - мольные объёмы (см³/атом) поглощаемого компонента и остального газа, определяемые как сумма атомных объёмов, входящих в состав газа, определяемых по табл.41.

Табл.41.

Атомные и мольные объёмы элементов

Атомный объём, м3/атом

Мольный объём, м3/атом

Воздух 0,0000270 С 0,0000148 Cl 0,0000246 Н 0,0000037 Nв первичных аминах 0,0000105 Nво вторичных аминах 0,0000120 Nс двумя насыщенными связями 0,0000156 Ос двумя насыщенными связями 0,0000074 Ов альдегидах и кетонах 0,0000074 Ов сложных эфирах 0,0000091 Ов простых эфирах 0,0000099 Ов высших простых и сложных эфирах 0,0000110 Ов кислотах 0,0000120 Ов соединениях с S, P, N 0,0000083 S 0,0000256 I 0,0000370

H2 0,0000143 O2 0,0000256 N2 0,0000312 Воздух 0,0000299 CO 0,0000307 CO2 0,0000340 SO2 0,0000448 NO 0,0000236 N2O 0,0000364 NH3 0,0000258 H2O 0,0000189 H2S 0,0000329 COS 0,0000519 Cl2 0,0000484 Br2 0,0000532 I2 0,0000715

Структурные постоянные:

Бензольное кольцо 0,000015

Нафталиновое кольцо 0,000030

Антраценовое кольцо 0,0000475

При расчете мольного объёма химического соединения величину соответствующей структурной постоянной надо прибавлять к сумме атомных объёмов.

Искомая величина высоты теоретической тарелки по газу находится по соотношению:

(678)

7. Коэффициент диффузии поглощаемого компонента в жидкости можно рассчитать по формуле:

(679)

где:

значения коэффициента «А» для ряда веществ, растворенных в жидкости, выбираются из табл. 42.

Табл.42

Значения коэффициента «А»

Вещество	Коэффициент «А»
Газы Этиловый спирт Метиловый спирт Уксусная кислота	1 1,24 1,19 1,27

Значения коэффициента «В» для ряда веществ выбирается из табл.43.

Табл. 43

Значения коэффициента «В»

Вещество	Коэффициент «В»
Вода Этиловый спирт Метиловый спирт Уксусная кислота Неассоциированные жидкости	4,7 2,0 2,0 1,15 1,0

- мольный объём жидкости (см³/атом) определяется по данным табл. 41;

М_ж – молекулярная масса жидкости, определяется по данным периодической таблицы элементов;

- динамическая вязкость жидкости, определяется по справочной литературе.

Осуществляя подобные расчеты изменением вязкости жидкого поглотителя при растворении в нём поглощаемого компонента пренебрегаем.

Вычисли критерий Рейнольдса и Прандтля для жидкости:

(680)

(681)

Рассчитаем приведённую толщину плёнки жидкости:

(682)

Определим высоту одной теоретической тарелки по жидкости:

(683)

8. Определение высоты насадки.

Среднее количество молей поглощаемого компонента в абсорбере в газовой фазе:

(684)

Принимая число точек орошения насадки (n), находим так называемые коэффициенты ухудшения по уравнению:

(685)

(686)

где:

d – внутренний диаметр насадки, в см.

Коэффициент «С» выбирается исходя из данных табл. 44.

Табл. 44.

Значения коэффициента «С_г,ж»

Способ загрузки насадки	Сг	Сж
Упорядоченная укладка Загрузка внавал	88 15,7	40 2,7

Высота одной теоретической тарелки с учетом коэффициентов ухудшения может быть рассчитана по формуле:

(687)

Тогда, высота насадки:

(688)

где:

N – коэффициент запаса, обычно принимаемый равным 2.

Практическое занятие № 38

5.3. Расчёт неизотермической абсорбции с непрерывным отводом тепла (трубчатый аппарат).

1. Составление материального баланса и определение расхода поглотителя на абсорбцию.

Определим расход (кмоль/с) поглощаемого компонента на входе в абсорбер:

Зная молекулярную массу (М_А) поглощаемого компонента (согласно периодической таблице элементов Д. И. Менделеева) пересчитаем его расход на входе в абсорбер из кмоль/с в кг/с исходя из соотношения:

(689)

Найдем массовый расход поглощаемого компонента в абсорбере:

(690)

Определим массовый расход ( ) образующегося жидкого поглотителя после абсорбера:

(691)

где:

х₂ – концентрация (доли ед.) поглощаемого компонента в поглотителе после абсорбера.

Вычислим массовый расход абсорбента на входе в абсорбер:

(692)

Зная молекулярную массу (М_ж) жидкого поглотителя (согласно периодической таблице элементов Д.И.Менделеева) пересчитаем расход абсорбента на входе в абсорбер из кг/с в кмоль/с :

(693)

Тогда, удельный расход поглотителя:

(694)

Пересчитаем расход поглощаемого компонента из кг/с в кмоль/с, :

(695)

2. Определение расхода охлаждающего агента.

Интенсивность выделения тепла при поглощении аммиака составит:

(696)

где:

- Удельная теплота растворения поглощаемого компонента в абсорбенте.

Тогда массовый расход охлаждающего агента можно найти по уравнению:

(697)

где:

- теплоёмкость поглощающей жидкости в условиях абсорбции (берётся из справочной литературы).

3. Определение коэффициента теплопередачи к охлаждающей жидкости.

Определим так называемую линейную плотность орошения:

(698)

где:

- внутренний диаметр трубки;

- число трубок

(699)

где:

- толщина стенки трубки.

Перейдём к расчёту коэффициента теплоотдачи от поглощающей жидкости к стенке трубки ( ). Для этого придётся предварительно вычислить следующий ряд необходимых величин:

(700)

Определим так называемую приведённую скорость:

Найдём так называемое критическое значение числа Рейнольдса:

(701)

Если: < , то критерий Нусельта определим по формуле:

(702)

Таким образом:

(703)

Рассчитаем коэффициент теплопередачи К:

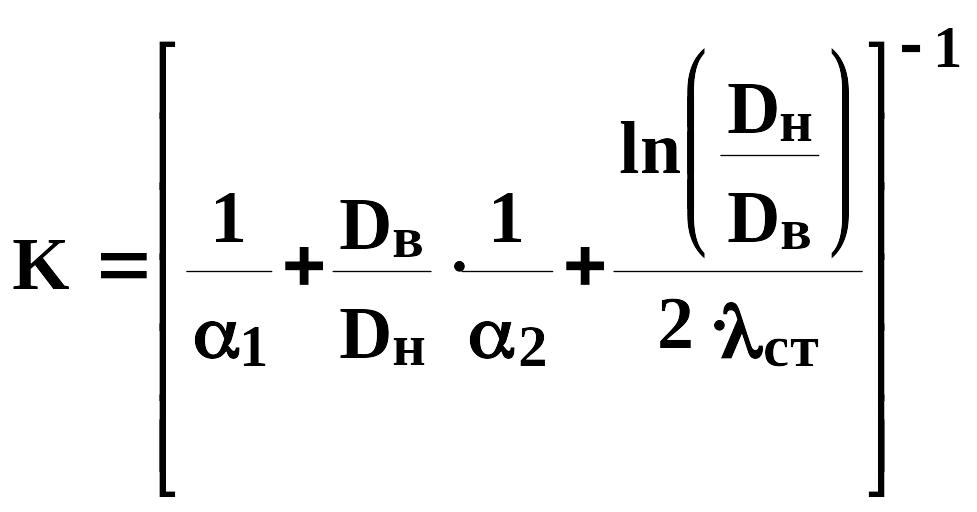(704)

Разумеется, что все значения коэффициентов теплоотдачи и коэффициента теплопередачи относятся к единице времени.

4. Определение коэффициента массоотдачи в газовой фазе.

Определим скорость газа в аппарате (на входе):

(705)

Затем, рассчитаем среднюю скорость жидкостной пленки в каждой трубке:

(706)

Далее определяем относительную скорость газа:

(707)

Найдём безразмерный комплекс (К):

(708)

где:

- поверхностное натяжение, выбираемое по справочной литературе, например, табл. 45.

Табл.45.

Примеры значений

Вещество	Поверхностное натяжение ( ), Н/м
	-200С	00С	200С	400С	600С	800С	1000С	1200С
Аммиак жидкий Аммиачная вода, 25 % Вода	0,0380 - -	0,0270 0,0657 0,0756	0,0212 0,0629 0,0728	0,0168 0,0597 0,0696	0,0128 0,0563 0,0662	- 0,0527 0,0626	- 0,0490 0,589	- 0,0450 0,0549

Вычисляем относительный критерий Рейнольдса:

(709)

Найдём средний критерий Прандтля:

(710)

где:

- коэффициент диффузии газа.

Определим парциальное давление инертных газов на входе в абсорбер:

(711)

Определим парциальное давление инертных газов на выходе из абсорбера:

(712)

Разумеется, при этом, гидравлическими потерями в абсорбере пренебрегаем.

Тогда, среднее парциальное давление инертных газов в абсорбере будет:

(713)

Коэффициент массоотдачи ( ) рассчитываем по уравнению:

(714)

Тогда, коэффициент массоотдачи в начале трубок:

(715)

Аналогично находим коэффициент массоотдачи ( ) на конце трубок (коэффициент изменяется вследствие уменьшения расхода и скорости газа, а так же повышения парциального давления инертных газов; изменением температуры газа пренебрегаем).

5. Определение коэффициента массоотдачи в жидкой фазе.

Предварительно рассчитаем средний критерий Прандтля для жидкости:

(716)

По формуле Борисова определим среднее значение критерия Нусельта для жидкости:

(717)

где:

l – длина трубок в абсорбере (принимается )

Откуда, коэффициент массоотдачи жидкости:

(718)

или:

(719)

где:

М_ж – молекулярная масса жидкости.

6. Определение коэффициента массопередачи.

На входе в абсорбер:

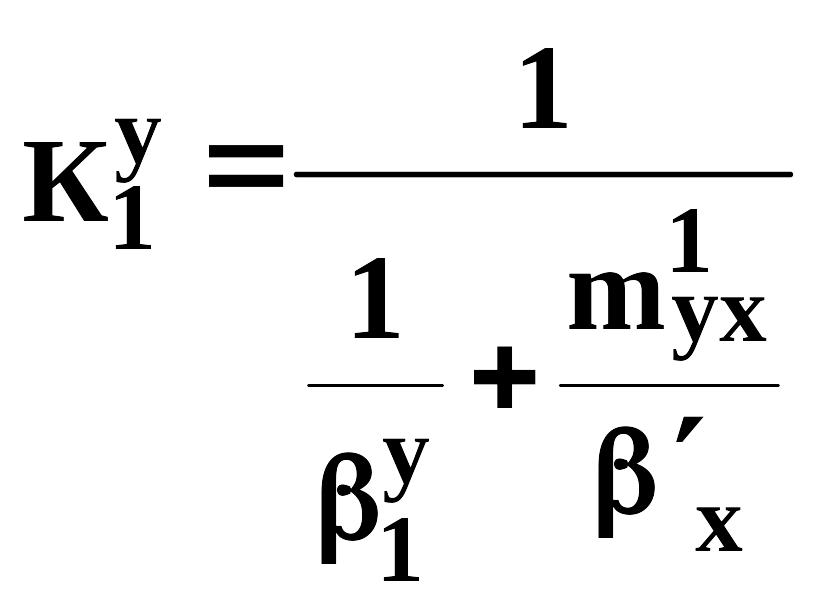(720)

где:

- константа фазового равновесия поглощаемого компонента на входе в абсорбер (определяется по справочной литературе).

На выходе из абсорбера:

(721)

где:

- константа фазового равновесия поглощаемого компонента на выходе из абсорбера (определяется по справочной литературе).

Для упрощения дальнейший расчет будем вести по среднему значению:

(722)

7. Определение среднего коэффициента теплоотдачи от газа к жидкости.

Для определения искомой величины воспользуемся уравнением:

(723)

где:

с_г – удельная теплоёмкость газа;

- среднее значение коэффициента массотдачи.

(724)

8. Расчет изменений концентраций и температур по длине труб.

Допустим, что охлаждающий агент подаём в межтрубное пространство снизу вверх так, что он движется прямотоком по отношению к газу и противотоком по отношению к поглощающей жидкости.

Таким образом, удельный расход тепла (количество тепла, передаваемого 1 кг хладоагента 1 кмоль поглощаемого вещества) составит:

(725)

Дальнейший расчет потребует решения ряда дифференциальных уравнений. Для этого предварительно определим ряд входящих в них коэффициентов.

а) т.к. поверхность охлаждения в данном случае равна поверхности соприкосновения фаз, то первый коэффициент :

(726)

б) второй коэффициент находится по уравнению:

(727)

где:

- мольная теплоёмкость газа.

в) третий коэффициент находится по уравнению:

(728)

г) четвёртый коэффициент находится по уравнению:

(729)

где:

- мольная теплоёмкость жидкости.

д) пятый коэффициент находится по уравнению:

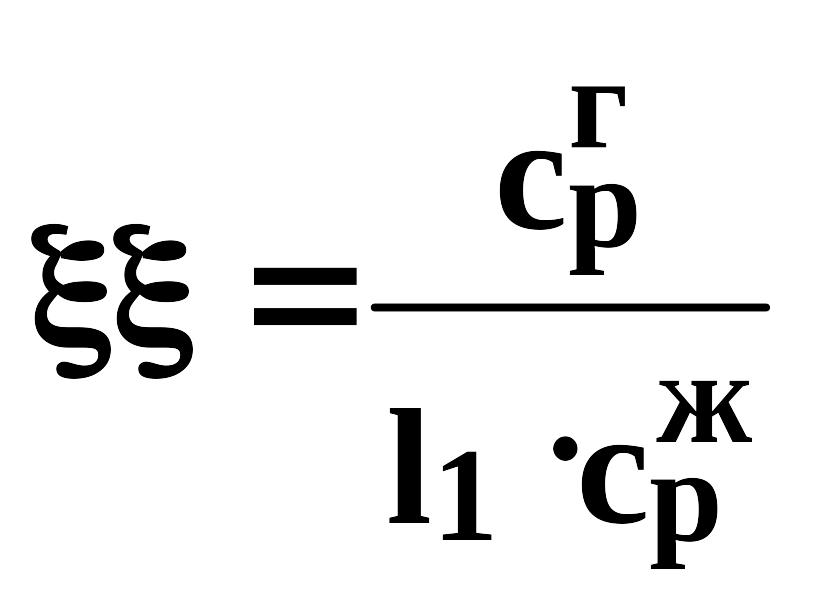(730)

е) шестой коэффициент находится по уравнению:

(731)

Перейдём к непосредственному решению дифференциальных уравнений. Расчет будем вести методом последовательных приближений, преобразовывая систему дифференциальных уравнений в интегральные. Интервал изменения z – степень поглощения извлекаемого компонента – разобьём на несколько участков. Нулевые приближения У принимаем в предположении линейного изменения У в зависимости от z; для и - равными граничным значениям: и .

Определим текущее значение температуры охлаждающего агента:

(732)

где:

- текущее значение температуры поглотителя.

(733)

- текущее значение концентрации поглощаемого компонента в газе.

- текущее значение температуры газа.

Определим текущее значение концентрации поглощаемого компонента в поглощающей жидкости:

(734)

где:

х₁ – концентрация поглощаемого компонента в поглотителе, приходящем в абсорбер.

Полученное значение текущей мольной концентрации поглощаемого вещества в жидком поглотителе необходимо пересчитать в текущую массовую концентрацию ( ), а для этого необходимо знать молекулярную массу газа (его состав). Рассмотрение этой операции опустим как элементарное.

Значения и можно определить проинтегрировав следующие выражения:

(735)

(736)

где:

N – число единиц переноса по газовой фазе, которое можно найти как:

(737)

где:

F – площадь поверхности труб.

Наконец, текущее значение температуры жидкости ( ) может быть определено по выражению:

(738)

где:

N₀ – искомое общее число единиц переноса.

Обозначим через I₁, I₂ и I₃ – соответствующие интегралы в пределах от 0 до z , а через , и в пределах от 0 до 1, причём:

(739)

(740)

Тогда:

(741)

Равновесные значения определяют по справочной литературе.

При решении уравнения (738) удаётся улучшить сходимость, проводя интерации с введением коэффициента . В данном случае этот коэффициент вводится при нахождении приближений t^г и t^ж , которые склонны к колебаниям. Таким образом, (р+1) приближения t^г и t^ж определяются по формулам:

(742)

(743)

При вычислении интегралов необходимо пользоваться формулой трапеций.

8. Определение поверхности контакта.

Рассчитаем движущую силу абсорбции:

(744)

Тогда, необходимая поверхность труб:

(745)

Откуда, длина труб:

(746)

Выбираем ближайшую стандартную длину труб. Отклонение от ранее принятой длины игнорируем. Принимаем соответствующий диаметр абсорбера.

Практическое занятие № 39

5.4. Расчёт абсорбции со ступенчатым отводом тепла (барботажный тарелчатый абсорбер).

1. Составление материального баланса и определение расхода жидкости на абсорбцию.

Определим расход инертного газа:

(747)

Содержание поглощаемого компонента в уходящем газе:

(747)

Определим концентрацию жидкости ( и ) в относительных мольных величинах (расчет предельно прост и аналогичен вышерассмотренному, а потому опущен).

Определим удельный расход поглотителя:

(748)

Тогда, расход поглотителя:

(749)

2. Определение диаметра абсорбера:

Количество газов на выходе из абсорбера составит (сам расчет в виду его предельной простоты и аналогичности расчета в выше рассмотренной задаче опускаем).

Тогда, среднее количество газов в абсорбере:

(750)

Зададимся средней температурой абсорбции ( ).

Пересчитаем среднее количество газа на эту температуру:

(751)

где:

N – объём, занимаемый 1 моль газа при н.у.

Принимаем внутренний диаметр абсорбера из имеющегося параметрического ряда ( ), чему соответствует сечение аппарата – S.

Тогда линейная скорость газа:

(752)

Если значение скорости получится в пределах, допустимых для данной конструкции внутренний диаметр подобран верно.

3. Выбор типа тарелки.

Принимаем решетчатые провальные тарелки с шириной прорезей (b) и живым сечением (w). На каждой тарелке располагаем охлаждающие элементы с поверхностью охлаждения на одну тарелку (F). Отношение поверхности охлаждения к площади тарелки:

(753)

Тогда, скорость газа в отверстиях:

(754)

4. Определение верхнего предела работы.

Средний массовый расход газа составляет:

(755)

где:

М_г – молекулярная масса газа.

Средний массовый расход жидкости составит ( ).

При плотности газа ( ) и плотности жидкости ( ) легко найти скорость газа в отверстиях. Фактическая скорость газа в отверстиях составляет 50 % от предельной.

5. Расчет сопротивления тарелки.

Сопротивление сухой тарелки (при ):

(756)

Средний объёмный расход жидкости:

(757)

Откуда, плотность орошения:

(758)

Сопротивление барботажного слоя (в Па) определяется по одному из эмпирических уравнений, полученных для конкретной системы на конкретных тарелках:

(759)

Полное сопротивление тарелки:

(760)

Определяем сопротивление, обусловленное поверхностным натяжением (при величине поверхностного натяжения и эквивалентном диаметре ).

(761)

Гидравлическое сопротивление слоя пены:

(762)

6. Определение высоты пены.

Находим высоту светлой жидкости:

(763)

Относительную плотность пены (k) рассчитываем по эмпирической формуле:

(764)

Высота пены на тарелке:

(765)

7. Расчет абсорбера по тарелкам.

Определяем коэффициент массопередачи:

(766)

Далее приводим расчет 1 –ой (нижней) тарелки, причём, для упрощения пренебрегаем различием между относительными составами газа и мольными долями.

а) Коэффициент массопередачи рассчитываем по эмпирической формуле:

(767)

б) Число единиц переноса на тарелку:

(768)

в) Эффективность тарелки (принимая полное перемешивание жидкости):

(769)

г) Относительный состав газа на выходе с тарелки:

(770)

где:

- равновесная концентрация поглощаемого компонента при температуре жидкости ( ) – определяется опытным путём.

д) Состав жидкости, поступающей на тарелку:

(771)

е) Принимая Е_т = Е_А, находим температуру газов на выходе с тарелки по формуле:

(772)

ж) Определяем максимальное количество тепла, которое может быть отведено охлаждающей жидкостью (коэффициент теплопередачи от барботажного слоя к охлаждающей жидкости принимаем равны k):

(773)

з) Задаваясь температурой жидкости при входе на тарелку ( ), из уравнения теплового баланса вычисляем количество тепла, отводимого с охлаждающей жидкостью:

(774)

и) Вычисляем:

(775)

и из соотношения:

(776)

находим Е₀.

к) Определяем температуру охлаждающей жидкости на выходе с тарелки:

(777)

л) Рассчитываем расход охлаждающей жидкости (при ей теплоёмкости ):

(778)

Аналогично производится расчет остальных тарелок до тех пор пока не будет достигнута заданная степень извлечения целевого компонента. Простым суммированием определяют общее сопротивление абсорбера и общий расход охлаждаюшей жидкости.

9. Определение расстояния между тарелками.

Принимая допустимый унос жидкости (u) находим минимальную высоту сепарационного пространства:

(779)

где:

поправочный множитель:

(780)

При высоте пены ( ) необходимое расстояние между тарелками:

(781)

6. Технологический расчет десорбера

6 .1. Расчет изотермической десорбции (схема процесса приведена на рис.132.)

Рис.132. Схема материальных потоков десорбера

1. Температура в десорбере.

Температура ввода сырья в десорбер (t₂) принимается из диапазона промышленных установок. Температура парогазовой смеси, выводимой из десорбера (t_п) принимается из диапазона промышленных установок. Температура жидкости, подаваемой для орошения верха аппарата (t₀) принимается из диапазона промышленных установок. Температура раствора после обмена теплом с более нагретой парогазовой смесью определяется из теплового баланса десорбера.

2. Материальный баланс десорбера.

Уравнение материального баланса десорбера имеет вид:

(782)

где:

Левая часть уравнения отвечает приходу материальных потоков.

- насыщенный раствор, подаваемый на регенерацию;

- отдувочный газ;

- жидкость, подаваемая на верх аппарата в качестве орошения;

- жидкость из испарителя.

Правая часть уравнения отвечает расходу материальных потоков.

- парогазовая смесь;

- жидкость в испаритель;

- регенерированный раствор;

- испарившееся орошение.

Для осуществления глубокой регенерации применяется отдувочный или отпарной газ, подаваемый под первую тарелку десорбера. Он уменьшает парциальное давление паров поглощенного компонента и тем самым способствует его переходу в паровую фазу.

Количество отдувочного газа рассчитывается по формуле:

(783)

где:

- количество абсорбента в насыщенном растворе;

- так называемый фактор десорбции;

К – константа равновесия в соответствующей системе.

Количество абсорбента в насыщенном растворе:

(784)

Фактор десорбции можно определить по диаграмме Кремсера (рис. 133); для этого предварительно принимается число теоретических тарелок (N_т) и рассчитывается степень отпарки парогазовой смеси в десорбере:

(785)

Р ис. 133. Расчетная диаграмма Кремсера

Т емпература отдувочного газа (конкретного состава) принимается равной t_г. Тогда константа фазового равновесия определяется по справочному графику; например, для системы ДЭГ – вода (рис.134)

Рис.134. Зависимость константы фазового равновесия в системе ДЭГ – вода от температуры и давления

Расход отдувочного газа составляет:

Расход отдувочного газа составляет:

(786)

или:

(787)

При этом, плотность газа:

(788)

Удельный расход отдувочного газа:

(789)

где:

- объёмное количество регенерируемого абсорбента.

Величина рассчитывается по формуле:

(790)

где:

- плотность регенерируемого абсорбента при температуре t₂, определяемая по справочной литературе.

Далее рассчитывают количество парогазовой смеси, выводимой из аппарата. Однократному испарению абсорбент подвергается дважды: первый раз – при вводе сырья G_гл.н. в десорбер и второй – при вводе нагретого в испарителе жидкого G_ж, полученного после однократного испарения сырья. При этом допускается, что при контакте с отдувочным газом состав насыщенного абсорбента после первого однократного испарения не меняется. Такое допущение обеспечивает резерв разделительной способности десорбера.

Мольная доля отгона рассчитывается путём подбора такого значения , при котором удовлетворяются равенства:

(791)

где:

и - содержание i-го компонента в жидкой и паровой фазах, образовавшихся при однократном испарении насыщенного абсорбента, мольн.доли.

К_i – константа фазового равновесия i-го компонента.

Однократное испарение насыщенного раствора G_гл.н. происходит при температуре t₂ и давлении Р. Однократное испарение жидкого потока G_ж – при температуре t₁ и давлении Р.

При этих условиях константы фазового равновесия находятся по справочной литературе.

Далее подбирают значения мольных долей отгона:

При первичном однократном испарении это - ;

При вторичном однократном испарении это - .

Массовые доли отгона равны:

При t_2, ⁰С:

(792)

При t_1, ⁰С:

(793)

После первого однократного испарения имеем:

Количество парогазовой смеси:

(794)

Количество жидкости:

(795)

После второго однократного испарения имеем:

Количество парогазовой смеси:

(796)

Количество жидкости:

(797)

Парогазовая смесь, образовавшаяся в результате однократных испарений, вместе с отдуыочным газом выводится из верхней части десорбера.

2. Тепловой баланс десорбера.

Уравнение теплового баланса в общем виде выглядит следующим образом:

(798)

Левая часть уравнения отвечает приходу тепла:

- с насыщенным раствором, подаваемым на регенерацию;

- с отдувочным газом;

- с нагретым в испарителе жидким остатком после однократного испарения потока ;

- с орошением верха десорбера.

Правая часть уравнения отвечает расходу тепла:

- с жидким остатком первого однократного испарения сырья, направляемым в испаритель;

- с парогазовой смесью и отдувочным газом;

- с регенерированным раствором;

- с испаряющимся орошением.

Количество тепла, вносимое в десорбер насыщенным раствором, рассчитывается по уравнению:

(799)

где:

- энтальпия парогазовой смеси, образовавшейся при однократном испарении сырья при температуре t₂;

- энтальпия жидкости ( ), образовавшейся при однократном испарении сырья при той же температуре.

Энтальпия парогазовой смеси ( ) рассчитывается по формуле:

(800)

где:

с_п – теплоёмкость парогазовой смеси.

Расчёт теплоёмкости парогазовой смеси производится в следующей последовательности. Предварительно определяется теплоёмкость пара раствора по формуле:

(801)

где:

Н – энтальпия пара при температуре t.

Энтальпия пара рассчитывается по формуле:

(802)

где:

h – энтальпия жидкости при температуре t₂;

r – теплота испарения при той же температуре.

Энтальпия жидкости:

(803)

где:

с – теплоёмкость жидкости при температуре t₂.

Теплота испарения жидкости при температуре t₂ определяется по справочной литературе.

Энтальпия раствора:

(804)

где:

с_ж – теплоёмкость раствора, содержащего х мас.дол. реагента при температуре t₂.

Количество тепла, которое вносится в десорбер отдувочным газом, рассчитывается по уравнению:

(805)

где:

с_р – теплоёмкость отдувочного газа при t = t₁.

Количество тепла, которое вносится в десорбер раствором при температуре t₁ рассчитывается по уравнению:

(806)

где:

- энтальпия парогазовой смеси, образовавшейся при однократном испарении потока G_ж при температуре t₁ .

- энтальпия жидкого потока , образовавшегося при однократном испарении потока .

Энтальпия парогазовой смеси, образовавшейся при однократном испарении раствора при температуре t₁ , рассчитывается по формуле:

(807)

где:

с_п – теплоёмкость парогазовой смеси, образовавшейся при втором однократном испарении раствора.

Расчёт теплоёмкости с_п при температуре t₁ подобен расчету теплоёмкости с_п при температуре t_{2 .}

Количество тепла, которое выносится из десорбера жидким остатком первого однократного испарения сырья при температуре t₂:

(808)

Количество тепла, которое выносит из десорбера парогазовая смесь при температуре t_п :

(809)

Количество тепла, которое выносит из десорбера регенерированный раствор при температуре t₁ :

(810)

Из теплового баланса десорбера имеем:

( + + ) + = ( + + ) + (811)

Величины, стоящие в круглых скобках, известны.

Обозначив их соответственно через и , можно записать:

- = - (812)

Решая последнее уравнение относительно количества оросительной воды, получим:

(813)

где:

- энтальпия водяного пара при температуре ;

- энтальпия воды при температуре .

4. Определение диаметра десорбера.

Диаметр десорбера в его наиболее нагруженном сечении (под нижней тарелкой) рассчитывают по формуле:

(814)

где:

- расход регенерированного раствора с нижней тарелки десорбера;

- плотность раствора при температуре ;

= 0,25 – коэффициент для тарелок с капсульными колпачками;

С = 550 – коэффициент для десорберов при расстоянии между тарелками = 0,6;

- расход парогазовой смеси, поступающей под нижнюю тарелку десорбера;

- плотность парогазовой смеси.

Плотность парогазовой смеси рассчитывается по формуле:

(815)

После определения диаметра десорбера выбирают ближайшее значение из нормального ряда диаметров колонн.

Ниже приведён принятый в нефтяной промышленности нормальный ряд диаметров колонн (в м), предусматривающий равномерное увеличение площади поперечного сечения колонны при переходе от одного диаметра к другому:

1,0; 1,2; 1,4; 1,6; 1,8; 2,0; 2,2; 2,4; 2,6; 2,8; 3,0; 3,2; 3,4; 3,6; 3,8; 4,0; 4,5; 5,5; 6,0; 6,4; 7,0; 8,0; 9,0.

5. Высота десорбера.

Рабочая высота десорбера:

(816)

где:

- высота верхней камеры колонны;

- высота верхней секции колонны, занятой тарелками;

- высота секции питания;

- высота нижней секции колонны, занятой тарелками;

- высота нижней камеры колонны.

Величины , , - принимаются из практических данных.

Высота верхней секции:

(817)

где:

- число рабочих тарелок в верхней секции аппарата.

Обычно число рабочих тарелок в верхней секции десорбера составляет 2 – 4.

Высота нижней секции:

(818)

где:

- число рабочих тарелок в нижней секции десорбера.

Известно, что число рабочих тарелок:

(819)

где:

- к.п.д. тарелок с круглыми колпачками, равный 0,1 – 0,3

Практическое занятие № 40

расчет отстойной аппаратуры

1. Общие сведения

   1. Классификация и основные свойства отстаивающихся систем.

Отстой – это разрушение (разделение) дисперсных систем под действием сил тяжести или центробежных сил.

Дисперсные системы – это механические смеси, состоящие, как минимум, из двух взаимно нерастворимых фаз, одна из которых распределена в другой.

Распределённая фаза – называется дисперсной средой или внутренней фазой.

Сплошная фаза – называется дисперсионной средой или внешней фазой.

Отстоем могут быть разделены системы дисперсная среда которых не участвует в броуновском движении и диффузии, а её плотность отличается от плотности дисперсионной среды.

Дисперсные системы бывают двухфазные и многофазные.

Двухфазные дисперсные системы подразделяются на:

а) суспензии (взвеси) – это жидкости со взвешенными твёрдыми частицами;

б) эмульсии – это жидкости со взвешенными в них капельками другой жидкости;

в) пены – это жидкости со взвешенными в них пузырьками газа;

г) пыли (дымы, аэрозоли) – это газы со взвешенными в них твёрдыми частицами;

д) туманы – это газы со взвешенными в них капельками жидкости.

1. Суспензии (взвеси).

В зависимости от размеров взвешенных частиц суспензии подразделяются следующим образом (табл.46.)

Таблица 46.

Классификация суспензий в зависимости от размеров взвешенных частиц

Наименование суспензии	Размеры взвешенных частиц, м.10-6
Грубая Тонкая Мути Коллоидные растворы	>100 0,5 – 100 0,1 – 0,5 < 0,1

Взвешенные частицы с размерами более 1^.10^-6 м уже не проходят через бумажные фильтры, видны в оптический микроскоп и практически не участвуют в броуновском движении и диффузии.

Различают седиментационную и агрегативную устойчивость суспензий.

Под седиментационной устойчивостью суспензий понимают их способность сопротивляться отстою.

Все суспензии с размерами взвешенных частиц более 1^.10^-6 м седиментационно неустойчивы.

Скорость отстоя (всплытия) зависит от размера частиц, их формы, разности плотностей внутренней и внешней фазы, а так же вязкости дисперсионной среды. На практике совокупное влияние этих параметров оценивают с помощью так называемой гидравлической крупности суспензии, под которой понимают скорость оседания (всплытия) частиц в мм/с в неподвижной жидкости. В качестве примера в табл.47 приведены значения гидравлической крупности частиц кварца в дистиллированной воде.

Таблица 47

Гидравлическая крупность кварцевых частиц в дистиллированной воде

Средний диаметр частиц, 1.10-6 м	20	2	0,2
Гидравлическая крупность, мм/с Время оседания частицы на 1 м, с	0,36 2600	0,0036 279000	0,000036 27900000

В случае полидисперсных систем пользуются среднеквадратичным радиусом частиц.

Под агрегативной устойчивостью суспензий понимают их способность сохранять свои первоначальные размеры частиц дисперсной фазы, т.е. не слипаться. Агрегативная устойчивость определяется плотностью поверхностного заряда частиц, их потенциала (потенциал Штерна), толщины двойного электрического слоя и интенсивности взаимодействия частиц со средой (лиофильности). Понижение этих параметров снижает агрегативную устойчивость суспензий. При отстое суспензий с малой агрегативной устойчивостью образуются более рыхлые осадки.

Различают суспензии свободнодисперсные и связнодисперсные. В первых частицы могут свободно перемещаться в среде; во – вторых частицы объединены в цепочки или сетки и либо вообще неподвижны, либо перемещаются единой массой. В этом случае, суспензии называются гелями. Гели представляют собой твёрдообразные «студенистые» тела, способные сохранять форму, обладающие упругостью и пластичностью. Для большинства гелей характерна тиксотропия. т.е. способность в изотермических условиях восстанавливать свою структуру после её механического разрушения. Гелеобразование возможно при содержании дисперсной фазы в суспензии в количестве всего нескольких % и даже долей %. Чем более анизометричны частицы и менее лиофильна их поверхность по отношению к дисперсионной среде, тем выше вероятность гелеобразования.

Гели, не обладающие тиксотропией, называются псевдогелями.

Большинство гелей термодинамически неустойчиво.

Разбавленные суспензии являются ньютоновскими жидкостями, их вязкость мало отличается от вязкости среды и линейно возрастает с ростом концентрации дисперсной фазы согласно закона Эйнштейна:

(820)

где: - вязкость суспензии;

- вязкость дисперсионной среды;

-содержание дисперсной фазы (сферические частицы).

Концентрированные суспензии, как правило, являются неньютоновскими жидкостями, вязкость которых стремительно нарастает даже при незначительном увеличении концентрации дисперсной фазы. Подобное явление объясняется процессом структурообразования.

Введём обозначения:

- масса суспензии;

- начальная концентрация дисперсной фазы в суспензии;

- конечная концентрация дисперсной фазы в суспензии;

- содержание жидкости в осадке;

- плотность частиц дисперсной фазы;

- плотность дисперсионной среды.

Тогда:

Масса осадка ( ):

(821)

Масса отстоявшейся жидкости ( ):

(822)

Плотность суспензии ( ):

(823)

Плотность осадка ( ):

(824)

2. Эмульсии.

Различают эмульсии прямые, обратные и множественные.

В прямых эмульсиях (эмульсии первого рода) в качестве дисперсионной среды выступает более полярная жидкость. Применительно к водо – нефтяным эмульсиям это эмульсии типа Н/В.

В обратных эмульсиях (эмульсии второго рода) в качестве дисперсионной среды выступает менее полярная жидкость. Применительно к водо – нефтяным эмульсиям это эмульсии типа В/Н.

В множественных эмульсиях капли дисперсной фазы содержат в своём объёме ещё более мелкие капли дисперсионной среды.

Эмульсии подразделяют на разбавленные, концентрированные и высококонцентрированные.

В первых на долю дисперсной фазы приходятся доли % от объёма эмульсии.

Во вторых на долю дисперсной фазы приходятся % и даже десятки % от объёма эмульсии.

В третьих (мази, кремы) на долю дисперсной фазы приходится более 90 % от объёма эмульсии.

Кроме основных типов эмульсий, названных выше, различают так называемые микроэмульсии и эмульсии Пиккеринга.

Первые представляют собой многокомпонентные системы, содержащие кроме двух жидкостей с ограниченной взаимной растворимостью, мицеллообразующие ПАВ. Размер частиц дисперсной фазы составляет (10 –100)^.10^-9м.

Вторые представляют собой один из трёх основных типов эмульсий, но с высоким содержанием твёрдых частиц, сконцентрированных на границе раздела фаз.

Все эмульсии характеризуются: дисперсностью, вязкостью, плотностью, электрическими свойствами и устойчивостью.

а) Дисперсность – это степень раздробленности дисперсной фазы в дисперсионной среде. Дисперсность, во многом определяющая свойства эмульсии, характеризуется тремя величинами: 1 – диаметр капелек ( ); 2 – собственно дисперсность ( ), под которой понимают величину обратную диаметру капель дисперсной фазы; 3 – удельная межфазная поверхность ( ), под которой понимают отношение суммарной поверхности капелек дисперсной фазы в единице объёма эмульсии к общему их объёму.

Все три названных величины взаимосвязаны следующим соотношением:

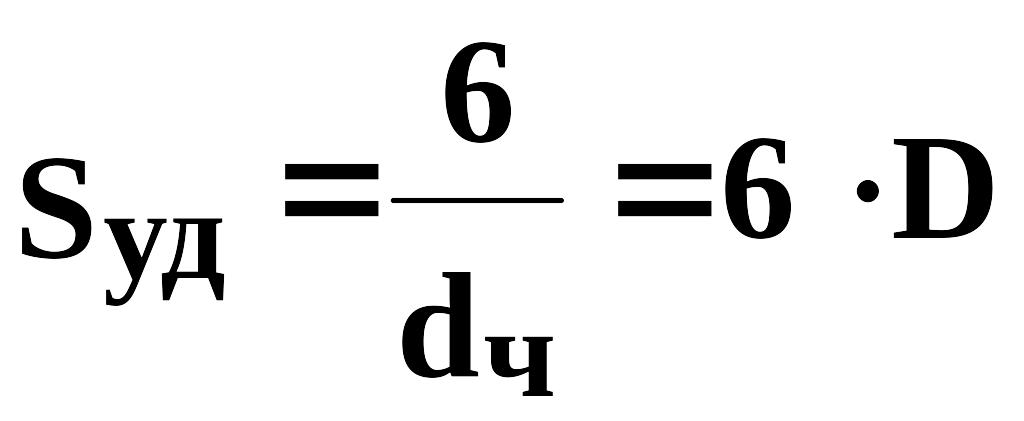(825)

Дисперсные системы, состоящие из капелек одного и того же размера, называются монодисперсными, а дисперсные системы, состоящие из капель разного диаметра, называются полидисперсными.

Первые встречаются крайне редко. Типичное распределение дисперсной фазы по диаметрам для водо – нефтяных эмульсий приведено в табл.48.

Таблица 48

Усреднённое распределение дисперсной фазы по диаметрам для водо – нефтяных эмульсий

Ø, м.10-6	3	4	5	10	20	30	40	50	60	80	100	200
	0,05	0,15	0,20	0,18	0,15	0,08	0,05	0,03	0,03	0,02	0,02	0,04

Если превышает 10^-6 м (капельки видны в оптический микроскоп), то подобные системы микрогетерогенными. Если < 10^-6 м (капельки не видны в оптический микроскоп), то подобные системы называют ультрамикрогетерогенными.

Основными параметрами, определяющими степень дисперсности водо – нефтяных эмульсий ( ) являются: скорость потока ( ), величина поверхностного натяжения на границе раздела фаз ( ), а так же частота и амплитуда пульсаций давления – так называемый масштаб пульсаций ( ).

Названные величины связаны следующим соотношением А.Н.Колмогорова:

(826)

где: - коэффициент, учитывающий соотношение вязкостей внутренней и внешней фазы;

- плотность внешней фазы.

б) Вязкость эмульсии, в основном, определяется вязкостью дисперсионной среды ( ), температурой, концентрацией дисперсной фазы ( ) и степенью её дисперсности и не является аддитивной величиной.

Существует множество формул для расчета вязкости эмульсий, взятых при определённой температуре.

Например:

Формула Эйнштейна:

(827)

которая справедлива при 15 % об.;

Формула Броутона – Сквайрса:

(828)

где: и - константы, устанавливаемые опытным путём.

Данная формула справедлива при 50 % об.

Неплохие результаты даёт формула Монсона:

(829)

которая справедлива при 70 % об.

Для прямых и обратных водо – нефтяных эмульсий зависимость вязкости от концентрации дисперсной фазы приведена на рис.135.

Рис.135. Зависимость вязкости водо – нефтяных эмульсий от содержания

дисперсной фазы

1,2 – обратная эмульсия; 3,4 – прямая эмульсия. 1,3 - эмульсия при температуре t₁; 2,4 – эмульсия при температуре t₂, причём, t₂ > t₁. - точка инверсии обратной или прямой эмульсии.

Для обратных и прямых эмульсий зависимость вязкости от температуры обратно пропорциональна.

Для обратных эмульсий вязкость в диапазоне концентраций дисперсной фазы от 0 до 40 % об. увеличивается ~ в 3 раза, а для прямых эмульсий ~ в 50 раз, но абсолютные значения вязкости для обратных эмульсий всегда существенно выше чем для прямых при одних и тех же значениях концентрации дисперсной фазы.

Для обратных эмульсий в районе концентраций дисперсной фазы порядка 74,6 % об. происходит самопроизвольное превращение эмульсии в прямую. Данная точка получила название – точка инверсии фаз обратных эмульсий ( ). Вязкость эмульсии, непрерывно нараставшая до этого, начинает стремительно убывать.

Для прямых эмульсий точка инверсии ( ) выражена менее отчетливо и находится в более широком интервале концентраций дисперсной фазы: от 0,35 до 0,45. После инверсии фаз вязкость эмульсии сначала резко нарастает, практически сравниваясь с вязкостью обратных эмульсий, а затем плавно убывает, превышая по абсолютным значениям обратные эмульсии.

в) Плотность эмульсии ( ) подчиняется правилу аддитивности и может быть рассчитана по формуле:

(830)

где: - плотность дисперсионной среды;

- плотность дисперсной фазы.

г) Электрические свойства эмульсии определяются электрическими свойствами её компонентов и её строением. Так, нефть и вода в чистом виде являются хорошими диэлектриками и имеют проводимость от 10^-12 до 10^-17 (Ом^. м)^-1 и от 10^-9 до 10^-10 (Ом^. м)^-1 соответственно.

Однако, при растворении в воде солей, она становится проводником второго рода, поэтому прямые водо – нефтяные эмульсии относятся к проводникам, а обратные к диэлектрикам, способным при наложении электрического поля в 40 – 100 раз увеличивать электропроводимость благодаря особенности поведения водяных капелек дисперсной фазы, выстраивающихся в цепочки вдоль силовых линий поля.

д) Под устойчивостью эмульсий понимают их способность сопротивляться расслоению на составляющие фазы.

Устойчивость эмульсии определяется временем её существования ( ):

(831)

где: - высота слоя эмульсии;

- средняя линейная скорость расслоения.

Поскольку любая система согласно 2-го начала термодинамики всегда стремится к минимуму свободной энергии водо – нефтяные эмульсии представляют собой термодинамически неустойчивые образования, стремящиеся к саморазрушению. Причём, с ростом температуры поверхностное натяжение всегда уменьшается, в следствии ослабления сил молекулярного притяжения. Обусловленного увеличением среднего расстояния между молекулами. Известно так же, что чем больше взаимо растворимы жидкости, образующие эмульсию, тем меньше поверхностное натяжение.

3. Пены

Пены обычно являются грубодисперсными высококонцентрированными системами, т.к. разбавленные системы относят к газовым эмульсиям.

Все пены обычно характеризуют так называемой кратностью (к) под которой понимают отношение объёма пены к объёму дисперсионной среды.

Различают низкократные пены (к изменяется от 3 до нескольких десятков) и высокократные пены (к изменяется от сотен до нескольких тысяч).

Кроме этого, пены подразделяют на малоустойчивые и высокостабильные. Первые, называемые так же динамическими, существуют только при непрерывной подаче газа в жидкость, содержащую пенообразователи 1 рода (по П.А.Ребиндеру) – например, низшие спирты и органические кислоты. Вторые могут существовать десятки минут и даже часы, особенно при добавлении пенообразователей 2 рода, например, синтетических ПАВ.

Для высокократных пен характерна ячеистая структура, в которой заполненные газом ячейки разделены тонкими плёнками жидкости. Три плёнки, расположенные под углом 120⁰ сливаются в канал, а четыре канала с углом между ними около 109⁰ образуют узел. Наиболее типичной формой ячейки в монодисперсной пене является пентагональный додекаэдр.

В низкократной пене форма ячеек близка к сферической и размер плёнок мал.

4. Пыли и туманы

Различают конденсационные, диспергационные и смешанные пыли. Первые образуются путём конденсации пара или агдезии частиц, вторые в результате измельчения.

Дисперсионная среда характеризуется: химическим составом, температурой, давлением, степенью ионизации, параметрами внешних физических полей, полями скоростей течения, наличием турбулентности и её параметрами, наличием и величиной градиентов температуры и концентрации компонентов, а так же плотностью и вязкостью.

Дисперсная фаза характеризуется: объёмной (массовой) долей, числом частиц в единице объёма (счетная концентрация), средним размером частиц, их электрическим зарядом, распределением по размерам, а так же плотностью.

Взаимодействие между дисперсной фазой и дисперсионной средой определяется процессами переноса: массы, энергии, импульса, электрического заряда, а так же процессами на границе раздела фаз.

Процессы переноса описываются уравнениями, кончный вид которых зависит от числа Кнудсена ( ):

(832)

где: - длина свободного пробега газовых молекул;

При << 1 ( >> ) дисперсионная среда может рассматриваться как сплошная, а процессы переноса происходят в континуальном режиме.

При >> 1 ( << ) пыль можно рассматривать как смесь двух газов, молекулы одного из которых намного тяжелее другого. Процессы переноса в этом случае описываются газо кинетической теорией.

При 1 процессы переноса описываются приближенными методами динамики разряженных газов.

Все виды пыли характеризуются: способностью частиц сохраняться во взвешенном состоянии, перемещаться преимущественно как единое целое и при столкновении прилипать друг к другу или поверхности.

а) В покоящейся среде частицы сохраняются во взвешенном состоянии благодаря их собственному тепловому движению и в следствии обмена энергией с молекулами дисперсионной среды. Энергия первой составляющей ( ) для частиц любой массы оценивается уравнением:

(833)

где: - постоянная Больцмана;

- абсолютная температура.

Распределение частиц по высоте обычно характеризуется так называемой Перреновской высотой ( ), определяемой по формуле:

(834)

где: - средняя масса частицы.

Для достаточно малых частиц, когда >> первой составляющей вполне достаточно для поддержания частиц во взвешенном состоянии, даже при отсутствии дисперсионной среды.

А вот если << , то для поддержания частиц во взвешенном состоянии необходима вторая составляющая, т.е. дополнительная энергия ( ), получаемая при соударении частиц дисперсной фазы с молекулами дисперсионной среды.

Соотношение между двумя этими видами энергии характеризуется числом Шмидта:

(835)

где: - концентрация газовых молекул.

Так вот, при < 10^-7 существенен лишь вклад теплового движения.

При > 10^-5 имеет значение лишь обмен энергией между частицами и средой.

При 10^-7< < 10^-5 оба вклада соизмеримы.

В движущейся газовой среде частицам аэрозоля присущи две основные формы движения – увлечение дисперсионной средой и смещение относительно её. Поддержка частиц во взвешенном состоянии в этом случае определяется их инерционностью и характеризуется так называемым турбулентным числом Шмидта ( ) – равным отношению коэффициента турбулентной диффузии частиц ( ) к коэффициенту турбулентной диффузии молекул среды ( ).

Кроме энергии теплового движения частиц, обмена энергией между частицами и средой и энергии, поступающей извне, аэрозольные частицы могут поддерживаться во взешенном состоянии за счет градиентов температуры и концентрации. Возникающие при этом движения носят названия термо – и диффузио – фореза соответственно.

Однако, аэрозольные системы не могут существовать вечно. При прекращении поступления энергии извне, выравнивании температурных и концентрационных полей и установлении равновесия между тепловой энергией частиц и среды неизбежно начнется процесс самопроизвольного оседания частиц, не способных в силу своей массы удержаться во взвешенном состоянии за счет теплового движения при данных термобарических параметрах. При этом, на скорость коагуляции влияет наличие электрического заряда на частицах и наличие внешнего электрического поля. Аэрозольные частицы способны приобретать электрический заряд многими способами, например, если они образуются конденсацией на ионах. Не заряженные частицы могут захватывать газовые ионы. Наконец, частицы приобретают заряд при освещении, облучении, прохождении коронного разряда и т.п.

1.2. Теоретические основы гравитационного разделения фаз

1.2.1. Осаждение одиночной сферической твёрдой частицы в неподвижной жидкости.

На такую частицу будут действовать три силы:

Веса ( ):

(836)

Подъёмная сила Архимеда ( ):

(837)

Сила сопротивления жидкости равноускоренному оседания частицы – закон Ньютона – ( ):

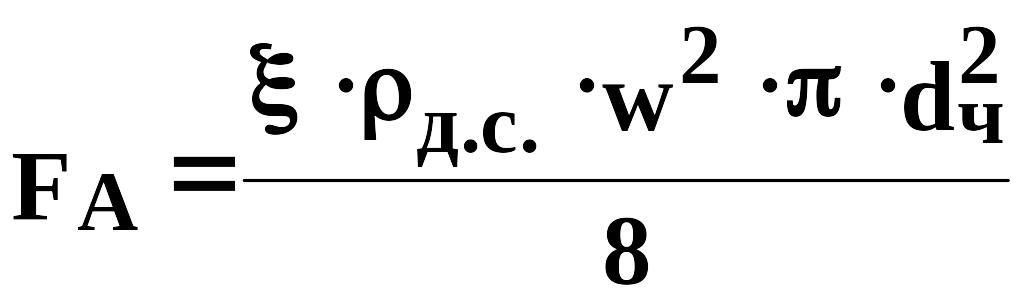(838)

где: - безразмерный коэффициент сопротивления среды;

- нарастающая скорость оседания частицы.

Т.к. частица оседает под действием разности постоянных сил ( ) и ( ), то она будет двигаться равноускоренно. Но, с ростом скорости оседания немедленно увеличивается сила сопротивления жидкости и, в результате, после короткого участка равноускоренного движения дальнейшее оседание будет происходить с постоянной скоростью ( ) под действием следующего баланса сил:

(839)

или:

(840)

Откуда, скорость осаждения:

(841)

Однако, в соответствии с терминологией гидравлики, любое движение (в данном случае частицы) происходит либо в ламинарном, либо в турбулентном, либо, наконец, в переходном режиме.

При ламинарном оседании (мелкие частицы или большая вязкость жидкости) сопротивление среды определяется только силами трения.

При турбулентном оседании (крупные частицы или малая вязкость жидкости) сопротивление среды определяется образованием турбулентных вихрей.

При переходном оседании сопротивление среды определяется и силами трения и образованием турбулентных вихрей.

Границы между названными режимами определяются численными значениями критерия Рейнольдса:

(842)

Ламинарному режиму соответствует: < 0,2 ÷ 2

Турбулентному режиму соответствует: 500

Переходному режиму соответствует: 0,2 ÷ 2 < 500

Для нахождения ( ) по уравнению (841) необходимо знать ( ), но , т.е. согласно уравнения (842) в свою очередь зависит от ( ).

Поэтому, приходится задаваться режимом осаждения, а после определения ( ) проводить проверку, вычисляя , т.е. вести расчет методом последовательного приближения.

Однозначно решить эту задачу можно пользуясь критериальным уравнением отстаивания, для вывода которого прежде всего выразим коэффициент сопротивления ( ) из уравнения (840):

(843)

После умножения обоих частей равенства на получим:

(844)

или:

(845)

Величина:

(846)

носит название критерия Архимеда и в него входят только известные величины.

Тогда:

(847)

или:

(848)

Но если критерий Рейнольдса будет найден, то из уравнения (842) легко найти искомую скорость осаждения:

(849)

Так вот, при ламинарном режиме ( 36 ):

(850)

Тогда, подставляя выражение (850) в (847) получим:

(851)

Подставим это выражение в уравнение (849), раскроем критерий Архимеда согласно (846) и получим окончательное выражение для скорости осаждения одиночной сферической частицы в покоящейся жидкости при ламинарном режиме осаждения:

(852)

При турбулентном режиме ( 82500):

0,44 (853)

Тогда, подставляя выражение (853) в (847) получим:

(854)

Подставим это выражение в уравнение (849), раскроем критерий Архимеда согласно (846) и получим окончательное выражение для скорости осаждения одиночной сферической частицы в покоящейся жидкости при турбулентном режиме осаждения:

(855)

При переходном режиме (36 < < 82500):

(856)

Критерий Рейнольдса можно вычислить и без знания коэффициента сопротивления, если воспользоваться выражением, пригодным для всех режимов осаждения:

(857)

При ламинарном течении вторым слагаемым в знаменателе можно пренебречь и уравнение (857) превращается в выражение (851).

При турбулентном течении первым слагаемым в знаменателе можно пренебречь и уравнение (38) принимает вид:

(858)

1.2.2. Осаждение несферической одиночной твёрдой частицы в неподвижной жидкости.

Если гравитационному разделению подвергается смесь, содержащая частицы, форма которых отличается от шарообразных, то скорость их осаждения ( ) рассчитывается по уравнению:

(859)

где: - так называемый коэффициент формы:

(860)

где: и - поверхности частиц шарообразной и неправильной формы равного объёма.

Нахождение знаменателя предполагает знание размеров и формы частицы; а нахождение величины числителя базируется на определении так называемого эквивалентного диаметра частицы:

(861)

где: - масса частицы неправильной формы;

- плотность материала частицы неправильной формы.

Поскольку нахождение достаточно проблематично, гораздо удобнее воспользоваться его следующими средними значениями для частиц различной формы:

Округлые частицы………………………. 0,77

Пластинчатые частицы………………….. 0,73

Угловатые частицы……………………… 0,66

Продолговатые частицы………………… 0,53

Иногда, при расчетах используется так называемый фактор несферичности:

(862)

Тогда:

(863)

1.2.3. Осаждение одиночной твёрдой частицы в двигающейся жидкости.

Если частица оседает в двигающейся жидкости, то приходится обращаться к векторной сущности её скорости оседания ( ):

(864)

где: - векторная величина скорости оседания частицы ( в данном случае сферической и одиночной);

- векторная величина скорости перемещения дисперсионной среды

1.2.4. Осаждение сообщества одинаковых сферических твёрдых частиц в неподвижной жидкости.

Рассмотренные случаи гравитационного разделения фаз носят название оседания в свободных условиях, т.к. оседающая частица либо одинока, либо их концентрация настолько мала, что вероятность их взаимодействия при оседании равна нулю.

Оседание частиц в среде с их высокой концентрацией, когда их взаимодействие (и прежде всего соударения) становится неизбежным, называется оседанием в стеснённых условиях. Подобные условия реализуются, если 5 % об. Причём, находится как среднее арифметическое между и .

В этом случае, критерий Рейнольдса можно найти по уравнению:

(865)

где: - относительная доля дисперсионной среды в исходной смеси:

(866)

где: - объём дисперсионной среды;

- объём дисперсной фазы.

Тогда, окончательное выражение для скорости осаждения сферической частицы в неподвижной жидкости в стесненных условиях при любых режимах движения будет иметь вид:

(867)

Экспериментальными исследованиями установлена следующая связь между скоростью оседания в свободных и стесненных условиях:

(868)

где: - эмпирический коэффициент, величину которого в практических расчетах можно принять равной 4,7.

Известны так же зависимости:

(869)

(870)

Первая справедлива при > 0,7; вторая при 0,7

Иногда, вместо критерия Архимеда используют критерий Галилея (Ga), взаимосвязь между которыми определяется уравнением:

(871)

А вместо критерия Рейнольдса используют критерий Лушенко (Ly), взаимосвязь между которыми определяется уравнением:

(872)

Графически взаимосвязь критериев Рейнольдса, Архимеда и Лушенко проиллюстрирована номограммой на рис.136.

(ВСТАВКА 3 часть)

2. Технологический расчет отстойной аппаратуры

Технологический расчет отстойной аппаратуры заключается в определении пропускной способности отстойника или его размеров.

2.1. Расчет пропускной способности.

2.1.1. Прикидочный (приближенный расчет).

Первое допущение: температура во всех точках гравитационного аппарата одинакова, т.е. конвекционные токи отсутствуют.

Второе допущение: скорость движения частиц дисперсной фазы постоянна в любой момент времени и в любой точке траектории.

Третье допущение: частицы дисперсной фазы сферичны.

Четвёртое допущение: скорость течения эмульсии в аппарате не влияет на скорость осаждения частиц дисперсной фазы.

Рассмотрим только горизонтальный или вертикальный двухфазный отстойник (схемы которых приведены на рис.137 и 138), в котором происходит гравитационное разделение эмульсии типа В/Н.

Рис.137. Схема горизонтального отстойника.

Р ис.138. Схема вертикального отстойника.

1. Зная и с помощью табл.3 определяют минимальный размер капель дисперсной фазы , которые удаляются в данном отстойнике.

Для этого, вычисляют как разницу и и двигаясь справа налево по нижней строке таблицы суммируют указанные в ячейках величины до тех пор пока найденное слагаемое не станет равным (или минимально не превысит) . Соответствующее значение и будет искомым .

2. По формуле (846) рассчитывают критерий Архимеда, заменяя на .

3. В зависимости от численного значения критерия Архимеда рассчитывают скорость свободного осаждения одиночной частицы дисперсной фазы либо по формуле (852), либо (855), либо, наконец, по формуле (856).

4. При необходимости, скорость свободного оседания пересчитывают на стесненные условия, для чего пользуются либо формулой (867) – заменяя на ; либо формулами (868) – (870).

5. Рассчитывают объёмную пропускную способность отстойника по исходной эмульсии :

(873)

где: - средняя скорость движения эмульсии в аппарате;

- часть площади сечения аппарата, занятая нефтью.

Для горизонтального отстойника:

Если эмульсия подаётся под водяную подушку:

(874)

Если эмульсия подаётся выше водяной подушки:

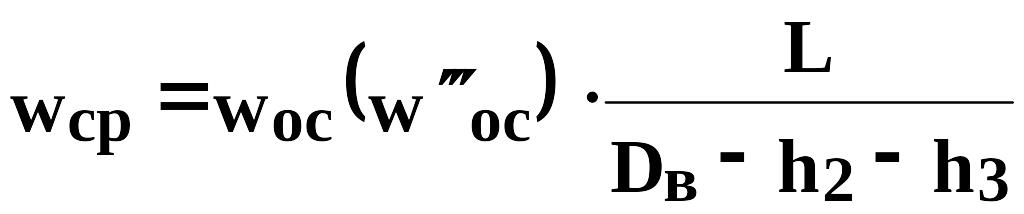(875)

(876)

где:

(877)

(878)

Для вертикального отстойника:

(879)

(880)

2.1.2. Точный расчет (на примере горизонтального отстойника с подачей эмульсии под водяную подушку).

Расчет базируется на ряде следующих положений качественно описывающих реальную картину гравитационного осаждения полидисперсной эмульсии типа В/Н в стесненных условиях в двигающейся жидкости.

1. За время прохождения эмульсии от входа до выхода отстойника концентрация дисперсной фазы изменяется как вдоль аппарата, так и по его высоте.

По горизонтали она уменьшается от входа к выходу.

По вертикали она возрастает от верхней границы жидкости в аппарате к границе водяной подушки.

2. За время прохождения эмульсии от входа до выхода отстойника её вязкость изменяется как вдоль аппарата, так и по его высоте.

По горизонтали она уменьшается от входа к выходу.

По вертикали она возрастает от верхней границы жидкости в аппарате к границе водяной подушки.

3. За время прохождения эмульсии от входа до выхода отстойника её линейная скорость изменяется как вдоль аппарата, так и по его высоте.

По горизонтали она уменьшается от входного значения :

(881)

до выходного значения :

(882)

где: - объёмный расход отводимой нефти с оставшейся обводненностью.

По вертикали она уменьшается от верхней границы жидкости в аппарате к границе водяной подушки.

Такой сложный характер поведения реальной эмульсии в аппарате неизбежно требует ряда упрощений:

1. Пренебрежем толщиной входного слоя, который образуется между нефтью и водяной подушкой.

2. Будем вести расчет, используя понятие .

3. Будем считать время отстоя равным среднему времени движения эмульсии вдоль зоны отстоя.

Тогда:

(883)

Откуда:

(884)

Но из уравнения (881) следует, что:

(885)

но:

(886)

Откуда:

(887)

или, с учетом выражения (882):

(888)

Подставим выражение (888) в (885) и получим:

(889)

Известно, что из материального баланса работы отстойника, пренебрегая захватом нефти дренажной водой, можно записать, что:

(890)

Подставим выражение (890) в уравнение (889) и выразим из полученного равенства :

(891)

Подставим в уравнение (891) значение из уравнения (884) и получим выражение:

(892)

Дальнейшее преобразования возможны по нескольким направлениям.

1 Направление.

На основании уравнения (864) можно записать, что:

(893)

Первый слагаемый вектор направлен вертикально вниз, а его модуль после замены на и на согласно выражения (867), пригодного для всех режимов осаждения приобретает вид:

(894)

Второй слагаемый вектор направлен горизонтально, а его модуль может быть определён по уравнению:

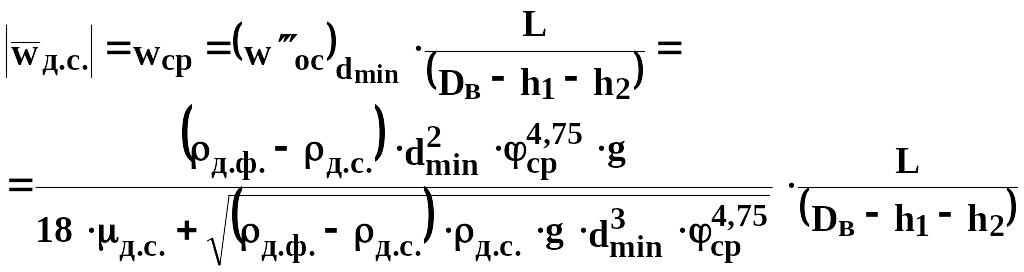(895)

Подставим уравнение (894) и (895) в выражение (892) и получим итоговое соотношение:

(896)

2 Направление.

Вновь используют исходное выражение (893), но при нахождении модульных значений слагаемых векторов используют либо выражение (868), либо (869), либо, наконец, (870).

Допустим, было выбрано самое общее выражение (868); тогда модуль первого слагаемого (после замены на ) можно найти по выражению:

(897)

А модуль второго слагаемого можно выразить следующим образом:

(898)

Величина в зависимости от режима оседания может быть определена либо по уравнению (852), либо (855), либо, наконец, (856). При этом, разумеется, заменяется на .

Допустим, оседание происходит в ламинарных условиях, тогда подставив выражение (852) в формулы (897) и (898), а затем подставив полученные выражения в формулу (892), получим итоговое соотношение для ламинарных условий оседания:

(899)

Аналогично, для оседания в турбулентных условиях получим:

(900)

При переходном режиме (901):

3 направление:

Данный подход основан на выражении:

(902)

Тогда, по аналогии, итоговое уравнение для ламинарных условий оседания примет вид (903):

Для турбулентных условий оседания:

(904)

При переходном режиме:

(905)

Расчет вертикального отстойника принципиально не отличается от горизонтального за тем лишь исключением, что в итоговых формулах (896), (899), (900), (901), (903), (904) и (905) вместо используется выражение , а вместо используется .

Если водо – нефтяная эмульсия подаётся выше водяной подушки, то вместо выражения используется выражение , а вместо выражения используется выражение для соответствующих типов отстойников.

2. Расчет геометрических размеров отстойников.

   1. Определение диаметра (на примере вертикального отстойника –рис. 139, 140.)

Р ис.139. Схема вертикального отстойника с газовой подушкой.

Диаметр отстойника определяют исходя из объёма поступающего в него продукта. Если в отстойнике одновременно отделяется газ, то величину сечения рассчитывают и по газовому и по жидкостному потоку, а затем, по большему значению и определяют внутренний диаметр, который в данном случае является минимально необходимым.

Минимально необходимую площадь сечения по газовому потоку рассчитывают следующим образом:

1. Определяют предельно допустимую скорость газового потока ( ) по формуле Обрядчикова – Хохрякова:

(906)

2. Определяют объёмный расход газа ( ):

(907)

где: Т – температура в отстойнике, К;

Р – давление в системе, МПа;

G_i – массовый расход i – го компонента, кг/час;

M_i – молекулярная масса i – го компонента.

Р ис. 140. Схема вертикального отстойника без отделения газа

3. Определяют площадь сечения:

(908)

Минимально необходимую площадь сечения по жидкостному потоку рассчитывают следующим образом:

(909)

где: Q_э – объёмный расход эмульсии;

u_э – предельно допустимая скорость жидкостного потока.

При этом:

(910)

Обычно u_э не превышает 0,002 – 0,005 м/с (из опытных данных).

Искомый диаметр аппарата определяют по формуле:

(911)

Если аппарат имеет отбойную перегородку, то расчет необходимо вести по наиболее узкому месту, т.е. по площади сегмента MEN.

В этом случае формула (908) дает нам величину не S_г, а S_c т.е. необходимую площадь сегмента, пересчитать которую на внутренний диаметр можно по формуле:

(912)

2. Определение высоты отстойника

Высоту отстойника с газовой подушкой рассчитывают следующим образом:

1. Вначале находят высоту зоны отстоя (Н_от), задаваясь длительностью отстоя ( ) – из опытных данных обычно принимают исходя из диапазона 20 – 60 мин.:

(913)

Высота h₁ обычно принимается равной примерно 0,7^.Н_от, а величину находят из уравнения:

(914)

2. Высоту уровня водяной подушки (Н_в) можно принять равной 0,5 – 0,6 м, если имеется автоматический регулятор её уровня; при его отсутствии 1 м.

3. Высоту расположения штуцера вывода воды ( 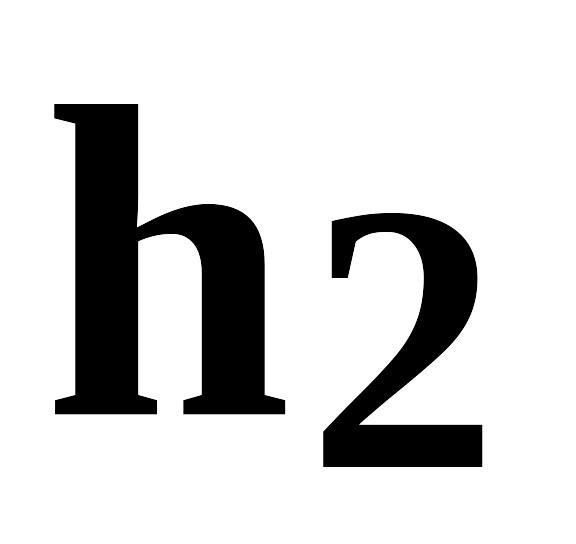) можно принять равной 0,3 – 0,4 м.

4. Высоту слоя чистой нефти (Н_н) необходимо принимать такой, чтобы предотвратить попадание в неё капель воды:

(915)

где: - массовый расход конденсата;

- плотность конденсата.

Обычно, этот расчет не проводят, а просто принимают 0,5 м.

5. Высоту h₃ определяют исходя из 10 минутного количества орошения.

6. Высоту h₄ обычно принимают равной 0,4 – 0, 5 м. При выводе нефти самотеком h₄ = 0.

7. Высоту h₅ обычно принимают равной 0,4 м; а высоту h₆ равной 0,6 м (для предотвращения переброса жидкости через сливную перегородку).

8. Высоту свободного пространства под отбойником h₇ находят по уравнению:

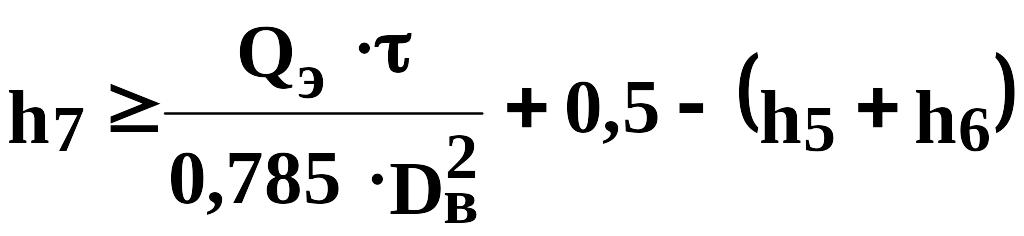(916)

Обычно этого расчета не проводят, а просто принимают h₇ 0,5 м.

9. Высота h₈ зависит от конструкции аппарата. Если ставят отбойные тарелки, то h₈ зависит от их число (n) и расстояния между ними (а), т.е.:

(917)

Если тарелок нет, то обычно принимают h₈ = 0,6 м.

10. Высоту свободного пространства над отбойником (h₉) обычно принимают равной 0,5 м.

Общая высота цилиндрической части отстойника (Н):

(918)

Если газовая подушка отсутствует, то обычно принимают:

H_п = 0,8 м.