- •1 Проектування привода
- •1.1 Завдання і обґрунтування. (Завдання 2) Складові частини привода:
- •1.2 Вибір електродвигуна, кінематичний та енергетичний розрахунок привода.
- •1.3 Розрахунок передачі редуктора
- •1.3.1 Вибір матеріалів і розрахунок допустимих напружень
- •1.3.2 Допустимі контактні напруження
- •1.3.3 Допустимі напруження на згин
- •1.3.4 Проектування конічної зубчастої передачі
- •1.3.9 Сили у зачепленні.
- •1.3.10 Питома колова сила.
- •1.3.11 Перевірка міцності передачі на контактну втому.
- •1.3.3 Визначити швидкість ланцюга
- •1.3.4 Визначити міжосьову відстань
1.3.3 Допустимі напруження на згин
У
розрахунках зубців на втому при згині
допустиме напруження визначаємо окремо
для зубців шестерні
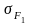 і колеса
і колеса
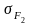 за
формулою:
за
формулою:
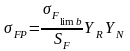
де
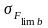 - границя витривалості при згині, що
відповідає базі випробувань NFO
=
4106,
при коефіцієнті асиметрії R=0
і визначається за рекомендаціями
табл.3.7:
- границя витривалості при згині, що
відповідає базі випробувань NFO
=
4106,
при коефіцієнті асиметрії R=0
і визначається за рекомендаціями
табл.3.7:
для
шестірні
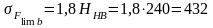 МПа;
МПа;
для
колеса
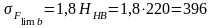 МПа.
МПа.
Коефіцієнт
довговічності визначається за формулою:
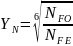
де NFE - еквівалентне число циклів зміни напружень згину за термін служби передачі (μF = 0.065 для режиму СН та значенні m=6):
NFE1 = μF NΣ1 = 0,06585,77107= 5.575107
NFE1 = μF NΣ2 = 0,06521,44107= 1.3107
NHO = 4⋅106, при коефіцієнті асиметрії R=0;
Звідси:
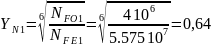
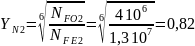
Так як NFO<NFE, то беремо YN1=YN2=1.
Допустимі напруження згину, при коефіцієнті запасу міцності SF =2 і коефіцієнті шорсткості перехідної поверхні для шестерні і колеса (поліпшення) YR2=1,2
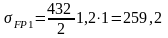 МПа;
МПа;
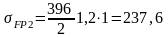 МПа.
МПа.
Граничні допустимі напруження на згин:
Для
шестірні
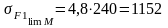 МПа;
МПа;
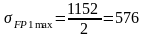 МПа.
МПа.
Для
колеса
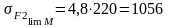 МПа;
МПа;
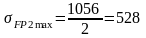 МПа
МПа
1.3.4 Проектування конічної зубчастої передачі
Вихідними даними для проектного розрахунку передачі є такі:
- крутний момент на валу шестірні Т1=25,42 Hм;
- передаточне число передачі u= 4;
- матеріал зубчастих коліс та їх термообробка, твердість активних поверхонь.
- коефіцієнт ширини вінця зубчастого колеса ψba = b / aw або ψbd = b / d1 (приймаємо ψba = 0,315 [Таблиця 3.8]) ;
- типовий режим роботи передачі та строк її служби (режим - CH, h=10000 годин);
1.3.5 Зовнішній ділильний діаметр.
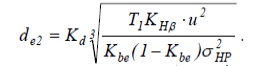
Кd=1000 МПа1/3 – для стальних коліс;
Коефіцієнт ширини зубчастого вінця Kbe = 0,25
Kbd = Kbe·u/(2- Kbe) = ·0.25·4/(2-0.25) = 0.571
Нерівномірність розподілу навантаження враховується коефіцієнтом KHβ, значення якого визначаються за табл.4.1. Вибираємо значення методом інтерполяції.
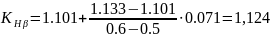
Підставляємо значення і шукаємо dе2:
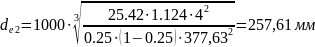
1.3.6Число зубців шестірні і колеса.
Зі загальної умови z1 ≥zmin= 17 та виконуючи умову z1 + z2 ≤ 80…85. підбираємо значення z1:
z1 = 17; z2 = u· z1 = 68;
Уточнювати передаточне число u не потрібно, так як не відбувалося заокруглень у визначенні числа зубців.
1.3.7Модуль зубців зубчастих коліс.
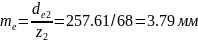
Модуль зубців потрібно узгодити з стандартним значенням із таблиці 3.10
Приймаємо
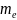 = 4 мм
= 4 мм
Фактичний зовнішній ділильний діаметр:
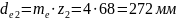
1.3.8 Визначення геометричних розмірів шестірні і колеса.
Нагадаємо
базові параметри вихідного контуру.
Кут профілю α=20°;
коефіцієнт висоти головки зубця,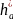 =1, коефіцієнт висоти ніжки зубця
=1, коефіцієнт висоти ніжки зубця
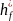 =1,2;
коефіцієнт радіального зазору с*= 0,2.
=1,2;
коефіцієнт радіального зазору с*= 0,2.
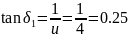
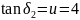
Звідси
кути рівні
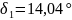 ;
;
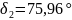
Зовнішня
висота головки зубця:
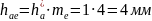
Зовнішня
висота ніжки зубця:
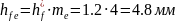
Зовнішня
висота зубця:
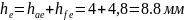
Розміри
вінців конічних коліс:
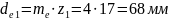
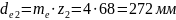
Зовнішні
діаметри вершин зубців:
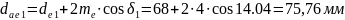
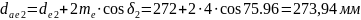
Зовнішня конусна відстань:
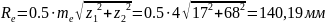
Ширина зубчастого вінця:
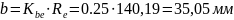
Округлюємо до найближчого цілого парного числа:
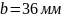
Середній коловий модуль зубців:
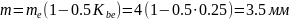
Cередні ділильні діаметри:
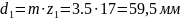
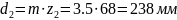
Кути головки, θа та ніжки, θf зубця:
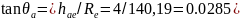
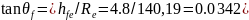
Звідси:
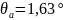 ;
;
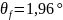
Кути конуса вершин зубців шестірні і колеса:
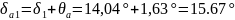
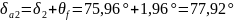
Кути конуса западин зубців:
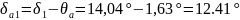
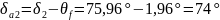
Модуль зубців еквівалентних коліс mv = m = 3.5 мм
Ширина вінця еквівалентної передачі bv = b = 36 мм
Ділильні діаметри еквівалентних циліндричних коліс:
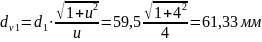
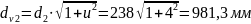
Число зубців еквівалентних коліс:
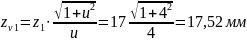
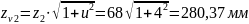
Передаточне число:
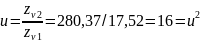
Коефіцієнт перекриття у прямозубій конічній передачі: