Контрольная работа по логике
1. Из хорошо известной Вам области знаний выберете некоторое понятие G и дайте его логический анализ: укажите его вид, содержание, виды признаков, составляющих его содержание, укажите его объем и элементы объема. Дайте определение G через ближайший род и видовое отличие. Осуществите деление G по видоизменению признака. Приведите логические аргументы в пользу того, что Ваши определение и деление выполнены правильно. Укажите понятия, которые с G (вместо G можно выбрать другое понятие) находятся в отношении: подчинения, соподчинения, пересечения, контрарности, контрадикторности. Изобразите эти отношения кругами Эйлера.
Выбрали понятие G – «телефон».
Понятия, используемые в науке и в других сферах человеческой деятельности, чрезвычайно многообразны по своей структуре, типам обобщаемых в них объектов и другим характеристикам. Типологизация понятий, т.е. выделение и систематизация различных их видов, может проводиться по разным основаниям - их делят на виды, во-первых, исходя из особенностей содержаний, и во-вторых, учитывая специфику их объемов и элементов объемов.
В зависимости от характера признака, посредством которого осуществляется обобщение объектов в понятии, они делятся на простые (их содержание указывает на присущность или неприсущность отдельного свойства, напр., "разумное существо") и сложные (их содержание фиксирует связь между свойствами, напр., "существо, способное летать и плавать"), на безотносительные (объект характеризуется сам по себе, напр., "древний город") и относительные (объект характеризуется через отношение к другим объектам, напр., "город, расположенный южнее Москвы").
По количеству элементов объема различают пустые понятия (не содержащие элементов объема) и непустые понятия (объем которых имеет по крайней мере один элемент). Понятие может оказаться пустым по разным причинам: во-первых, в силу сложившихся обстоятельств (напр., "король, правивший во Франции в XX веке") или в силу законов природы (напр., "вечный двигатель"), такие понятия называют фактически пустыми; во-вторых, в силу логической противоречивости его содержания (напр., "режиссер, поставивший все пьесы Чехова и не поставивший чеховской Чайки"), их называют логически пустыми.
Непустые понятия бывают единичными (их объем содержит ровно один элемент) и общими (объем содержит более одного элемента), а общие делятся на регистрирующие и нерегистрирующие (в зависимости от того, поддается ли на практике точному подсчету количество элементов их объемов).
На основании отношения объемов понятий к их родам (универсумам) выделяют универсальные и неуниверсальные понятия (объемы первых совпадают с родом, у вторых они уже рода). Различают фактически и логически универсальные п. Объемы первых совпадают с родом в силу обстоятельств нелогического характера (напр., "металл, проводящий тепло"), содержания вторых - логически необходимые признаки, логическая форма которых является общезначимой формулой (напр., "человек, который сильнее всех или не сильнее кого-нибудь").
По структуре
элементов объема различают несобирательные
понятия, элементами объемов которых
являются отдельно взятые объекты (напр.,
"человек, родившийся в 1900 году" или
их кортежи - пары, тройки и т.д. (напр.,
"люди, родившиеся в одном и том же
году", подобные понятия имеют вид
),
и собирательные
понятия, их элементами объема являются
совокупности объектов, мыслимые как
одно целое (напр., "политическая
партия").
Понятие «телефон» - непустое, общее, конкретное, собирательное, относительное, положительное.
Обобщение некоторого понятия есть операция образования из этого понятия некоторого нового с более широким объемом, что означает обобщение и выделение более широкого круга предметов. Обратная операция перехода от некоторого понятия к понятию с меньшим объемом называется ограничением понятия.
Переход от данного понятия к понятию с более широким объемом — обобщение понятия — осуществляется за счет определенного ослабления содержания первого. Так, от понятия «повествовательное предложение» переходим к понятию «предложение», исключая из содержания этого понятия указание на то, что в грамматической форме этого типа о чем-то сообщается.
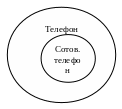
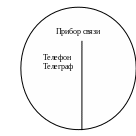
Обобщение понятия «телефон» - понятие «прибор связи», ограничение рассматриваемого понятия – понятие «сотовый телефон».
Рассматривая отношения между понятиями, следует всего различать понятия сравнимые и несравнимые.
Сравнимыми называются понятия, имеющие некоторые признаки, позволяющие эти понятия сравнивать друг с другом. Например, «пресса» и «телевидение» — сравнимые понятия, они имеют общие признаки, характеризующие средства массовой информации.
Несравнимыми называются понятия, не имеющие общих признаков, поэтому и сравнивать эти понятия невозможно. Например:«квадрат» и «общественное порицание», «преступление» и «космическое пространство», «государство» и «симфоническая музыка» Они относятся к разным, весьма отдаленным друг от друга областям действительности и не имеют признаков, на основании которых их можно было бы сравнивать друг с другом. В логических отношениях могут находиться только сравнимые понятия.
1. Подчинение
2. Соподчинение
3. Пересечение
4. Контрарность
5. Контрадикторность
2. Из хорошо известной Вам области знаний подберите содержательный пример простого категорического (атрибутивного) суждения вида А (по логическому квадрату). Укажите составляющие его элементы: кванторное слово, субъект, предикат, субъектно-предикатную связку. Сформулируйте другие простые категорические суждения, которые с А находятся в отношении: подчинения (I), контрадикторности (О), контрарности (Е). Укажите истинностные значения I, О, Е для двух истинностных значений А. Дайте анализ распределености терминов в рассмотренных суждениях А, I, О, Е. Осуществите в отношении выбранного Вами суждения А логические операции превращения, обращения, противопоставления предикату. Проведите анализ распределенности терминов в образовавшихся в результате этих операций суждениях.
Суждение А: Все люди – млекопитающие
Кванторное слово – все
Субъект – люди
Предикат – млекопитающие.
Субъектно-предикатная связка – есть (это слово подразумевается: Все люди есть млекопитающие).
Для понимания смысла категорических суждений полезно знать отношения между ними, которые изображаются посредством так называемого «логического квадрата». При этом имеют в виду суждения, как говорят, «с одинаковой материей», то есть с одними и теми же субъектами и предикатами:
|
По верхней горизонтали суждения типа А и Е контрарно противоположны, т.е. несовместимы по истинности: они не могут быть одновременно истинными.
По нижней горизонтали суждения типа I и О находятся в отношении «перекрещивания» (обычное название – «субконтрарность»). Они несовместимы по ложности, т.е. не могут быть одновременно ложными (но могут быть одновременно истинными).
По обеим вертикалям – отношение логического подчинения: суждение типа А подчиняет I, а I подчинено А; аналогично для суждений типа Е и О соответственно. Для этого отношения характерны два свойства:
1) если истинно общее суждение, то истинно и подчиненное ему частное;
2) если ложно частное суждение, то ложно и соответствующее ему общее.
Отношение между суждениями, находящимися в концах диагоналей, – между А и О, Е и I – отношение контрадикторной противоположности (противоречия).
Простые суждения, которые находятся с А в отношении:
подчинения (I): Некоторые люди - млекопитающие
контрадикторности (О): Некоторые люди не есть млекопитающие
контрарности (Е): Ни один человек не является млекопитающим
Операция обращения: Некоторые млекопитающие – люди
Кванторное слово – некоторые
Субъект – млекопитающие
Предикат – люди
Субъектно-предикатная связка – есть
Операция превращения: Все дельфины не есть немлекопитающие.
Кванторное слово – все
Субъект – люди
Предикат – немлекопитающие.
Субъектно-предикатная связка – не есть
Операция противопоставления предикату: Некоторые млекопитающие не есть люди.
Кванторное слово – некоторые
Субъект – млекопитающие
Предикат – люди
Субъектно-предикатная связка – не есть
3. Приведите содержательные примеры основных видов сложных суждений (по одному для каждого вида – отрицания, конъюнкции, дизъюнкции, строгой дизъюнкции, импликации, эквиваленции). Укажите составляющие их суждения. Дайте анализ истинностных значений указанных сложных суждений в функции от истинностных значений их составляющих.
Сложное суждение – суждение, образованное из простых посредством логических союзов конъюнкции, дизъюнкции, импликации, эквивалентности.
Логический союз – это способ соединения простых суждений в сложное, при котором логическое значение последнего устанавливается в соответствии с логическими значениями составляющих его простых суждений.
Особенность сложных суждений заключается в том, что их логическое значение (истинность или ложность) определяется не смысловой связью простых суждений, составляющих сложное, но двумя параметрами:
1) логическим значением простых суждений, входящих в сложное;
2) характером логической связки, соединяющей простые суждения;
Современная формальная логика отвлекается от содержательной связи между простыми суждениями и анализирует такие высказывания, в которых эта связь может отсутствовать. Например, «Если вы будете хорошо учиться, то обязательно получите диплом».
Логическое значение сложного суждения устанавливается при помощи таблиц истинности. Таблицы истинности строятся следующим образом: на входе выписываются все возможные комбинации логических значений простых суждений, из которых состоит сложное суждение. Число этих комбинаций можно высчитать по формуле: 2n, где n – число простых суждений, составляющих сложное. На выходе выписывается значение сложного суждения.
Конъюнктивное суждение – суждение, которое является истинным тогда и только тогда, когда истинны все входящие в него суждения.
Образуется посредством логического союза конъюнкции, выражающегося грамматическими союзами «и», «да», «но», «однако». Например, «Мы поедем в Санкт-Петербург и посетим Русский музей».
Символически обозначается следующим образом: А*В, где А, В – переменные, обозначающие простые суждения, *– символическое выражение логического союза конъюнкции.
Определению конъюнкции соответствует таблица истинности:
А |
В |
А*В |
И |
И |
И |
И |
Л |
Л |
Л |
И |
Л |
Л |
Л |
Л |
Дизъюнктивные суждения. Имеется два вида дизъюнктивных суждений: строгая (исключающая) дизъюнкция и нестрогая (неисключающая) дизъюнкция.
Строгая (исключающая) дизъюнкция – сложное суждение, принимающее логическое значение истины тогда и только тогда, когда истинно только одно из входящих в него суждений или «которое ложно тогда, когда оба высказывания ложны». Например, «либо A, либо B».
Логический союз дизъюнкция выражается посредством грамматического союза «либо…либо».
Символически записывается А v В.
Логическое значение строгой дизъюнкции соответствует таблице истинности:
-
А
В
А v В
И
И
Л
И
Л
И
Л
И
И
Л
Л
Л
Нестрогая (неисключающая) дизъюнкция – сложное суждение, принимающее логическое значение истины тогда и только тогда,когда истинным является, по крайней мере, одно (но может быть и больше) из простых суждений, входящих в сложное. Например, «Студенты добиваются хороших показателей в учебе или прилежанием, или систематическим повторением пройденного».
Нестрогая дизъюнкция выражается посредством грамматического союза «или…или» в разделительно-соединительном значении.
Символически записывается АvВ. Нестрогой дизъюнкции соответствует таблица истинности:
-
А
В
АvВ
И
И
И
И
Л
И
Л
И
И
Л
Л
Л
Импликативные (условные) суждения.
Импликация – сложное суждение, принимающее логическое значение ложности тогда и только тогда, когда предшествующее суждение (антецедент) истинно, а последующее (консеквент) ложно.
В естественном языке импликация выражается союзом «если..., то» в смысле«наверно, что А и не В». Например, «Если число делится на 4, то оноделится и на 2».
Символически импликация записывается А→ В (если А, то В).
Логическое значение представлено в таблице истинности:
-
А
В
А→ В
И
И
И
И
Л
Л
Л
И
И
Л
Л
И
Анализ свойств импликации показывает, что истинность антецедента является достаточным условием истинности консеквентна, но ненаоборот. Достаточным для некоторого явления считается такое условие, наличие которого непременно вызывает это явление. Например, «быть розой» достаточное условие, чтобы включить ее в класс цветов, так как все розы – цветы и ни одна не роза не является цветком.
В то же время истинность консеквентна является необходимым условием истинности антецедента, но недостаточным. Необходимым для явления считается такое условие, без которого оно (явление) не имеет место. Например, класс роз включен в класс цветов, но не равен ему. Есть цветы, которые не являются розами. Однако условие «быть цветком» для розы является обязательным, так как все розы – цветы.
Эквивалентность – сложное суждение, которое принимает логическое значение истины тогда и только тогда, когда входящие в него суждения обладают одинаковым логически значением, т. е. одновременно либо истинны, либо ложны.
Логический союз эквивалентности выражается грамматическими союзами «тогда и только тогда, когда», «если и только если». Например, «Если пудинг, о котором идёт речь, с заварным кремом, тогда Мэдисон будет его есть.».
Символически эквивалентность записывается А ≡В («если и только если А, то В»).
Логическое значение эквивалентности соответствует таблице истинности:
-
А
В
А≡В
И
И
И
И
Л
Л
Л
И
Л
Л
Л
И
Эквивалентное суждение со связанными по содержанию членами выражает одновременно условие достаточное и необходимое: (А→ В) ≡(В→ А).
Равносильность выражений (А«В) и (А→ В) ≡ (В→А) может быть доказана с помощью таблицы истинности.
Отрицание – это логическая операция, с помощью которой из одного высказывания получают новое, при этом простое суждение Pпревращается в сложное, и если исходное простое суждение истинно, то новое сложное суждение ложно – «неверно, что P» или «высказывание А ложно тогда, когда высказывание А¯ истинно»
-
А
А¯
И
Л
Л
И
Двойное отрицание – это операция по отрицанию отрицательного суждения. Повторное отрицание ведет к утверждению или, иначе, отрицание отрицания равносильно утверждению: А→ А˭– «если А, то неверно, что не-А», или А˭ºА – «неверно, что не-А, если и только если верно, что А».
-
А
А¯
И
И
Л
Л
4. Приведите четыре содержательных примера простого категорического силлогизма (по одному примеру для каждой фигуры; модусы любые). Для каждого примера дайте его логический анализ: укажите модус, термины, распределенность терминов, большую и меньшую посылки (их вид), обоснуйте правильность вывода, используя ссылки на известные правила простого категорического силлогизма.
Простой категорический силлогизм — рассуждение, состоящее из трёх простых атрибутивных высказываний: двух посылок и одного заключения. Посылки силлогизма разделяются на бо́льшую (которая содержит предикат заключения) и меньшую (которая содержит субъект заключения). По положению среднего термина силлогизмы делятся на фигуры, а последние по логической форме посылок и заключения — на модусы.
В силлогизм входит ровно три термина:
S — меньший термин: субъект заключения (входит также в меньшую посылку);
P — больший термин: предикат заключения (входит также в большую посылку);
M — средний термин: входит в обе посылки, но не входит в заключение.
Фигуры силлогизма - это его разновидности, различающиеся положением среднего термина (М) в посылках.
Посылки изображаются горизонтальными отрезками, крайние точки отрезков обозначают термины, а наклонные или вертикальные линии соединяют средний термин в разных посылках)
Возможны 4 варианта таких структур:
I фигура
В 1-й фигуре средний термин занимает место субъекта в большей посылке предиката в меньшей.
Пример:
Все мыши (М) любят грызть сыр (Р)
Маус (S) - мышь (М)
Маус (S) любит грызть кость (Р)
Правила 1-й фигуры:
1) бoльшая посылка должна быть общей (А или Е);
2) мeньшая посылка должна быть утвердительной (А или I).
II фигура
Во 2-й фигуре средний термин занимает место предиката в обеих посылках
Пример:
“Некоторые юристы (M-) – члены коллегии адвокатов (P)”, “Все сотрудники нашего института (S) – юристы (М-)”
Правила 2-й фигуры:
1) бoльшая посылка должна быть общим суждением (А, Е);
2) одна из посылок должна быть отрицательным суждением (E, I).
III фигура
В 3-ей фигуре средний термин занимает место субъекта в обеих посылках.
Пример:
Ни один пингвин (M) не летает (P);
Все пингвины (M) птицы (S):
Некоторые птицы (S) не летают (P).
Правила 3-й фигуры:
1) мeньшая посылка должна быть утвердительным суждением (А, I);
2) заключение должно быть частным суждением (I, О).
IV фигура
В 4-й фигуре средний термин занимает место предиката в большей и субъекта в меньшей посылке.
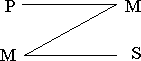
Пример:
Все акулы (P)- хищники (M);
Все хищники (M) догоняют своих жертв (S):
Некоторые рыбы, догоняющие своих жертв (S), есть акулы (P).