8. Реактор полного идеального смешения (рпс) и его характеристическое уравнение

Реактор полного смещения (рис. 8.1) является непрерывно действующим.

Рис. 8.1. Схема реактора полного смешения.

Условием идеальности в РПС является отсутствие градиента концентрации и температуры по объёму:

(dC_i/dV) = (dТ/dV) = 0;

Причем, в стационарных условиях этот градиент отсутствует и во времени:

(dC_i/dr) = 0;

При введении исходной смеси в большой реакционный объём происходит скачкообразное снижение концентраций до величины равной концентрации в реакторе.

Это проиллюстрировано на рис. 8.2:

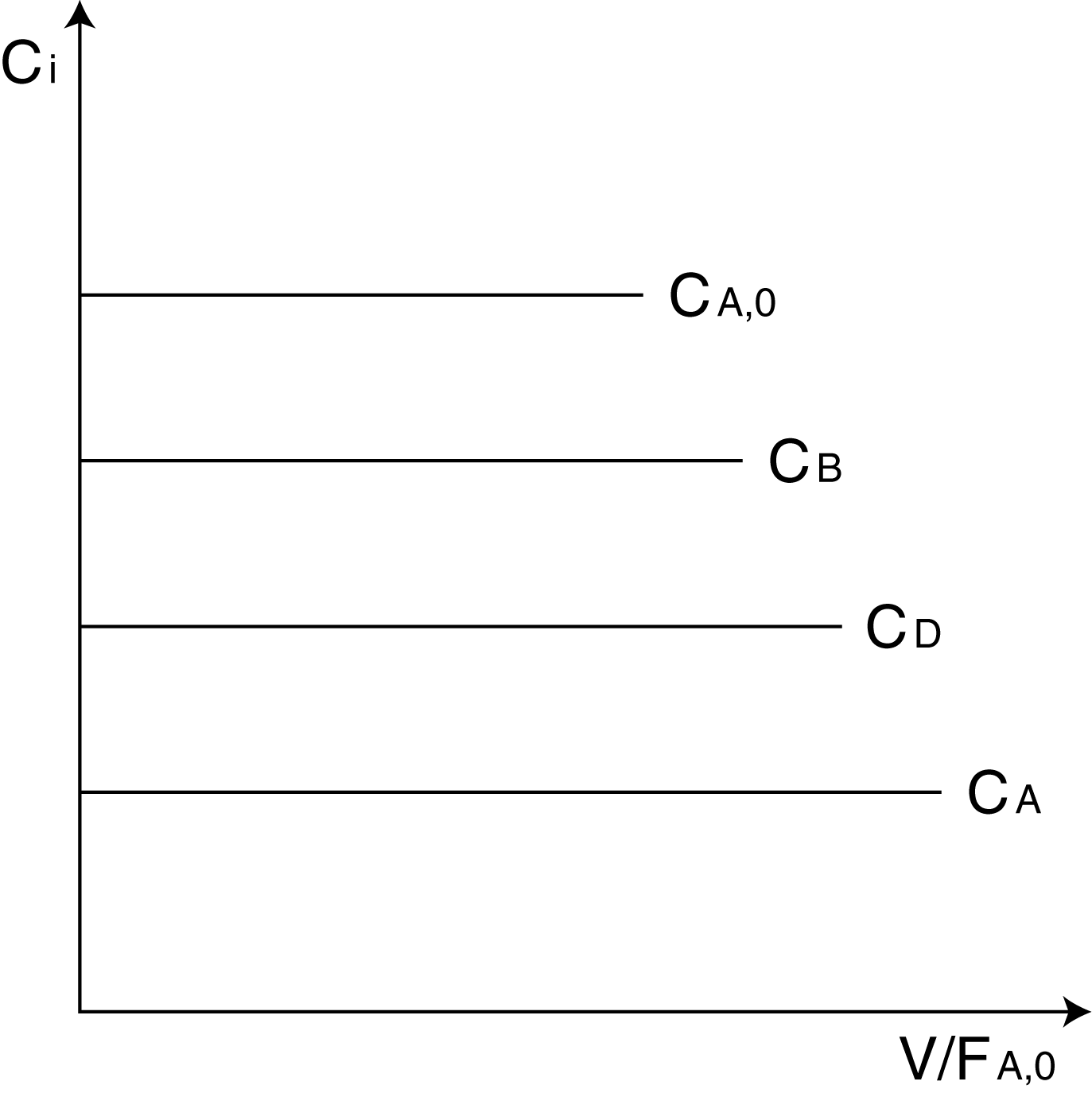
Рис. 8.2. Концентрационные кривые реактора полного смещения.

C_В, С_D – во времени не меняется.

Для стационарных условий работы можно составить уравнение материального баланса для РПС:

F_i – F_i,0 = r_i V (r_i m_К);

Из этого уравнения получаем характеристическое уравнение РПС:

Для гомогенных условий:

; (8-1)

Для гетерогенно-каталитических условий:

; (8-2)

При постоянстве объёмного потока W = const разделим (8-1) и (8-2) на W₀ и получим:

; (8-3)

; (8-4)

В уравнениях (8-3) и (8-4) С_i получается в соответствии с уравнением (3-1).

Чаще всего используют уравнения, выраженные через выходы и применимые не только при W = const, но и при переменном объёме смеси.

[(V/F_А,0) или (m_k/F_А,0)] = [('_i/'_A)  (x_i^A/r_i)]; (8-5)

В уравнениях (8-2) – (8-5) величина (V/W₀) или (m_k/W₀) [(V/F_i,0) или (m_k/ F_i,0)] имеют тот же смысл и наименование, что и для реакторов идеального вытеснения.

Уравнение (8-5) получено комбинацией (8-2) и (2-6).

В реакторах периодического действия и идеального вытеснения концентрация веществ изменяется во времени или по объёму и конечный результат находят после интегрирования, поэтому эти реакторы называются интегральными реакторами. В отличии от этого в РПС градиент концентрации отсутствует во времени и конечный результат находят решая алгебраические уравнения (8-2) – (8-5), что значительно упрощает расчёт. Реакторы РПС называют безградиентными реакторами. Безградиентные реакторы применяют для кинетических исследований, главным образом газофазных, в том числе, гетерогенно-каталитических реакций. Реактор может быть устроен по типу изображённому на рис. 8.3

Рис. 8.3. Схема проточно-циркуляционной установки с внешней циркуляцией.

Эти реакторы называют проточно-рециркуляционными. В них осуществляется циркуляция реакционной смеси через циркуляционное пространство. При высокой степени циркуляции (не менее 1:100), такие установки близки к модели РПС.

Остальное оснащение безградиентных реакторов и последовательность проведения опытов, такие же как в РИВ. Очень важно, что температурный режим в этих реакторах регулируется проще и точнее, а результаты исследований газофазных гетерогенно-каталитических реакций в безградиентных условиях считаются самыми достоверными.

9. Гипотеза о схеме превращений и способы её подтверждения

При изучении сложных реакций требуется выдвинуть гипотезу о схеме превращения т.е. о совокупности простых реакций протекающих в данной системе. Во многих случаях схему превращения можно составить, учитывая общие сведения по органической химии.

9.1. Способ изолирования отдельных реакций. Он состоит в изучении продуктов превращения компонентов смеси в условиях реакции в отсутствии других веществ или присутствии некоторых из них.

Пример:

В результате реакций этанола с аммиаком образуется смесь следующих продуктов: моно-, ди- и триэтаноламины, диэтиловый эфир, этилен, вода.

Из литературных данных известны следующие простые реакции образования этих продуктов:

2C₂H₅OH (C₂H₅)₂O + H₂O

C₂H₅OH C₂H₄ + H₂O

(C₂H₅)₂O C₂H₄ + C₂H₅OH

Можно предположить, что алкилирующим агентом является диэтиловый эфир. Для этого проводят реакцию аммиака с диэтиловым эфиром. При этом также получают смесь трех аминов, что позволяет дополнить схему превращения следующими тремя реакциями

Проверим поведение эфиров в условиях процесса алкилирования. Изолированное их превращение показало, что моно- и диэтиламин дают два продукта диспропорционирования, а из смеси триэтиламина с аммиаком получается моно- и диэтиламин. Кроме этого каждый амин распадается с образованием этилена. Учитывая обратимость реакций диспропорционирования аминов и необратимость их распада с образованием этилена, дополнительно имеем следующие превращения:

2C₂H₅NH₂ NH₃ + (C₂H₅)₂NH

C₂H₅NH₂ C₂H₄ + NH₃

2(C₂H₅)₂NH C₂H₅NH₂ + (C₂H₅)₃N

(C₂H₅)₂NH C₂H₄ + C₂H₅NH₂

NH₃ + (C₂H₅)₃N C₂H₅NH₂ + (C₂H₅)₂NH

(C₂H₅)₃N C₂H₄ + (C₂H₅)₂NH

Таким образом, полная схема превращений оказалась состоящей из 20 простых реакций, из которых только 5 стехиометрически независимы.

9.2. Кинетический метод. Для установления схемы превращения органических продуктов используют кинетический метод.

Пример:

Для подтверждения схемы:

Можно провести реакцию без добавления или с добавлением в исходную смесь предполагаемого промежуточного вещества P. При правильности гипотезы скорость образования продукта В при этом должна увеличиваться, а для продукта D должна оставаться неизменной. Для установления схем превращений иногда используется способ предварительного анализа экспериментально найденных кинетических кривых. Так при параллельном образовании веществ B и D по двум различным схемам: экстраполируют отношение скоростей (r_B/r_D) к нулевому времени реакции.

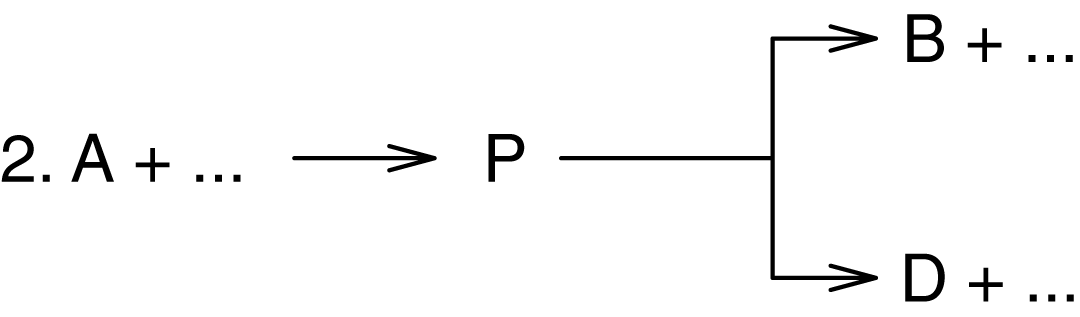
Если эти реакции идут по принятой гипотезе, то отношение (r_B/r_D) должно быть положительной величиной отличной от нуля и от бесконечности.

При последовательном превращении веществ:

в начальный момент времени скорости образования веществ B и D=0, поэтому соотношение (r_B/r_P) экстраполированное к нулевому времени должно быть равно нулю. Это должно быть справедливо и для соотношения (r_D/r_B). Таким образом, дифференцируя кинетические кривые находят производные dC_i/dt или dx_i/d(V/F_A,0) и их соотношения. Экстраполируя последнее к t₀ или V/F_A,0 = 0 можно установить параллельные или последовательные схемы превращения. Очевидно, и соотношение:

Поэтому то же самое можно сделать по кривым С_В – С_i или x_B – x_i построенным на основании экспериментальных данных.

Пример:

Из реагента А образуются продукты P, B и D. По кинетическим кривым, приведенным на рис. 9.1, составить вероятную схему превращений.

Рис. 9.1. Установление схемы превращений по кинематическим кривым для сложных реакций.

На основе рис. 9.1 строим следующий график (рис 9.2). Дифференцируем каждый из реагентов по времени.

Рис. 9.2. Установление схемы превращений по кривым соотношения скоростей для сложных реакций.

По виду кривых можно полагать, что вещество Р является промежуточным. Вещество В образуется параллельно с веществом Р, а вещество D последовательно из вещества P.

При экстраполяции t = 0 убеждаемся, что (r_D/r_P)  0 и (r_D/r_B)  0, а (r_B/r_P) отсекает на оси координат отрезок, не равный нулю. Отсюда следует вероятность такой схемы реакции:

Однако экспериментальные данные не исключают возможность частичного превращения: