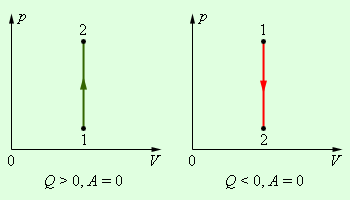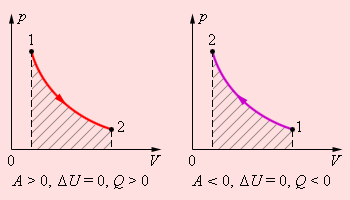13. МА́КСВЕЛЛА РАСПРЕДЕЛЕ́НИЕ, распределение по скоростям частиц (молекул) макроскопической физической системы, находящейся в состоянии термодинамического равновесия, (в отсутствии внешнего поля, при условии, что движение частиц подчиняется законам классической механики. Установлено Дж. К. Максвеллом в 1859. Закон Максвелла о распределении молекул идеального газа по скоростям основан на предположениях, что газ состоит из большого числа N одинаковых молекул, его температура постоянна, а молекулы совершают тепловое хаотическое движение. При этом на газ не действуют силовые поля. Функция распределения молекул по скоростям f(v)=dN(v)/Ndv определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dvи имеет смысл плотности вероятности. Для газа, подчиняющегося классической механике, в состоянии статистического равновесия функция распределения f Максвелла по скоростям имеет вид: f(v) =n(m/2kT)3/2exp(-mv2/2kT), Где m — масса молекулы, Т — абсолютная температура системы, k — постоянная Больцмана. Значение функции распределения f(v) зависит от рода газа (от массы молекул) и от температуры. С помощью распределения Максвелла можно вычислять средние значения скоростей молекул и любых функций этих скоростей. В частности, средняя квадратичная скоростьv2 = 3kT/m, а средняя скорость молекулы v = (8kT/m)1/2. Распределение Максвелла не зависит от взаимодействия между молекулами и справедливо не только для газов, но и для жидкостей, если для них возможно применить классическое описание. Распределение Максвелла вытекает из Гиббса распределения канонического в том случае, когда поступательное движение частиц можно рассматривать в классическом приближении, учитывая, что распределение по скоростям не зависит от распределения по пространственным координатам. Распределение Максвелла является частным решением кинетического уравнения Больцмана для случая статистического равновесия в отсутствии внешних полей. Распределение Максвелла не зависит от характера взаимодействия частиц системы и от внешних сил и потому справедливо как для молекул газа, так и для молекул жидкостей и твердых тел. Распределение Максвелла справедливо также для случая броуновского движения частиц, взвешенных в газе или жидкости.

14. Барометрическая формула и распределение больцмана

Барометрическая формула. Если температура не зависит от высоты, то давление газа меняется с высотой по закону: , где  — высота,  — молярная газовая постоянная,  — постоянная Больцмана,  — ускорение свободного падения вблизи поверхности земли,  — молярная масса газа,  — масса одной молекулы,  — абсолютная температура.

Поделив барометрическую формулу на  , с учетом уравнения состояния идеального газа, получим распределение Больцмана — зависимость концентрации молекул от потенциальной энергии: , где    — потенциальная энергия молекулы. В однородном поле силы тяжести  .

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру   и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения  одинаково), барометрическая формула имеет следующий вид:

где   — давление газа в слое, расположенном на высоте  ,   — давление на нулевом уровне ( ),   — молярная масса газа,   — газовая постоянная,   —абсолютная температура. Из барометрической формулы следует, что концентрация молекул   (или плотность газа) убывает с высотой по тому же закону:

где   — масса молекулы газа,   — постоянная Больцмана.

Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см.Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 году применил барометрическую формулу к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.

Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина  , определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной  . Чем выше температура  , тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести   (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести   может изменяться за счёт двух величин: ускорения  и массы частиц  .

Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.

Барометрическая формула лежит в основе барометрического нивелирования — метода определения разности высот   между двумя точками по измеряемому в этих точках давлению (  и  ). Поскольку атмосферное давление зависит от погоды, интервал времени между измерениями должен быть возможно меньшим, а пункты измерения располагаться не слишком далеко друг от друга. Барометрическая формула записывается в этом случае в виде:   (в м), где   — средняя температура слоя воздуха между точками измерения,   — температурный коэффициент объёмного расширения воздуха. Погрешность при расчётах по этой формуле не превышает 0,1—0,5 % от измеряемой высоты. Более точна формула Лапласа, учитывающая влияние влажности воздуха и изменение ускорения свободного падения.

15. Число степеней свободы

Одной из основных характеристик термодинамической системы является ее внутренняя энергия U — энергия хаотического (теплового) движения микрочастиц системы (атомов, молекул, ядер, электронов и т. д.) и энергия взаимодействия этих частиц. Из этого определения следует, что к внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.  Внутренняя энергия — определенная функция термодинамического состояния системы, т. е. в любом состоянии система обладает вполне определенной внутренней энергией (она не зависит от того, каким образом система пришла в данное состояние). Это значит, что при переходе системы из одного состояния в другое изменение внутренней энергии задается только разностью значений внутренней энергии данных состояний и не зависит от пути и способа перехода.  В механике введилось понятие числа степеней свободы: это число независимых переменных (координат), которые полностью определяют положение системы в пространстве. В некоторых задачах молекулу одноатомного газа (рис. 1, а) рассматривают как материальную точку, которой задают три степени свободы поступательного движения. При этом не учитывается энергия вращательного движения.  В механике молекула двухатомного газа в первом приближении считается совокупностью двух материальных точек, которые жестко связанны недеформируемой связью (рис. 1, б). Данная система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла. Значит, у двухатомного газа пять степеней свободы (i = 5). У трехатомной (рис. 1, в) и многоатомной нелинейной молекулы шесть степеней свободы: три поступательных и три вращательных. Естественно считать, что жесткой связи между атомами не существует. Поэтому необходимо учитывать для реальных молекул также степени свободы колебательного движения. 

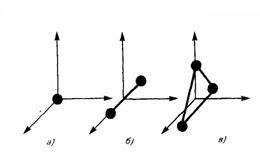
Рис.1

При любом числе степеней свободы данной молекулы три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, значит на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε₀> (энергия поступательного движения молекул):    В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы    где i — сумма числа поступательных, числа вращательных в удвоенного числа колеба¬тельных степеней свободы молекулы:i=i_пост+i_вращ+2i_колеб  В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.  Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий N_A молекул:   (1)  Внутренняя энергия для произвольной массы m газа.    где М — молярная масса, ν — количество вещества. 

Первое начало термодинамики

В термодинамике широко используются понятия молярной теплоемкости при постоянном объеме C_V и молярной теплоемкости при постоянном давлении C_p. В идеальном газе они удовлетворяют уравнению Майера: 

Cp – CV = R.

Теплоемкость одного моля одноатомного идеального газа при постоянном объеме равна   , двухатомного –   , многоатомного – 3R.

Внутренняя энергия идеального газа прямо пропорциональна его абсолютной температуре: 

U = CVT.

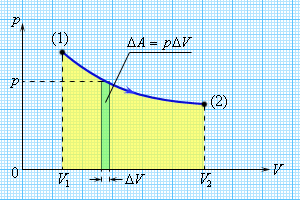
Работа ΔA, совершаемая газом, определяется давлением газа и изменением его объема: 

ΔA = pΔV.

Рисунок 2.3.1. Если давление газа в процессе совершения работы изменяется, то работа может быть найдена по площади под графиком.

Рисунок 2.3.2. Работа газа зависит от пути, по которому газ переходит из состояния 1 в состояние 2.

 

Первое начало термодинамики. Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и на совершение работы над внешними телами: 

Q = ΔU + A.

В изохорном процессе газ работы не совершает, и ΔU = Q. В изобарном процессе A = pΔV = p (V₂ – V₁). В изотермическом процессе ΔU = 0, и A = Q; вся теплота, переданная телу, идет на работу над внешними телами. Графически работа равна площади под кривой процесса на плоскости p, V.

Рисунок 2.3.3. Первое начало термодинамики для изохорного процесса.

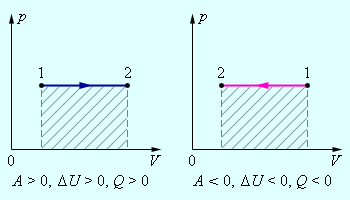
Рисунок 2.3.4. Первое начало термодинамики для изобарного процесса.

Рисунок 2.3.5. Первое начало термодинамики для изотермического процесса.

Рисунок 2.3.6. Первое начало термодинамики для адиабатного процесса.

Адиабатным называется квазистатический процесс, при котором системе не передается тепло из окружающей среды: Q = 0. В адиабатном процессе вся работа совершается за счет внутренней энергии газа.

Первое начало термодинамики :

Количество теплоты, сообщенное телу, идет на увеличение его внутренней энергии и на совершение телом работы над внешними телами:

dQ = dU + dA

или

Изменение внутренней энергии тела равно разности сообщенного телу количества теплоты и произведенной над ним механической работы:

dU = dQ - dA