. Уравнение Шредингера для стационарных состояний

Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)

где l — ширина «ямы», а энергия отсчитывается от ее дна (рис. 296).

Уравнение Шредингера (217.5) для стационарных состояний в случае одномерной задачи запишется в виде

                                        (220.1)

По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х=0 и х=1) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные усло­вия в данном случае имеют вид

                                                         (220.2)

В пределах «ямы» (0  х  l) уравнение Шредингера (220.1) сведется к уравнению

или

                                                   (220.3)

где

                                                        (220.4)

Общее решение дифференциального уравнения (220.3):

Так как по (220.2) (0)=0, то В=0. Тогда

                                                     (220.5)

Условие (220.2) (l)=A sin kl = 0 выполняется только при kl = n, где n — целые числа, т. е. необходимо, чтобы

                                                       (220.6)

Из выражений (220.4) и (220.6) следует, что

                                               (220.7)

т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е_n, зависящих от целого числа п. Следовательно, энергия Е_n частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е_n называются уровнями энергии, а число п,определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Е_n, или, как говорят, частица находится в квантовом состоянии n.

Подставив в (220.5) значение k из (220.6), найдем собственные функции:

Постоянную интегрирования А найдем из условия нормировки (216.3), которое для данного случая запишется в виде

В результате интегрирования получим А = , а собственные функции будут иметь вид

                                                          (220.8)

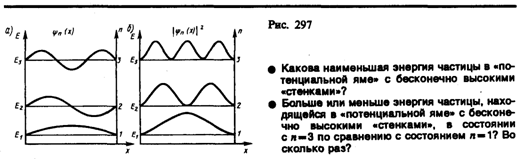
Графики собственных функций (220.8), соответствующие уровням энергии (220.7) при n = 1, 2, 3, приведены на рис. 297,а. На рис. 297,6 изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная |_n(х)|² = _n(х)*_n(х) для n=1,2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n=2 частица не может находиться в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.

Из выражения (220.7) вытекает, что энергетический интервал между двумя сосед­ними уровнями равен

                                               (220.9)

Например, для электрона при размерах ямы l=10^–1 м (свободные электроны в метал­ле) E_n  10^–35n Дж  10^–16n эВ, т. е. энергетические уровни расположены столь тесно, что спектр практически можно считать непрерывным. Если же размеры ямы соизмеримы с атомными (l10^–10 м), то для электрона E_n  10^–17n Дж 10²n эВ, т. е. получаются явно дискретные значения энергии (линейчатый спектр). Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не накладывает.

Кроме того, квантово-механическое рассмотрение данной задачи приводит к выводу, что частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная  . Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты х частицы в «яме» шириной l рав­на x=l. Тогда, согласно соотношению неопределенностей (215.1), импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса ph/l. Такому разбросу значений импульса соответствует кинетическая энергия E_min(p)²/(2m) = h²/(2ml²). Все остальные уровни (n>1) имеют энергию, превыша­ющую это минимальное значение.

Из формул (220.9) и (220.7) следует, что при больших квантовых числах (n>>1) E_n/E_n2/n<<1, т. е. соседние уровни расположены тесно: тем теснее, чем больше n. Если n очень велико, то можно говорить о практически непрерывной последователь­ности уровней и характерная особенность квантовых процессов — дискретность — сглаживается. Этот результат является частным случаем принципа соответствия Бора (1923), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.

Более общая трактовка принципа соответствия, имеющего огромную роль в современной физике, заключается в следующем: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применения, причем в определенных предельных случаях новая теория переходит в старую. Так, формулы кинематики и динамики специальной теории относительности переходят приv<<с в формулы механики Ньютона. Например, хотя гипотеза де Бройля приписывает волновые свойства всем телам, но в тех случаях, когда мы имеем дело с макроскопическими телами, их волновыми свойствами можно пренебречь, т. е. применять классическую механику Ньютона.

8. Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы  .

 Квантовый гармонический осциллятор

Конспект лекции (с демонстрациями)

Аннотация: изучение качественной стороны решения уравнения Шредингера для гармонического осциллятора, выяснение отличий получаемых результатов от выводов классической механики. (Традиционное изложение темы, дополненное демонстрациями на компьютерных моделях.)

Содержание

Одна из важных задач о движении микрочастиц – это задача о движении гармонического осциллятора - системе, способной совершать гармонические колебания. История квантовой теории реально начинается с Макса Планка, который в 1900 г. получил формулу для правильного описания спектрального распределения теплового излучения. Планк пришел к выводу, что не может обеспечить вывод своей магической формулы для распределения излучения, если только не сделать предположения, которое с философской точки зрения он считал почти неприемлемым. Это предположение заключалось в том, что рассматриваемые им в качестве излучателей гармонические осцилляторы должны обладать энергиями, не распределенными как непрерывные переменные (чего следовало бы ожидать), а принимающими дискретные и регулярным образом расположенные значения. Осцилляторы с частотой υ должны были обладать значениями энергии, которые были бы кратны, т.е. n раз умножены (где n = 0,1, 2,3,...) на нечто, названное им квантом энергии hυ.

Рассмотрим одномерный случай. (Трехмерные задачи сложны в математическом отношении, а практически все принципиальные особенности движения микрочастиц можно выявить и на одномерных задачах.) Изменение потенциальной энергии по оси x описывается формулой

Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?

• Колебания маятника с малой амплитудой.

• Другой пример – вертикальные колебания грузика, подвешенного на пружине.

В мире микрочастиц примерами могут быть колебания двухатомной молекулы или колебания атомов в кристаллах. Существенным для всех примеров является ограничение движения некоторой областью значений x. Частица не может покинуть параболическую потенциальную яму, края которой уходят на бесконечность.

Из классической механики известно, что проекция движения частицы на ось x представляет собой синусоидальное колебание около положения равновесия x = 0 с частотой:

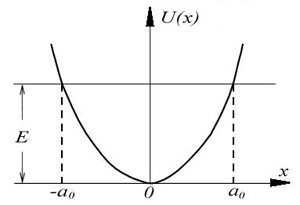
Точки a₀ и -a₀, в которых полная энергия частицы E равна потенциальной энергии, являются для частицы точками поворота. Плотность вероятности обнаружения колеблющейся частицы в различных точках оси x описывается формулой

Минимальна вероятность найти частицу около положения равновесия, где она движется с максимальной скоростью. Вблизи точек поворота частица как бы "зависает", и там вероятность обнаружения максимальна.

Оценка минимальной энергии осциллятора

Посмотрим, к каким выводам о характере движения приводит квантовая механика. Начнем с простой оценки минимального значения энергии осциллятора E. Полная энергия осциллятора E складывается из кинетической и потенциальной энергий:

Используя соотношение неопределенности Гейзенберга, в качестве оценки значения импульса p возьмем p ~ ћ/x.

Для малых значений x кинетическая энергия превышает потенциальную, тогда как при больших значениях x имеет место обратное соотношение между ними. Для основного состояния, где энергия минимальна, найдем минимум функции (2). Значение переменной x_min, соответствующее минимуму, равно:

а соответствующее значение энергии E имеет порядок

Заметим, что оценка энергии основного состояния дает ненулевое(!) значение. Уже простые вычисления приводят к нетривиальному результату.

Решения уравнения Шредингера

Нахождение точного решения требует решения уравнения Шредингера с потенциальной энергией (1), которое имеет вид

Трудности решения связаны со слагаемым, содержащим x². Приведем здесь только результаты вычислений. Анализ показывает, что, как и в случае с прямоугольной потенциальной ямой, волновые функции, являющиеся решением этого уравнения, будут непрерывными и конечными не при всех значениях энергии E, а лишь при дискретномнаборе значений:

где n принимает значения 0, 1, 2, ... . Отметим, что энергетические уровни гармонического осциллятора в отличие от случая прямоугольной потенциальной ямы расположены на одинаковом энергетическом расстоянии друг от друга ΔE = hυ.

Важной особенностью решения является наличие так называемых нулевых колебаний - колебаний с энергией, соответствующих значению квантового числа n = 0. Отличие от нуля минимальной энергии осциллятора характерно для всех квантовых систем и является следствием соотношения неопределенностей (см. оценку выше). В реальных квантовых системах, например, кристаллах, эти колебания сохраняются, как показывает опыт, даже при температурах, близких к абсолютному нулю, когда, казалось бы, все тепловое движение должно прекратиться. Опыты по рассеянию света кристаллами при низких температурах это подтверждают. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий (пример ниже) и других молекулярных явлений.

Первые три волновых функции гармонического осциллятора выглядят так:

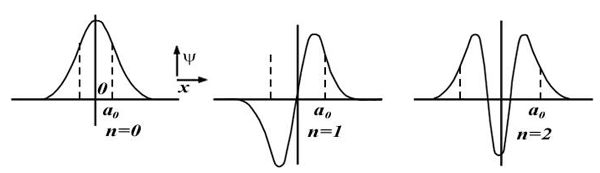
Здесь введено обозначение x₀² = h/(4π²mυ).

Графики этих волновых функций представлены на рисунке ниже.

Пунктиром показаны границы, между которыми совершала бы колебания классическая частица. Значения a₀ отличаются для разных n, так как от n зависит энергия Е  (~E^1/2). Очевидно, что при малых значениях квантового числа n плотность вероятности нахождения частицы, определяемая квадратом модуля волновой функции ψ₀(x)², кардинальным образом отличается от плотности вероятности обнаружения классического осциллятора: в основном состоянии максимальное значение вероятности приходится на центр, модуль волновой функции для всех квантовых чисел n имеет наибольшие значения между классическими точками поворота и экспоненциально убывающие "хвосты" вне этих точек.

Определим для основного состояния, как велика вероятность P обнаружения частицы вне пределов классической области, т.е. вне области -a₀ < x < a₀. Значение a₀ находится просто

Найдем сначала вероятность обнаружения частицы в классической области

где y = x/x₀. Поскольку под интегралом находится четная функция переменной y, то

Полученный интеграл называется интегралом вероятностей, значения его для различных значений верхнего предела имеются в таблицах. В нашем случае (интеграл от 0 до 1)P_кл ≈ 0.84. Соответственно, вероятность того, что частица будет обнаружена вне классической области, равна P = 1 - P_кл ≈ 0.16. Очень значительная величина!

.

       Из (5.3.4) вытекает, что энергия квантового осциллятора изменяется только порциями, т.е. квантуется. Причем, как и в прямоугольной яме, энергия ограничена снизу минимальным значением

       – энергия нулевых колебаний (прямое следствие соотношения неопределенностей). Это означает, что частица не может находиться на дне потенциальной ямы.

       Плотность вероятности нахождения частицы  изображена на рис. 5.2. Как и в случае прямоугольной потенциальной ямы, при n = 2 в середине ямы частица находиться не может. Это совершенно непонятно с классической точки зрения. Квантуется не только энергия, но и координата частицы.

Молекулярно-кинетическая теория (МКТ) устанавливает связи между макро- и микропараметрами идеального газа. Основное уравнение МКТ выражает выражает связь давления газа со средней кинетической энергией поступательного движения молекул. Давление газа на стенки сосуда является результатом многочисленных ударов молекул. При каждом ударе стенка получает силовой импульс, величина которого зависит от скорости молекул и, следовательно, от энергии их движения. При огромном числе ударов создается постоянное давление газа на стенку. Число ударов зависит от концентрации молекул n. Таким образом, можно ожидать, что давление газа связано с концентрацией молекул и с энергией их движения. Получим основное уравнение МКТ.

Рассмотрим сферический объём радиуса R, в котором находится N молекул идеального газа. Рассмотрим движение одной из них. Допустим, что молекула двигалась прямолинейно с импульсом  ударилась о стенку под углом ψ к нормали и отскочила от неё под тем же углом, имея импульс  . Найдём импульс, переданный молекулой стенке при ударе. Из закона сохранения импульса:

Т. к. удар упругий,   и  = 0, поэтому   направлен по нормали к стенке и по модулю равен:

.

Путь, который молекула проходит от одного удара о стенку до другого, равен хорде АВ, т. е. величине 2Rcosψ.

Найдем число ударов молекулы о стенку за одну секунду. Оно равно отношению скорости молекулы   к пути, проходимому молекулой от одного столкновения со стенкой до другого:

.

Сталкиваясь со стенками сосуда, одна молекула за одну секунду сообщает ей импульс

Суммарный импульс, сообщенный всеми N молекулами стенке сосуда за одну секунду будет равен

.

Из II закона Ньютона следует, что импульс, сообщённый за единицу времени стенке, численно равен силе, поэтому сила давления, действующая на поверхность сосуда, равна

.

Давление найдём, разделив силу на площадь поверхности сферического сосуда:

,

где   – объём сосуда с газом.

Перепишем полученное равенство в виде:

Помножив и поделив правую часть на число молекул N в объёме V, получим:

 или       (9)

Здесь введена величина   – средняя квадратичная скорость, равная корню квадратному из суммы квадратов всех скоростей, делённой на число молекул:

.              (10)

Тогда

,            (11) где n   –концентрация молекул.

Это уравнение называется основным уравнением молекулярно-кинетической теории идеального газа.

Получим связь давления со средней кинетической энергией поступательного движения молекулы

.              (12)

Из формулы (11)  , следовательно:

.            (13)

Таким образом, давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы. Это утверждение можно считать другой формулировкой основного уравнения молекулярно-кинетической теории идеального газа.
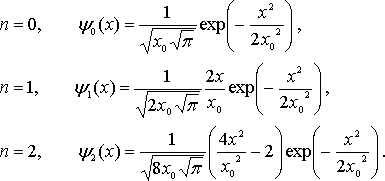