Зависимость рентабельности продукции у (%) от ее трудоемкости х (ч/ед.)

X	У	1 J = *	X У	JC2	А 1х	А Ух	А	Л У-Ух
1,0	32	0,0312	0,0312	1,00	0,0285	35,1	0,0027	-3,1
1,2	28	0,0357	0,0428	1,44	0,0341	29,3	0,0016	-1,3
1,5	22	0,0455	0,0682	2,25	0,0424	23,6	0,0031	-1,6
* 2,0	' 20	0,0500	0,1000	4,00	0,0563	17,7	-0,0063	2,3
2,5	16	0,0625	0,1563	6,25	0,0703	14,2	—0,0078	1,8
2,7	15	0,0667	0,1800	7,29	0,0758	13,2	-0,0091	1,8
3,0	10	0,1000	0,3000	9,00	0,0842	11,9	0,0158	-1,9
13,9	143	0,3916	0,8785	31,23	0,3936	145,0	0,0000	-2,0

7

7

по МНК система нормальных уравнений примет вид:

У У

Исходя из данных табл. 2.6, имеем:

7д+13,9-А = 0,3916, 13,9-Д+31,23^ = 0,8785.

Решая эту систему уравнений, получим оценки параметров искомой функции: а — 0,0007; b = 0,0278. Соответственно уравне­ние регрессии составит:

1

Ух =

0,0007+0,0278-jc

Сравним последние две графы табл. 2.6. Получим Т,(у-УхУ* 0> ^тогД^а как для обратных значений эта величина равна

г

нулю. Кроме того, заметим, что положительные отклонения фак­тических и теоретических обратных значений сменяются на отрицательные значения для аналогичных показателей по исход­ным данным. Уравнение отражает обратную связь рассматривае­мых признаков: чем выше трудоемкость, тем ниже рентабель­ность. Поскольку данное уравнение линейно относительно

величин —, то если обратные значения — имеют экономический

Для оценки параметров исследуемой функции у = '

a+b-дс+s

У У

смысл, коэффициент регрессии b интерпретируется, так же как в линейном уравнении регрессии. Если, например, под у подразу­меваются затраты на 1 руб. продукции, а под х — производитель­ность труда (выработка продукции на одного работника), то об­ратная величина характеризует "затратоотдачу и параметр b имеет экономическое содержание — средний прирост продукции в сто­имостном измерении на 1 руб. затрат с ростом производитель­ности труда на единицу своего измерения.

78

мость результативного признака от фактора. Оно целесообразно при очень медленном повышении уровней результативного Признака с ростом значений фактора.

Возможно и одновременное использование логарифмирова­ния, и преобразование в обратные величины: у = е^а " ^{ь/х +} ** Про-

I

логарифмировав, получим: Iny = а — Ь / х + е. Далее заменим —

Ь х

на z, и тогда для оценки параметров к линейному уравнению

1пу = д — А-г + е может быть применен МНК.

При всех положительных значениях х функция возрастает, при х = Ь/2 кривая имеет точку перегиба — ускоренный рост при х < Ь/2 сменяется на замедленный рост при х > Ь/2. Подобного типа функции используются при анализе статистических данных о бюджетах потребителей, где выдвигается гипотеза о существо­вании асимптотического уровня расходов, об изменении пре­дельной склонности к потреблению товара, о существовании «порогового уровня дохода»¹. В этом случае при х оо у # (рис. 2.5).

Рис. 2.5. Функция насыщения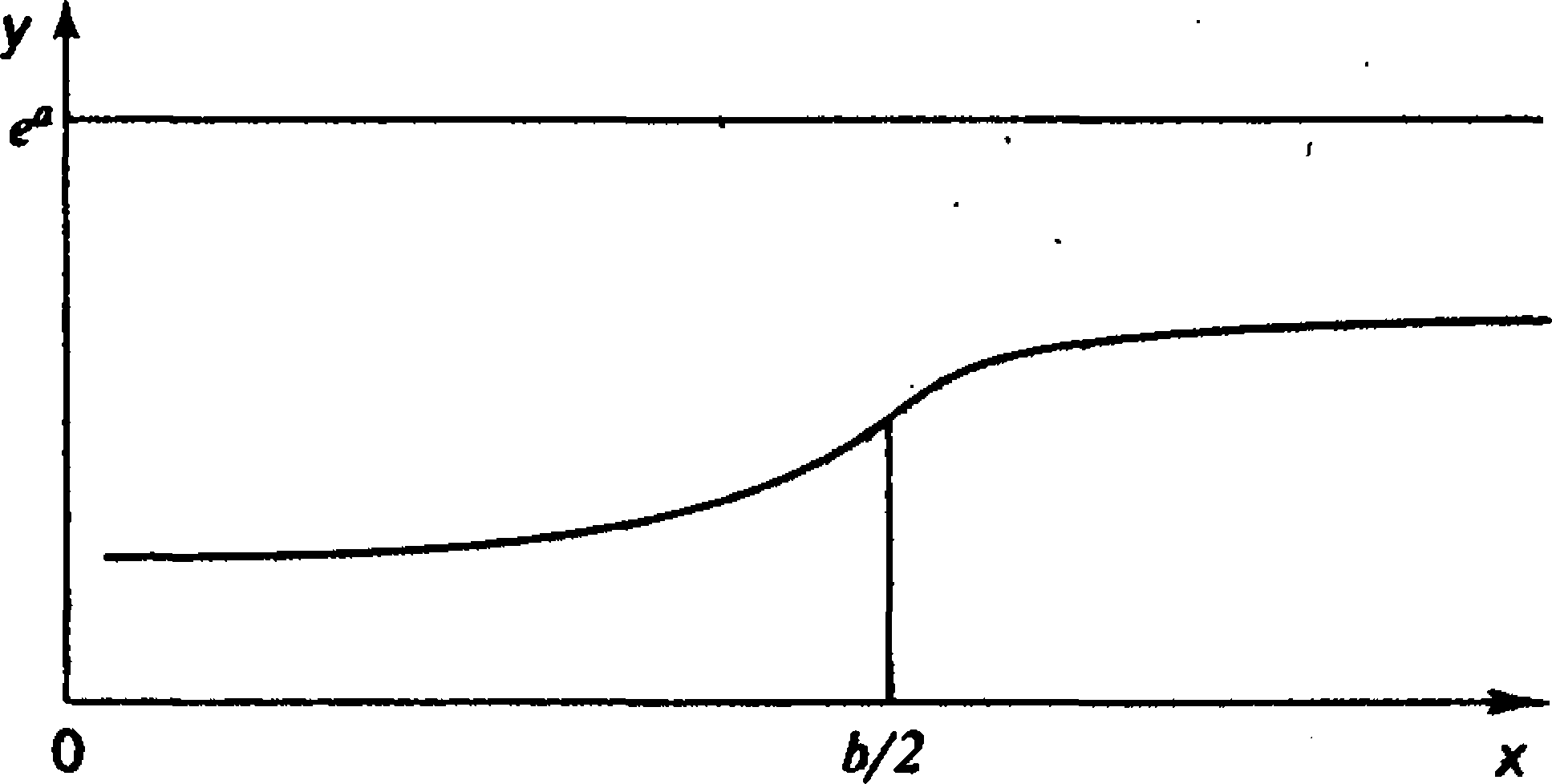

При использовании линеаризуемых функций, затрагиваю­щих преобразования зависимой переменной у, следует особенно проверять наличие предпосылок МНК (они будут рассмотрены в п. 3, 10), чтобы они не нарушались при преобразовании. При не-