2.2 Основы теории деревьев

Теория деревьев основана на теории графов, так как дерево – это связанные цикличные не ориентированные графы.

Дерево не имеет петель и кратных ребер. Любые две вершины дерева связанны между собой единственной простой цепью. При добавлении любого ребра к дереву образуется один цикл. При удалении одного ребра, разрушается связность, и дерево распадается на компоненты. В связи с этим дерево можно также определить как минимальный связный граф. Минимальность понимается в том смысле, что он не содержит подграфа, состоящего из всех его вершин и являющегося связным. Достаточное условие для того, чтобы граф назывался деревом – единственная цепь между двумя вершинами, (рис 1.3)

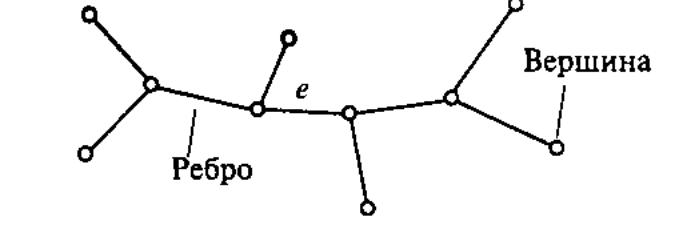рис 1.5

Лесом – называется граф,компаненты которого являются деревьями.

Ориентированное дерево – это дерево, в котором никакие две дуги не заходят в одну и ту же вершну,это ориентированный граф без циклов, в котором полустепень захода вершины равна 1.

Для оценки степени сложности дерева используются следующие характеристики:

• Порядок узла – число его дочерних узлов

• Порядок дерева – наибольший порядок его узлов

• Глубина узла – число его предков плюс 1

• Глубина или высота дерева – наибольшая глубина его узлов

• Расстояние d(x,y) вершены х. и y в дереве – что число ребер в цепи, соединяющей эти вершины

• Эксцентриситет e (x) вершины x до наиболее удаленной от нее вершины

2.3 Основы теории сетей

Сетью – называется конечный граф N = (K;R) без циклов и петель, ориентированный в одном общем направлении от вершин x, являющихся входами графа, к вершинам y , являющимся его выходами.

Сети используются для моделирования способов пересылки в заданном направлении некоторых объектов из одной вершины графа в другую по его дугам. Поэтому в сетях чаще употребляют термин «связь» вместо терминов «ребро» или «дуга». Вместо термина «вершина» используют термин «узел». Узел служит для обозначения физического объекта.

В теории сетей используются следующие понятия:

• Источник s – узел, из которого начинается перемещение объектов; источник порождает поток, например предприятия сервиса, порождает поток потребительских товаров

• Строк t – узел, в которой заканчивается перемещение объектов; сток поглощает поток, например потребитель потребляет товары; все другие узлы называются промежуточными;

• Единицы потока – объекты, которые перемещаются или «протекают» из источника в сток.

Каждый нулевой столбец матрицы смежности соответствует источнику, а каждая нулевая строка – стоку.

В сети каждой дуге (связи) приписывается величина c (x;y)- пропускная способность, характеризующая максимальное число единиц потока, которая связь может пропустить. Такую связь часто называют транспортной. Сеть с заданными пропускным способностями её связей называют нагруженной сетью (рис 1.6). Если направление движения по дуге совпадает с ориентацией сети, дугу называют прямой, в противном случае её называют обратной. Связь сети называют насыщенной, если поток связей равен ее пропускной способности.

Циркуляцией – называется поток по связям сети, для которого в каждом узле выполняется условие сохранения.

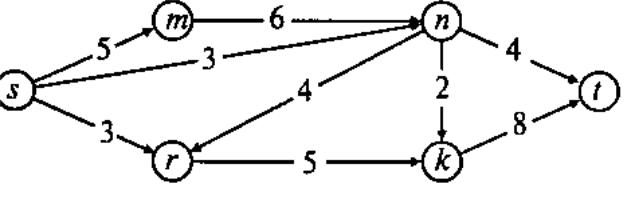рис 1.6