
- •Организация и задачи статистики в рб
- •Статистическое наблюдение
- •Сводка вторая стадия статистического исследования . Её понятие, организация и техника проведения
- •Задачи и виды стат. Группировок, выбор группировочных признаков, определение группировочных интервалов.
- •Абсолютные величины. Способы их получения и единицы измерения.
- •Относительные величины в статистике, виды относительных величин
- •Сущность и значение средних величин. Основные научные положения исчисления теории о средних величинах
- •Виды средних величин
- •Средняя арифметическая величина, её свойства и способы вычисления
- •Средняя гармоническая величина
- •Мода и медиана. Их использование в статистике
- •Медиана
- •Понятие вариации и признака, показатели вариации и признака и методы из расчёта
- •Дисперсия. Её математические свойства и способы расчёта.
- •Дисперсия альтернативного признака
- •Виды дисперсий, правило сложения дисперсий и его использование в анализе взаимосвязей между явлениями.
- •Понятие и принципы организации выборочного наблюдения
- •Способы и виды отбора единиц в выборочную совокупность
- •Ошибки выборочного наблюдения
- •Аналитические показатели рядов динамики
- •Средние показатели рядов динамики
- •Статистические методы выявления основной тенденции в развитии явлений. Понятие об интерполяции и экстраполяции.
- •Изучение сезонных колебаний
- •Понятие об индексах. Задачи, решаемые индексным методом. Виды индексов
- •Агрегатные форма свободных (общих) индексов
- •1) Агрегатные индексы объемных показателей.
- •2)Агрегатные индексы качественных показателей
- •Взаимосвязи индексов и выявление роля отдельных факторов в изменении сложного явления
- •Построение территориальных/ пространственных индексов
- •Виды и формы взаимосвязи, изучаемые в статистике. Задачи статистического измерения взаимосвязей.
- •Статистические методы изучения взаимосвязей между явлениями
- •Задачи, решаемые методом регресионно-корряляционного анализа (рка). Выбор формы связи и построение уравнения регрессии
- •Измерение тесноты корреляционной связи при криволинейных и прямолинейных зависимостях
Сущность и значение средних величин. Основные научные положения исчисления теории о средних величинах
Введём следующие понятия и обозначения.
Х – усредняемый признак, т.е. признак, по которому рассчитывается средняя величина.
Xi – Значения или варианты признака Х у отдельных единиц совокупности.
N – Число единиц совокупности
 – искомая величина.
– искомая величина.
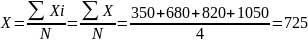
Под средней величиной понимается обобщающий показатель, характеризующий типичный уровень признака в расчёте на единицу однородной совокупности явлений.
Совокупность была весьма однородная.
Основные научные значения средних величин. Основными направлениями использования средних величин в экономическом анализе являются:
Характеристика уровня массовых общественных явлений.
Изучение тенденций развития явлений во времени.
Проведение сравнительного анализа.
Измерение взаимосвязи между явлениями.
Планирование и контроль хода экономических процессов.
Основными требования, применяемые к научному исчислению средних величин, являются
Их расчёт должен производиться по однородным, однокачественым явлениям
Правильный выбор единицы явления, на которую рассчитывается средняя величина
Расчёт и исчисление величина основе достоверных данных по всему кругу явлений или по типичной их части
При расчёте средних величин необходимо достижение сравнимости исходных данных.
Целесообразность использования не одного, а системы средних величин для характеристики массовых явлений.
Виды средних величин
В статистике наиболее часто встречаются и используются следующие 4 вида средних величин:
Среднее арифметическое
Среднее гармоническое
Среднее квадратическое
Среднее геометрическое
Из указанных средних чаще всего применяется среде арифметическое, реже – среднее гармоническое. Среднее квадратическое используется при исчислении показателей вариации и в тех случаях, когда приходятся усреднять величины, входящие в исходную информацию в виде квадратных функций. Среднее геометрическое – при расчёте средних темпов динамики
Для определения конкретного вида средней величины в статистике имеется критерий в виде определяющего свойства средней, т.е. выбор правильного вида средней зависит от механизма формирования общего объёма изучаемого признака. Если общие объём признака образуется как сумма отдельных вариант, то применяется среднее арифметическое, если как сумма обратных значений вариант, то применяется среднее гармоническое, если как сумма квадратов значений вариант, то среднее квадратическое, если как произведение отдельных вариант – то среднее геометрическое.
Все средние величины в зависимости от характера исходных данных подразделяются на простые и взвешенные. Основой для вычисления простых средних служат индивидуальные значения признака по каждой единице совокупности. Основой для вычисления взевешенных средних служат группированные данные по исследованию данного признака.
Средняя арифметическая величина, её свойства и способы вычисления
Средняя
арифметическая простая
величина определяется по формуле
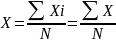 .
Средняя
арифметическая взвешенная
величина определяется по формуле
.
Средняя
арифметическая взвешенная
величина определяется по формуле
 , Fi
– частота повторение признака Xi
у различных единиц совокупности.
Рассмотрим свойство средней арифметической.
Для уяснения сущности и упрощения
расчётов средней арифметической величины
используются следующие основные
свойства.
, Fi
– частота повторение признака Xi
у различных единиц совокупности.
Рассмотрим свойство средней арифметической.
Для уяснения сущности и упрощения
расчётов средней арифметической величины
используются следующие основные
свойства.
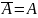 Среднее от постоянной
равно ей самой
Среднее от постоянной
равно ей самой
 Увеличение или
уменьшение одно и того же величну
приводит к изменению средней на ту же
величину.
Увеличение или
уменьшение одно и того же величну
приводит к изменению средней на ту же
величину.
 Умножение/деление
каждого варианта в А раз изменяет среднюю
во столько же раз.
Умножение/деление
каждого варианта в А раз изменяет среднюю
во столько же раз.
 Изменение каждого
из весов в одно и тоже количество раз
не изменяет величины среднего показателя.
Изменение каждого
из весов в одно и тоже количество раз
не изменяет величины среднего показателя.
Алгебраическая сумма отклонений всех вариантов от средней арифметической равно 0
 Среднее
от суммы или разности нескольких величин
равна сумме средних значений этих
величин.
Среднее
от суммы или разности нескольких величин
равна сумме средних значений этих
величин.
 0 Сумма квадратов
отклонений от средней арифметической
меньше, чем от любой другой величины.
0 Сумма квадратов
отклонений от средней арифметической
меньше, чем от любой другой величины.
При наличии всех индивидуальных или сгруппированных значений признака X, полученных в результате статистического наблюдения применяют формулу простой средней или взвешенной средней.(см. пfр. 1, 2)
При определении средней арифметической в интервальном ряду распределения осуществляется в 2 этапа:
Рассчитывается середина каждого интервала, которая принимается за новое значение Х, при этом для открытых интервалов их ширина условно принимается равной ширине соседних или смежных интервалов
Рассчитывается средняя арифметическая величина по формуле взвешенной средней
Для упрощения расчёта средней арифметической в интервальной ряду распределения с равными интервалами используется способ «моментов». Его суть основана на использовании свойств средней арифметической. Из всех вариантов Xi вычитается постоянная А, за которое принимается середина центрального интервала, или интервала, обладающего наибольшей частотой.
Полученные
разности деляться на ширину интервала
H,
в результате которого выделяется новая
переменная X’i.В
качестве весов используются значения
частот, выраженные в долях или процентах
от общего объёма совокупности.
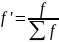 .
Далее рассчитывается среднее значение
для преобразованных вариантов X’.
.
Далее рассчитывается среднее значение
для преобразованных вариантов X’.
 .
Далее рассчитывается средняя величина
среднего признака. В тех случаях, когда
известно суммарное значение признака
Х по всей совокупности и общее количество
единиц изучаемой совокупности, то расчёт
средней арифметической величины, расчет
Х
.
Далее рассчитывается средняя величина
среднего признака. В тех случаях, когда
известно суммарное значение признака
Х по всей совокупности и общее количество
единиц изучаемой совокупности, то расчёт
средней арифметической величины, расчет
Х -
осуществляется по формуле агрегатной
средней
-
осуществляется по формуле агрегатной
средней
