Задачи, решаемые методом регресионно-корряляционного анализа (рка). Выбор формы связи и построение уравнения регрессии
Сущность
регрессионно-корреляционного анализа
заключается в построении и анализе
экономико-математической модели, которая
выражает зависимость результативного
признака от определяющих его факторных
признаков, в виде уравнения регрессии.
В общем виде эта зависимость: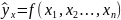
,
у – результативный признак, х – факторный
признак
Основные задачи, решаемые в процессе РКА:
1. Определение теоретической формы связи и расчёт параметров уравнения регрессии.
2. Измерение тесноты связи между результативным и факторным признаками
Выбор
формы связи между признаками осущ-ся
на основе теор. Анализа сущности явления
и характера исходных данных. При этом
для построения однофакторных моделей
м.б. выдвинута гипотеза о наличии
взаимосвязи в виде прямой линии:
,
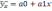уравнения параболы:
, гиперболы и т.д.
Для
нахождения параметров каждого из
уравнений используется метод наименьших
квадратов, а именно
,
-
факт-ое знач. результ-го признака,
-
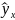теоретич. знач., расчит. по уровню
регрессии.
В частности, параметры уравнения прямолинейной парной регрессии определяются из следующей системы уравнений.
a0 *n + a1Σx = Σy
a0* Σx+a1* Σx²= Σyx
Измерение тесноты корреляционной связи при криволинейных и прямолинейных зависимостях
Определение тесноты связи между результативным и факторным признаками базируется на теории дисперсионного анализа
1. В случае криволинейной зависимости теснота и направление связи между указанными признаками измеряется при помощи индекса корреляции (теоретического корреляционного отношения)
-
факторная дисперсия, кот. Хар-ет вариацию
признака у, обусловленную только фактором
х,
-
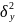общая дисперсия у под влиянием всех
признаков.
2. При линейной зависимости в этих целях используются линейный коэффициент корреляции, который рассчитывается по одной из следующих формул
,
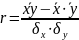
Если R, r → +1, то связь между х и у прямая и тесная (близкая к функциональной)
Если R, r →-1. то обратная и тесная
Если R, r 0, то связь отсутствует