
Семестр 03 / Шпоры на экзамен / 6
.docx|
6.Поле
одной и двух заряженных плоскостей.
1. Поле
полож. Из соображений симметрии вытекает, что напряж-ть поля в любой т. имеет напр-ие, перпендикул. пл-ти. Очевидно, что в симметричных отн-но пл- ти точках напряж-ть поля одинакова по модулю и противоположна по направлению. Представим
цилиндр с образующими, перпендикулярными
пл-ти. В силу симметрии E’
= E’’
= E.
Применим к пов-ти теор. Гаусса (суммарный
поток через пов-ть =
цилиндра,
т.е. на
поля одинакова. Вид линий напряж-ти на рис. Если взять конечную пл-ть, то получ. рез-тат будет справедливым для т., расстояние кот-х от края пластинки значительно превышает расст. от самой пластинки. Хар-р поля на больших расстояниях схож с полем точечного заряда. 2.
Поле 2-х
разноименно заряж. плоск-ей.
Поле 2-х ||-х
величине поверхностной плотностью σ, можно найти как суперпозицию полей, создаваемых каждой из плоск-ей в отдельности. В области между плоск- ями складываемые поля имеют
одинак. напр-ие,
так что результирующая напряж-ть
|

 однородно заряж-й плоск-ти.
Пусть поверхностная плотность q
во всех т. плоск-ти одинакова и = σ; для
опр-ти будем считать q
однородно заряж-й плоск-ти.
Пусть поверхностная плотность q
во всех т. плоск-ти одинакова и = σ; для
опр-ти будем считать q ):
):
 = σ
= σ ,
откуда
,
откуда .
Получ. результат не зав. от длины
.
Получ. результат не зав. от длины расстояниях от пл-ти напряж-ть
расстояниях от пл-ти напряж-ть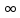 -х
плоск-ей, заряж. разноименно с одинаковой
по абсолютной
-х
плоск-ей, заряж. разноименно с одинаковой
по абсолютной .
Вне объема, ограниченного плоск-ями,
складываемые поля имеют противоположные
напр-ия, так что результирующая
напряж-ть =0. Поле между плоск-ями
однородно, т.к. напряж-ть во всех т.
одинакова. Этот рез-тат справедлив и
для конечных пластин, если расст. между
ними много < их линейных размеров.
.
Вне объема, ограниченного плоск-ями,
складываемые поля имеют противоположные
напр-ия, так что результирующая
напряж-ть =0. Поле между плоск-ями
однородно, т.к. напряж-ть во всех т.
одинакова. Этот рез-тат справедлив и
для конечных пластин, если расст. между
ними много < их линейных размеров.