
- •1 Тема:
- •Тема 3.
- •Свойство однозначности состояния: линейные электрические цепи обладают свойством однозначности электрического состояния всех элементов.
- •Тема 6. Анализ и расчет линейных электрических цепей синусоидального тока.
- •Тема 7. Переходные процессы в линейных электрических цепях. Заряд и разряд конденсатора. Переходный процесс при включении катушки индуктивности на постоянное напряжение.
- •Тема 8. Электромагнитные явления.
- •2 Параллельных провода:
- •Тема 9. Трёхфазные цепи.
- •Тема 12. Асинхронные машины.
- •Тема 12. Синхронные машины (см).
Тема 6. Анализ и расчет линейных электрических цепей синусоидального тока.
Элементы схем замещения цепей синусоидального тока.
Параметры
синусоидально изменяющейся величины:
синусоидальным назыв. ток, кот. изменяется
по закону синуса.
 ,
где
,
где
 - мгновен. знач. тока;
- мгновен. знач. тока;
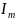 -амплитуда;
-амплитуда;
 - нач. фаза;
- нач. фаза;
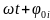 - полная фаза;
- полная фаза;
 – частота. На практике синусоид. величину
выражают постоянным значением –
действующей величиной (
– частота. На практике синусоид. величину
выражают постоянным значением –
действующей величиной ( )
)
Идеальный
резистор в цепи синусоидального
тока: пусть

 для действующ. значений для идеальн.
резистора. Угол сдвига фаз
для действующ. значений для идеальн.
резистора. Угол сдвига фаз
 .
Ток и напряж. совпадают по фазе.
.
Ток и напряж. совпадают по фазе.
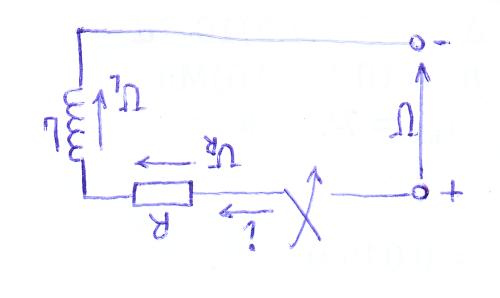
Идеальный
индуктивный элемент в цепи синусоидального
тока: пусть

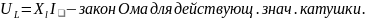
 .
Ток отстает от напряж.
.
Ток отстает от напряж.

Идеальный ёмкостный элемент в цепи синусоидального тока.
Анализ неразветвлённой цепи синусоидального тока. Резонанс напряжений. Анализ разветвлённой цепи синусоидального тока. Резонанс токов. Применение метода комплексных чисел для расчета цепей синусоидального тока.
Тема 7. Переходные процессы в линейных электрических цепях. Заряд и разряд конденсатора. Переходный процесс при включении катушки индуктивности на постоянное напряжение.
Переходные процессы (ПП) - переход эл. цепи из одного состояния в другое в результате изменения параметров её элементов. Изменение не мгновенно, т.к. невозможно скачкообразно измен. энергию магн. и эл. полей. Во время ПП теряется энергия, может возникнуть пробой, нагрев изоляции. ПП использ. в сист. зажигания ДВС, различные импульсные установки.
Методика анализа ПП:
Цель - опред. длительности ПП, зависимости величин тока и напряжения от времени и построение графиков этих зависимостей
Методика: 1. Составляют диф. уравн. по законам КИРХГОФА для мгновенных величин. 2. Подставляют выражения: UR=R*I; UL=L*di/dt; iC=C*duC/dt. 3. Решение диф. ур-ния представляют суммой установившегося значения для нового режима и свободной составляющей (общего решения однородного ур-ния). 4. Пост. интегрирования находят из законов Коммутации.
Законы Коммутации: 1. Ток в цепи с индуктивностью скачком изменится не может iL(-t)=iL(t+). 2. Напряжение на емкости скачком изменится не может Uc(-t)=Uc(t+), где Uc(-t) – напряж. до коммутации; (t+)-после. можно: Uc(-0); (t_)
ПП заканчивается, когда значения равны с точностью 5%. На практике предполагают, что через 3τ заканчивается, где τ-пост. времени.
ПП при вкл. катушки индуктивности на пост. напряжение.
Составляем ур-ние по 2 зак. КИРХ.:
U-UL-UR=0.
U-L*di/dt-R*i=0 :R
 ;
;
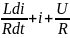 .
.
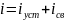
 ток.
Частное
решение :
ток.
Частное
решение :

Общее
решение однородн. ур-ния:
 Правая часть равна нулю, это выражение
- iсв
,
имеем:
Правая часть равна нулю, это выражение
- iсв
,
имеем:
 ,
где
,
где
 – постоянная времени (в сек.). Пост.
интегрирования А найдем ч/з 1ый зак.
коммутации:
– постоянная времени (в сек.). Пост.
интегрирования А найдем ч/з 1ый зак.
коммутации:
 Подставляем:
Подставляем:
 .
Ток после замыкания ключа (после
коммутации) в экспоненциальной ф-ции:
.
Ток после замыкания ключа (после
коммутации) в экспоненциальной ф-ции:

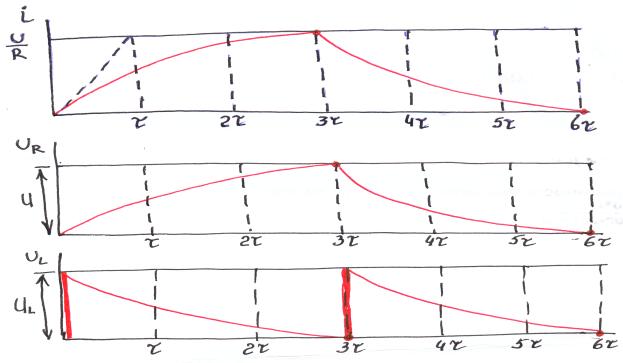
Зарядка и разрядка конденсатора.
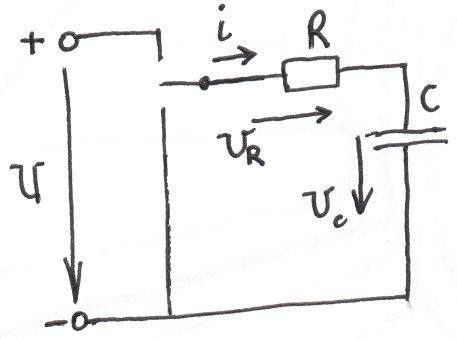
U-UC-UR=0;
U-UC-R*i=0;
U-UC-R*C*duC/dt=0;
RC*duC/dt+UC=U
 -
установившееся
движение,
следоват.
Uуст.
=U
-
установившееся
движение,
следоват.
Uуст.
=U
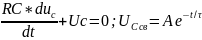
 ,
где τ=RC,
измеряют в сек. Uc=Uсв+Uуст.
,
где τ=RC,
измеряют в сек. Uc=Uсв+Uуст.
 .
.
По
2 зак. коммутации: 0=U+A,
т.к.
 ,
А= -U,
,
А= -U,

