
- •1) Виды проецирования: центральное и параллельное
- •1. Проекции точки. Образование чертежа Монжа - метод Монжа
- •2. Координаты точки
- •3. Две и три проекции точки
- •7. Следы прямой
- •8. Взаимное расположение точки и прямой
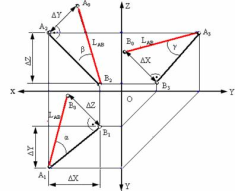
- •9. Определение длин отрезка прямой( натуральная величина отрезка) и углов наклона прямой к плоскостям проекции
- •1) Методом прямоугольного треугольника.
- •10. Взаимное расположение двух прямых
- •11. Взаимно перпендикулярные прямые линии. Теорема о проецировании прямого угла.
- •13. Плоскости частного положения.
- •1. Горизонтальная плоскость уровня - || п1
- •2. Фронтальная плоскость уровня - || п2.
- •3. Профильная плоскость уровня - || п3.
- •15. Главные линии плоскости прямые уровня и линии наибольшего уклона
- •16. Взаимное расположение двух плоскостей.
- •17 Алгоритм решения задачи пересечения двух плоскостей.
- •18. Взаимное расположение прямой и плоскости
- •19. Прямая пересекающая плоскость – алгоритм решения
- •20 Прямая линия перпендикулярная плоскости – теорема о перпендикуляре к плоскости
- •21. Взаимно перпендикулярные плоскости.
- •1. Выпуклые многогранники, их проекции –пирамиды и призмы.
- •2) Пересечение плоскости с многогранником
- •3) Пересечение прямой с многогранником
- •Замена плоскостей проекций – сущность способа.
- •Решение 4 основных задач способом замены плоскостей проекций.
- •Способ вращения – сущность способа.
- •Решение четырех основных задач способом вращения.
- •Проекции плоских кривых.
- •Пространственные кривые – винтовые (цил-ие и кон-ие).
- •Способы образования поверхностей.
- •Каркас и определитель поверхности.
- •Поверхности вращения.
- •Линейчатые развертывающиеся поверхности.
- •Линейчатые поверхности с плоскостью параллелизма.
- •Винтовые поверхности.
- •Циклические поверхности.
- •I способ.
- •II способ.
- •III способ.
- •Пересечение поверхности с плоскостью.
- •Пересечение линии с поверхностью.
- •Пересечение поверхностей. Способ плоских сечений.
- •Пересечение поверхностей. Способ концентрических сфер.
- •Частные случаи пересечение поверхностей второго порядка – теоремы.
- •Плоскости, касательные к линейчатым поверхностям.
- •Плоскости, касательные к кривым поверхностям.
15. Главные линии плоскости прямые уровня и линии наибольшего уклона
Горизонтали, фронтали и профильные прямые, принадлежащие плоскости, называются главными линиями плоскости.
Построение горизонтали h, принадлежащей плоскости, начинают с проведения ее фронтальной проекции h2 перпендикулярно вертикальным линиям связи в области фронтальной проекции плоскости, а горизонтальную проекцию h1 строят из условия принадлежности горизонтали плоскости
Построение фронтали f, принадлежащей плоскости, начинают с проведения ее горизонтальной проекции f1 перпендикулярно линиям связи, в области горизонтальной проекции плоскости, а фронтальную проекцию f2 строят из условия принадлежности
Проекции р1 и р2 профильной прямой р совпадают с одной вертикальной линией связи. При этом на чертеже обозначаются проекции двух точек, принадлежащих одновременно прямой р и плоскости (точки 3 и 4 на рис. 2.3.2).
Очевидно, что через каждую точку плоскости можно провести одну горизонталь h, одну фронталь f и одну профильную прямую р. Вообще же в плоскости можно провести множество горизонталей, фронталей и профильных прямых. Все горизонтали плоскости параллельны между собой, точно также параллельны все фронтали и все профильные прямые.
Линией наибольшего ската плоскости γ называется прямая g, принадлежащая этой плоскости и перпендикулярная ее линиям уровня: горизонтали h и фронтали f
Свойства линии ската:
1) Линия ската на наклонной плоскости есть линия, наибольшего наклона по отношению к горизонтальной плоскости проекций. (Из неравенства: ).
2) Линия ската (линия наибольшего наклона) определяет угол наклона плоскости к горизонтальной плоскости проекций. (Из определения двугранного угла с учетом теоремы о проецировании прямого угла).
3) Линия ската перпендикулярна к горизонталям на наклонной плоскости по отношению к плоскости проекций. (Из условия параллельности любой горизонтали по отношению к линии пересечения наклонной плоскости с плоскости горизонтальной проекций).
16. Взаимное расположение двух плоскостей.
1. параллельные. Две плоскости не имеют общих точек
2. пересекающиеся. две плоскости имеют хотя бы одну общую точку. Пересекающиеся плоскости образуют четыре двугранных угла. Если один из них прямой, тогда и остальные углы тоже прямые, а плоскости называются перпендикулярными
17 Алгоритм решения задачи пересечения двух плоскостей.
Итак, даны две плоскости, заданные треугольниками АВС и DEF. Метод сводится к тому, что бы поочередно найти две точки пересечения двух ребер одного треугольника с плоскостью другого. Соединив эти точки мы получим линию пересечения двух плоскостей. Построение точки пересечения прямой с плоскостью более подробно было рассмотрено в предыдущем уроке, напомню только механические действия:
- Заключим прямую АС во фронтально-проецирующую плоскость и перенесем по линиям связи на горизонтальную проекцию точки пересечения этой плоскости с прямыми DE и DF - точки 1 и 2
- На горизонтальной проекции соединим проекции точек 1 и 2 и найдем точку пересечения получившейся линии с горизонтальной проекцией той прямой, которую мы заключали во фронтально-проецирующую плоскость, в этом случае - с прямой AC. Мы получили точку M.
- Заключим прямую BС во фронтально-проецирующую плоскость и перенесем по линиям связи на горизонтальную проекцию точки пересечения этой плоскости с прямыми EF и DF - точки 3 и 4
Соединим их горизонтальные проекции и получим точку пересечения этой прямой с прямой ВС - точку N.
- Соединив точки M и N мы получим линию пересечения плоскостей заданных треугольниками. По сути линия пересечения уже найдена. - Осталось лишь определить видимость ребер треугольников. Это делается методом конкурирующих точек.
