
Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.
Теорема о приращении функции-??
Связь между непрерывностью и дифференцируемостью функции.
Если функция f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной.
С л е д с т в и е . Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.
П р и м е р .
Функция y = | x | ( рис.3 ) всюду непрерывна, но она не имеет производной при x = 0 , так как в этой точке не существует касательной к графику этой функции. (
Достаточные признаки монотонности функции.
Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.
Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.
Геометрический смысл производной.
Рассмотрим график функции y = f ( x ):
Из рис.1 видно, что для любых двух точек A и B графика функции:
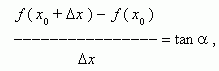
где a - угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x0 , f ( x0 ) ). В общем случае уравнение прямой с угловым коэффициентом f ’( x0 ) имеет вид:
y = f ’( x0 ) · x + b .
Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:
f ( x0 ) = f ’( x0 ) · x0 + b ,
отсюда, b = f ( x0 ) – f ’( x0 ) · x0 ,
и подставляя это выражение вместо b, мы получим уравнение касательной:
y = f ( x0 ) + f ’( x0 ) · ( x – x0 ) .
Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 + точка перемещается на расстояние: x ( t0 + ) - x ( t0 ) = , а её средняя скорость равна: va =
При 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0 ) материальной точки в момент времени t0 . Но по определению производной мы имеем:

отсюда, v ( t0 ) = x’ ( t0 ) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).
2.Правила дифференцирования. Производная сложной и обратной функций.
Правила дифференцирования
Приведем основные правила для нахождения производной:
Производная постоянной равна нулю, то есть c' = 0.
Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, то есть
u(x)± v(x))' = u'(x)± v'(x).
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, то есть
(u(x)v(x))' = u'(x)v(x)+u(x)v'(x).
Следствие 1. Постоянный множитель можно выносить за знак производной:
(cu(x))' = cu'(x).
Производная частного двух дифференцируемых функций может быть найдена по формуле
(u(x)/v(x))' = (u'(x)v(x)-u(x)v'(x))/v2(x)
при условии, что v(x)№ 0.
Дифференцирование сложной и обратной функций
Обратная функция.
Пусть Функция у=f(x) задана на множестве Х=D(f) и Y=E(f). Предположим, что
различным значениям х1 и х2 соответствуют различные
значения функции f(x1) и f(x2). Тогда для любого
уÎУ мы сможем поставить в соответсвие хÎХ| y=f(x). Получает
отображение f-1: У®Х. Это отображение называется обратным.
График прямой и обратной функции симметричен относительно биссектрисы первой и
третьей координатной четверти.
4. Сложная функция.
Пусть заданы две функции t=h(x), [xÎD(h), T=E(h)] и y=g(t),
[tÎT=D(g), Y=E(g)] (область определения одной функции совпадает с
областью значений другой функции и наоборот) Тогда справедливо следующее
правило: из любого хÎХ по правилу ставится в соответствие y=g(h(x)).
Это правило называется сложной функцией.
Производные элементарных функций.
Тупо таблица
Дифференциал функции.
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать D у/D х=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.
Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых ƒ'(х)•∆х и а•∆х, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так кака второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:
Поэтому первое слагаемое ƒ'(х)· ∆х называют главной частью приращения функции ∆у.
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х. (24.1)
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (24.1) можно записать так:
dy=ƒ'(х)dх, (24.2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (24.2) следует равенство dy/dx=ƒ'(х). Теперь обозначение
производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.
