Глава III. Практическая реализация положений организационно-технологической надежности
3.1. Организационная надежность и сетевые модели
Одной из моделей отражения вероятностных производственных процессов является сетевая модель. На сетевом графике можно отразить все технологические и организационные взаимосвязи между элементами строительного процесса. Большим преимуществом сетевого графика является то, что при его расчете из общего количества работ выделяется та цепочка последовательно выполняемых работ, которая и определяет продолжительность процесса в целом. Эта цепочка носит название критического пути. Принадлежащие ей работы называют критическими, все прочие работы – некритическими.
Для анализа сетевой модели применим метод статистических испытаний (метод Монте-Карло). Суть его заключается в многократной реализации вероятностного процесса на модели. По каждой работе сетевого графика определим предельные значения параметров (продолжительности работ) и закон распределения вероятностей наступления значений параметров на интервале предельных значений. Затем, выполняем математическое моделирование вероятного значения параметра с помощью генерирования случайных чисел. Далее сетевой график рассчитываем как детерминированный, определяем одно из значений параметра строительного процесса в целом – продолжительность работ. В результате получается эмпирическое распределение параметров процесса, которое можно подвергнуть любому целенаправленному анализу при необходимости.
Методом статистических испытаний (Монте-Карло) решаем задачу устойчивости критического пути при вероятностной сети.
Сроки работ определяются по формуле:
,
(48)
где αt – случайное число, взятое из таблицы случайных чисел.
Таблица.3.1. Расчёт сроков работ
Код работы |
М (t) |
S (Tкр) |
A |
t ij |
||||
a1 |
a2 |
a3 |
t 1 |
t 2 |
t 3 |
|||
1-2 |
10 |
2 |
0,2005 |
-0,5564 |
0,4043 |
10,401 |
8,88 |
10,80 |
1-3 |
32 |
3 |
1,1609 |
1,7981 |
0,4688 |
35,48 |
37,39 |
33,40 |
1-4 |
11 |
3 |
0,5864 |
0,427 |
0,8115 |
12,75 |
12,28 |
13,45 |
2-5 |
38 |
2 |
0,1425 |
-0,7679 |
0,5405 |
38,28 |
36,46 |
39,08 |
2-6 |
14 |
2 |
0,9516 |
-0,0077 |
-1,1929 |
15,90 |
13,98 |
11,61 |
3-4 |
0 |
0 |
-0,5863 |
0,8115 |
0,0093 |
0,00 |
0,00 |
0,00 |
3-6 |
13 |
4 |
1,1572 |
0,0904 |
0,4167 |
17,62 |
13,36 |
14,66 |
4-6 |
16 |
4 |
-0,4428 |
1,2809 |
0,5154 |
14,22 |
21,12 |
18,06 |
4-7 |
12 |
3 |
-0,3934 |
2,8854 |
0,2005 |
10,81 |
20,65 |
12,60 |
5-8 |
10 |
2 |
0.8319 |
-0,5557 |
1,1603 |
11,66 |
8,08 |
12,32 |
6-5 |
0 |
0 |
-1,7708 |
1,4664 |
0,2005 |
0,00 |
0,00 |
0,00 |
6-7 |
8 |
1 |
1,1922 |
-0,5098 |
0,1425 |
9,19 |
7,49 |
8,14 |
6-8 |
13 |
4 |
-0,6690 |
0,6141 |
0,3516 |
10,32 |
15,45 |
16,80 |
6-9 |
35 |
4 |
-0,245 |
-0,8888 |
-0,5863 |
34,02 |
31,44 |
32,65 |
7-9 |
17 |
5 |
-0,2863 |
0,8960 |
1,1572 |
15,56 |
21,48 |
22,78 |
8-9 |
0 |
0 |
1,2809 |
-0,8513 |
-0,5863 |
0,00 |
0,00 |
0,00 |
8-10 |
26 |
2 |
0,8574 |
0,5816 |
-0,3954 |
27,71 |
27,16 |
25,21 |
9-10 |
17 |
3 |
0,9900 |
1,5068 |
0,8315 |
19,99 |
21,52 |
19,49 |
Сетевая модель 1-го варианта Ткр1=107,12ед.
Рис. 3.1.1
Сетевая модель 2-го варианта Ткр2=111,47ед.
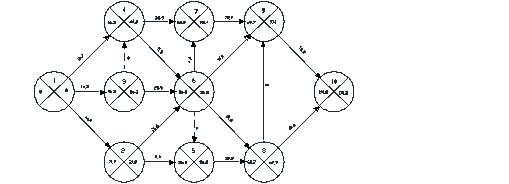
Рис.3.1.2
Сетевая модель 3-го варианта Ткр3=110,8ед
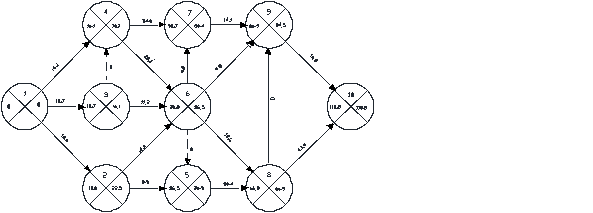
Рис.3.1.3
Ткр1 = 139,32
Ткр2 = 118,92
Ткр3 = 101,11
Ткр4 = 107,12
Ткр5 = 119,78
Ткр6 = 107,00
Ткр7=110,3
Ткр8=110,8
Доверительные границы критического пути, т.е. устойчивость критического пути как статистической вероятности его прохождения по определённым событиям при заданной вероятности p = 0,98 , λ = 3,02 соответственно определяются по следующим формулам:
Далее находим максимальное и минимальное значения критического пути при заданной вероятности p = 0,98 , λ = 3,02
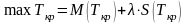(49)
(50)
Tmax=114,29+3,02*4,61=128,21.
Tmin=114,29-3,02*4,61=100,36.
Все вычисленные величины наносим на график, который представлен на рис.3.3.
