13. Вычисление электростатических полей в вакууме с

помощью теоремы Гаусса

Необходимо усвоить 2 основополагающих момента, относящихся к интегральной форме теоремы Гаусса:

1.Теорема Гауссав вакуумеверна всегда.

2.Интегральная форма теоремы Гаусса для вычисленияполезна не всегда, а только тогда, когда из симметрии задачи удается найти и описать простые эквипотенциальные поверхности.

Вопр. Почему интересуемся эквипотенциальными поверхностями?

Отв.Т.к. в каждой их точкеперпендикулярно, а это превращаетв произведение:=. Именно в этих случаях использование интегральной формы теоремы Гаусса существенно облегчает расчет распределенияв пространстве.

Вспомним, в каких решенных нами задачах и для каких заряженных объектов существовали простые по форме эквипотенциальные поверхности:

точечный заряд, заряженный шар, шаровой слой – концентрические сферы;

заряженная нить, цилиндр; цилиндрический слой – коаксиальные цилиндрические поверхности;

бесконечная заряженная плоскость, набор параллельных заряженных плоскостей, бесконечный заряженный слой – параллельные плоскости.

Практически это все задачи, при решении которых нам будет помогать теорема Гаусса.

1) Поле бесконечной однородно заряженной плоскости.

Пусть бесконечная по осямyиzплоскость заряжена равномерно с поверхностной плотностью -.

Найдем распределение напряженности электрического поля и потенциала в пространстве.

Изобразим силовые линии напряженности поля вблизи пластины. В силу симметрии задачи можем воспользоваться теоремой Гаусса для расчета, для этого выберем цилиндрическую поверхность, как показано на рисунке. При этом основания цилиндра должны быть расположены на одинаковом расстоянии от заряженной плоскости. Тогда поток полябудет пронизывать только основания цилиндра, причем, в силу симметрии задачи потоки через левое и правое основания будут одинаковы, т.к..

По теореме Гаусса: поток напряженности поля через поверхность нашего цилиндра равен стороннему заряду, находящемуся внутри цилиндра, деленному на.

Здесь - площадь основания цилиндра.

Т.к. линии поля втекают в цилиндр, то- внешние нормали

анти параллельны линиям поля, поэтому имеем:

-поле бесконечной заряженной плоскости однородно.

Найдем распределение потенциала:

Вопр.В данном случае работа сил поля по удалению единичного точечного положительного заряда из любой точки на бесконечность отрицательна, т.к., а полученный нами потенциал положительный. В чем дело?

Отв.Потенциал имеет указанный смысл работы по удалению единичного точечного положительного заряда из любой точки на бесконечность только в том случае, если потенциал нормирован на бесконечности, а это возможно только для конечной системы зарядов, в нашем случае на плоскости сосредоточен бесконечный заряд, поэтому и потенциал занулить на бесконечности невозможно.

2) Поле 2-х заряженных плоскостей.

Изобразим силовые линии напряженности каждой плоскости и воспользуемся принципом суперпозиции. Из рисунка => снаружи , внутри.

Этот результат можно получить с помощью теоремы Гаусса , вычисляя поток через поверхности изображенных на рисунке цилиндров.

Снаружи: Внутри:

, если положить=0.

3) Поле заряженного слоя (неравномерно заряженный слой).

Внутри слоя:

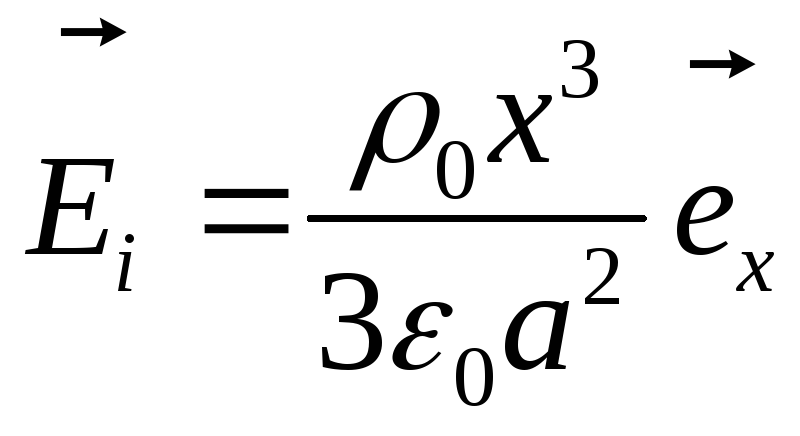
Снаружи слоя:

Постоянная интегрирования С находится из условия сшивки потенциала в точках

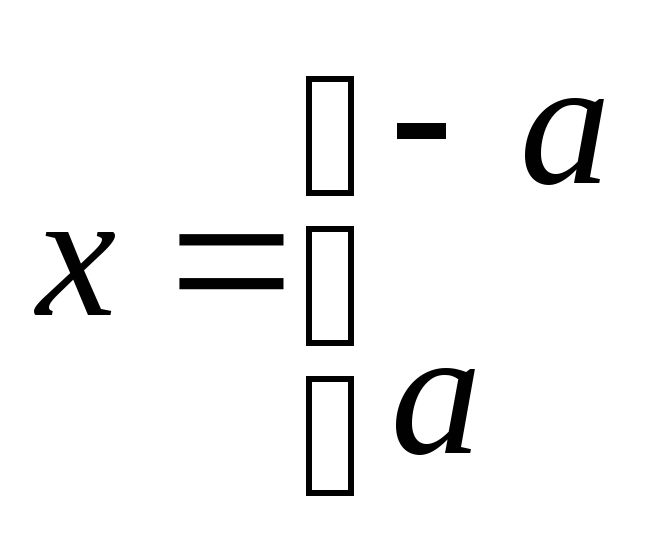
В случае объемного распределения заряда в отсутствии диэлектриков потенциал является не только непрерывной, но и гладкой функцией, не имеющей изломов.

4) Поле цилиндра (однородно заряженного).

Внутри:

При , но так, чтобы, имеем поле бесконечной заряженной нити

5)Поле шара.

А) Однородно заряженный шар плотностью заряда -.

Внутри шара:

Вне шара:

;

С находится из условия сшивки потенциала вне и внутри шара на границе областей

При , но так, что, имеем поле точечного заряда

.

Б) Заряд распределен неравномерно - радиус шара.

Внутри шара:

Вне шара:

Потенциал внутри шара:

Из условия непрерывности потенциала: