8. Работа сил электростатического поля

убыли потенциальной энергии.

Если поле создается конечным зарядом, распределенным по конечной области пространства, тоТогда, т.е. в этом случае:

потенциал в любой точке поля, создаваемого конечным зарядом, распределяемым по конечной области пространства, равен работе сил электростатического поля по перемещению единичного положительного точечного заряда из данной точки на .

За единицу потенциала, называемую 1В, принимают потенциал в такой точке поля, для перемещения в которую из точечного заряда в 1Кл надо совершить работу в 1Дж.

9. Задачи на вычисление и.

1). Точечный зарядq

Потенциал и напряженность поля отрицательного заряда q<0 – отрицательные, т.к.при движении к.

Эквипотенциальными поверхностями точечного заряда являются сферы.

2). Поле заряженного стержня.

- поле заряженного стержня на прямой, перпендикулярной к нему и проходящей через его середину.

Вопр. Что же получается, при?

Отв. Надо правильно осуществлять переход: конечно, если размазать конечный зарядqпо бесконечному стержню, то получим 0, а надо сделать так:

-поле бесконечной заряженной нити.

Поле цилиндрической поверхности, осью которой является заряженная нить.

.

Эквипотенциальными поверхностями бесконечной заряженной нити являются коаксиальные цилиндрические поверхности, осью которых является заряженная нить.

3). Поле кольца.

Максимум исследовать самостоятельно.

4). Поле дискаR,q

Поверхностная плотность заряда .

Рассмотрим кольцо (r,r+dr;), его заряд

Поле, создаваемое этим кольцом на его оси на расстоянии х от центра кольца:

приx>>R

При имеем-это поле бесконечной заряженной плоскости.

Эквипотенциальными поверхностями бесконечной заряженной плоскости являются плоскости, параллельные данной заряженной плоскости.

10. Энергия взаимодействия зарядов

. ВсегоNзарядов.

т.к. акт взаимодействия был учтен дважды.

Или, иначе, откуда берется:

получена при суммировании пар слагаемых:

=> по третьему закону Ньютона =>

в общей при этом будетслагаемых, а неN=>.

11. Элементы векторного анализа

1) Поток векторного поля

Математический аппарат для описания свойств векторных полей называется векторным анализом. Векторные поля, в том числе электростатические и магнитные обладают рядом свойств, которые облегчают их вычисление. С одним из этих свойств мы сейчас познакомимся.

1)Поток вектора.

Пусть векторное полев любой точке пространства задан

Возьмем площадку , ориентация которой в пространстве будет определяться нормалью, вообще говоря, в любой точке.

- векторк поверхности в данной точке.

Если уменьшать , то разнонаправленностьсольется в один вектор единичной длины =>, т.к. малый элемент поверхности ( стянутый в точку) будет характеризоваться единой. Тогда потокомчерезназывают.

Это алгебраическая скалярная величина, которая зависит от выбора направления нормали. В случае замкнутых поверхностей принято выбирать внешнюю нормаль, т.е. направленную наружу области, охватываемой данной замкнутой поверхностью.

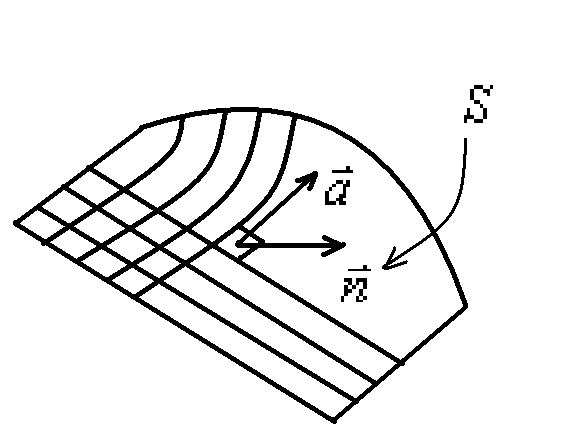
Чтобы лучше себе представить себе, что такое поток, достаточно рассмотреть:

1). Поле скоростей в потоке жидкости: пусть- скорость струи жидкости.

Тогда Ф будет определять собой объем жидкости, протекающий через площадь S

в единицу времени.

Скалярное произведение означает, что, как бы вы не поставили невод, перегораживая реку, объем воды, протекающий через невод в единицу времени, не изменяется.

- объем

Поток численно равен числу линий поля, пересекающих данную поверхность.

Поток вектора через замкнутую поверхность:

= 0, если внутри нет источников поля ;

, если внутри поверхности есть источники поля. Представим себе проволочный шар, а лучше куб, который лежит на дне реки, поток через его поверхность:

а) Ф0, если внутри бьет родник;

б) Ф=0, если родника внутри нет.

2). Поле скоростей потока зарядов: пусть- плотность зарядов в пучке,- скорость зарядов, тогда- плотность тока

- ток через поверхностьS.

2) Дивергенция-удельная мощность источников векторного поля в данной точке.

Свойства : 1) скалярная функция векторного аргумента;

2) локальная характеристика поля;

3) аддитивная функция .

4)

Дивергенция - это оператор, который действует на векторную величину следующим образом:

в декартовой системе координат;

=в цилиндрической системе координат;

в сферической системе координат.

Докажем это для простейших случаев:

1)

2)

- ч.т.д.