2. Вычисление объема тела вращения

Объем тела, образованного вращением криволинейной трапецией вокруг оси , которая ограниченной кривой , осью и двумя прямыми и , находится по формуле

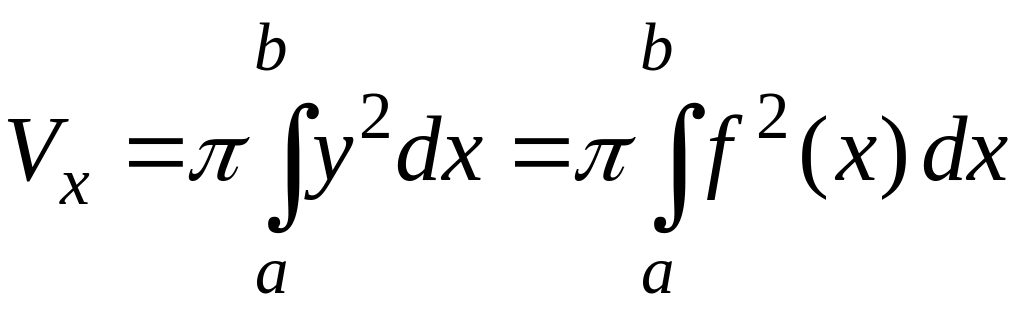. (2.9)

2. Вычисление длины дуги

Длина гладкой кривой между двумя точками с абсциссами и , находится по формуле

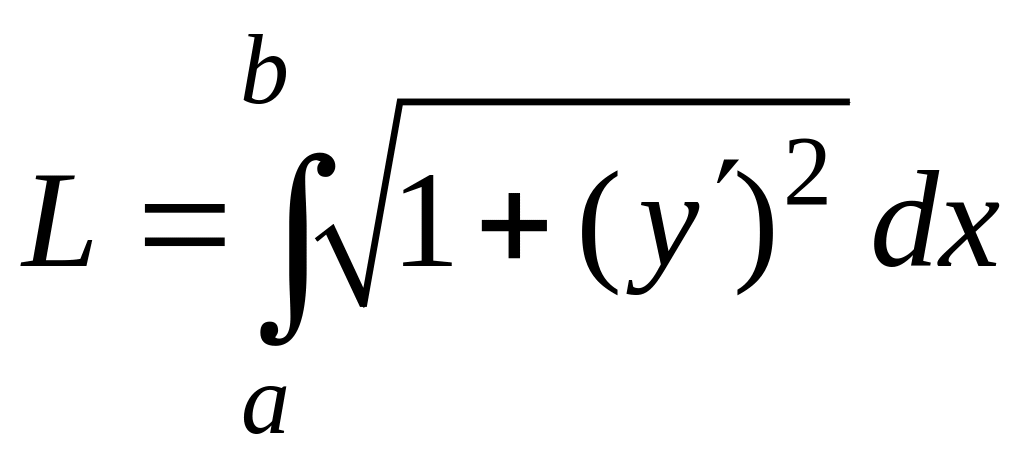. (2.10)

4. Приложения определенного интеграла в экономике

Согласно свойству 5 (теореме о среднем) справедливо равенство

,

где точка .

Число называется средним значением функции на отрезке . На практике нередко вычисляются такого рода средние значения, например, средняя производительность труда, средняя мощность электродвигателей и т.д.

Рассмотри на примере.

Пример 2.5. Найти среднее значение издержек , выраженных в денежных единицах, если объем продукции меняется от 0 до 3 единиц. Указать объем продукции, при котором издержки принимают среднее значение.

Решение. Применим теорему о среднем значении. Тогда

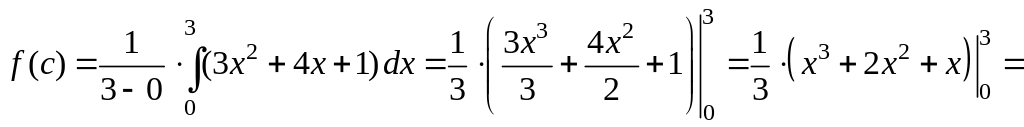
(ден. ед.).

Таким образом, среднее значение издержек равно 16.

Определим, при каком объеме продукции издержки принимают это значение. Решаем уравнение

 .

Учитывая, что объем продукции не может быть отрицательным, из последнего уравнения имеем единиц продукции.



Приведем еще несколько случаев использования определенного интеграла в экономике:

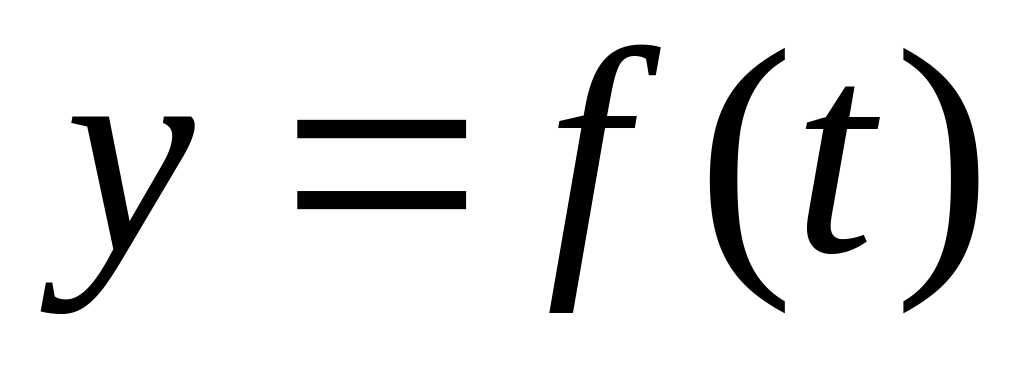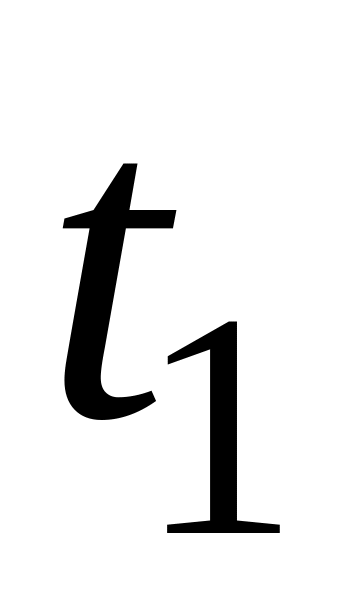• Если непрерывная функция характеризует изменение производительности от времени , то объем продукции, произведенной рабочим за промежуток времени от до 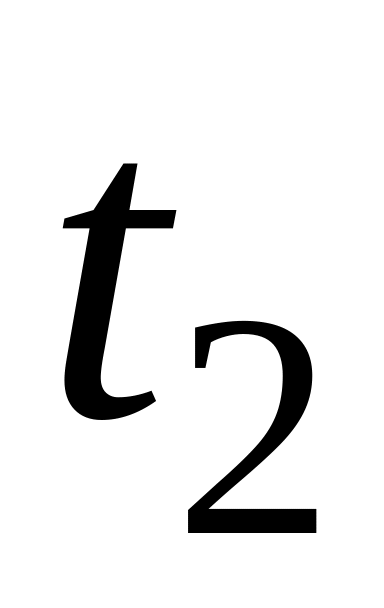, находится по формуле

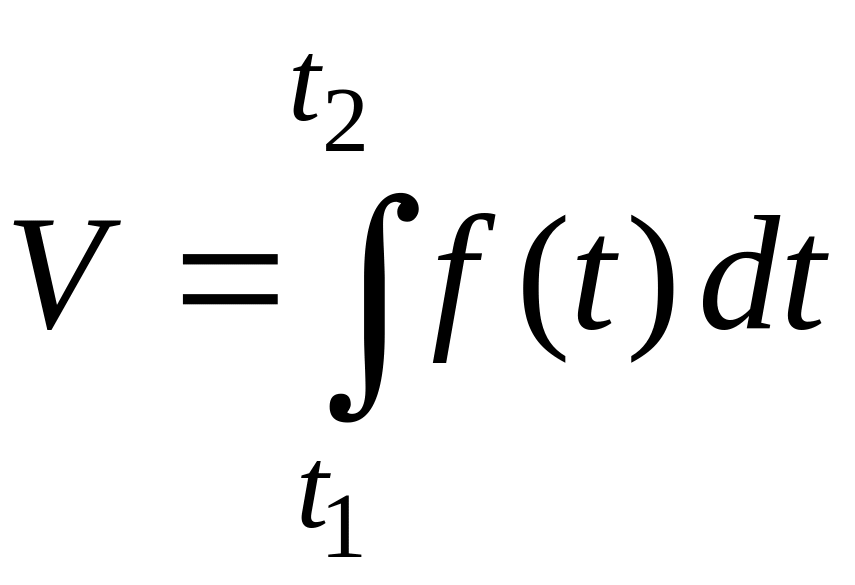. (2.11)

• Если непрерывная функция характеризует поток платежей от времени , то объем платежей за промежуток времени от до , находится по формуле

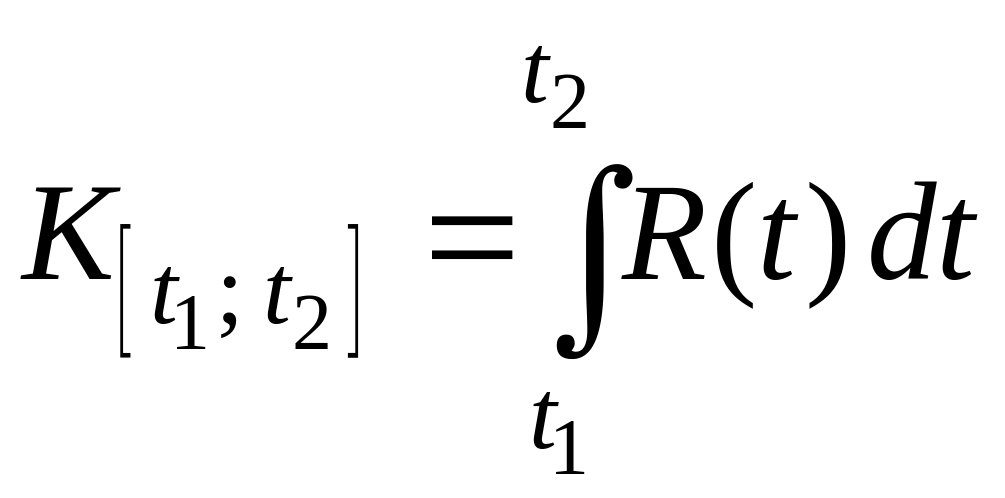. (2.12)

Пример 2.6. Определить объем продукции, произведенной рабочим за второй час рабочего дня, если производительность труда характеризуется функцией

.

Решение. Согласно формуле (2.11) получаем



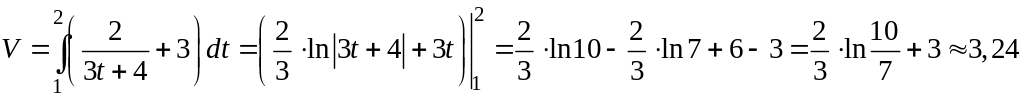
3. Несобственный интеграл

До сих пор при рассмотрении определенного интегралов считали, что промежуток интегрирования конечен и что подынтегральная функция на нем непрерывна. Определенный интеграл , где промежуток интегрирования конечный, а подынтегральная функция непрерывна на отрезке , называется еще собственным интегралом. Если хотя бы одно из условий не выполнимо, то интеграл называется несобственным. Собственный интеграл всегда имеет определенное численное значение. В отличие от этого несобственные интегралы не всегда имеют такое значение.

3.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл первого рода)

Определение 3.1. Пусть функция непрерывна на промежутке . Если существует конечный предел 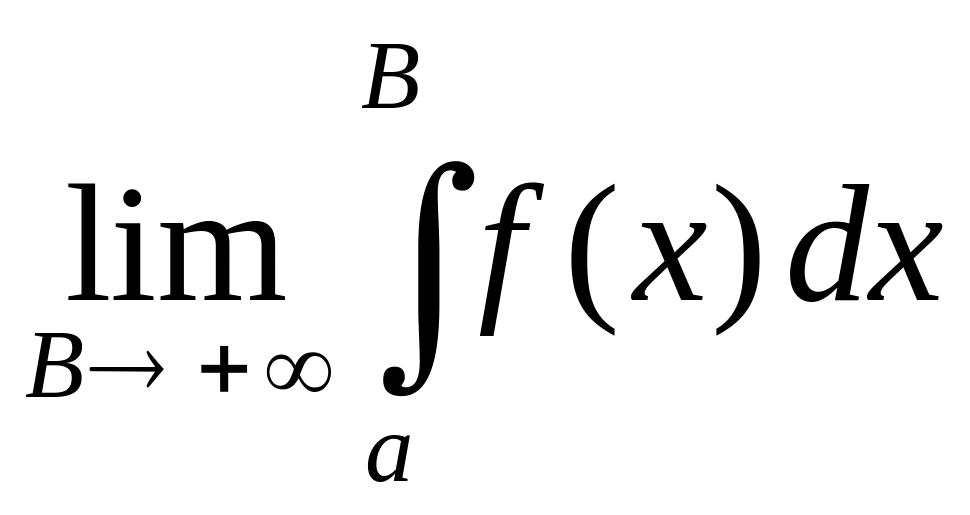, то его называют сходящимся несобственным интегралом первого рода и обозначают 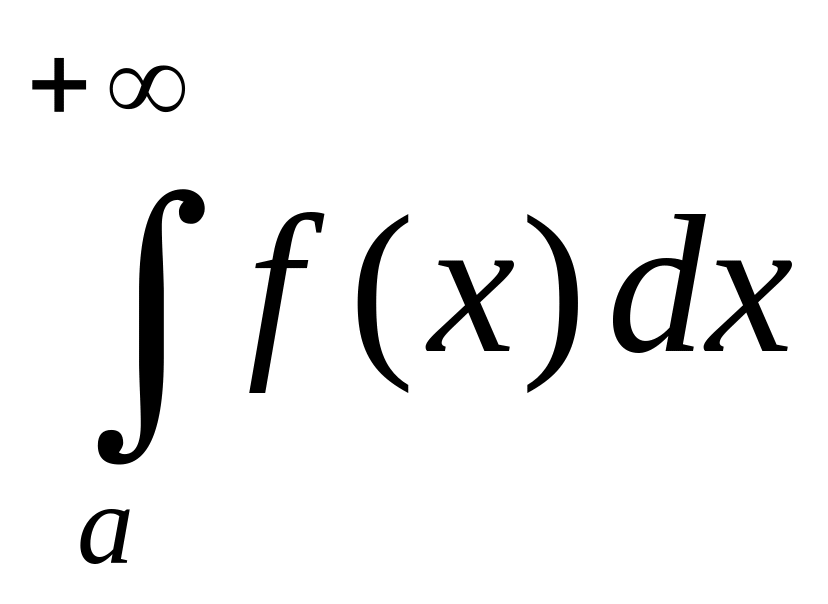, т.е.

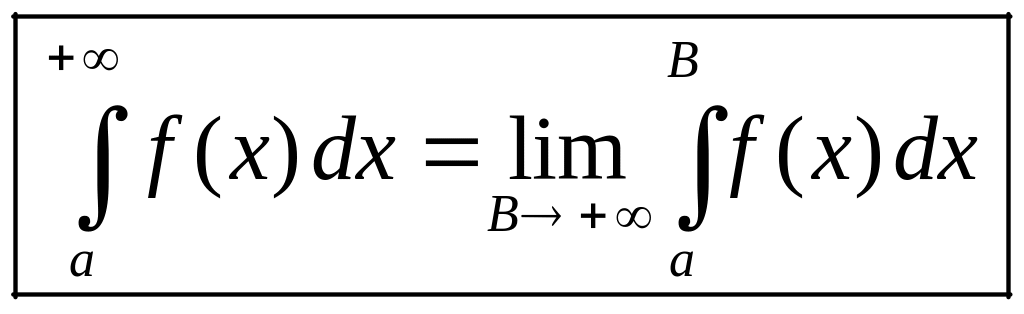. (3.1)

Если же указанный предел не существует или он бесконечен, то говорят, что интеграл расходится.

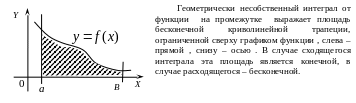
Аналогично определяется несобственный интеграл на промежутке :

.

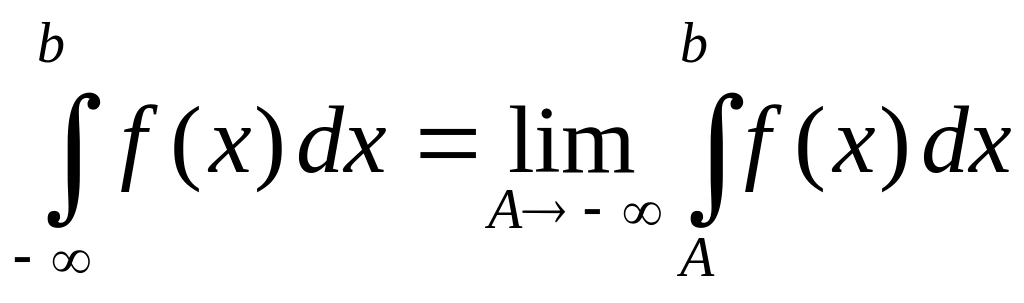Несобственные интегралы с двумя бесконечными пределами определяются формулой

,

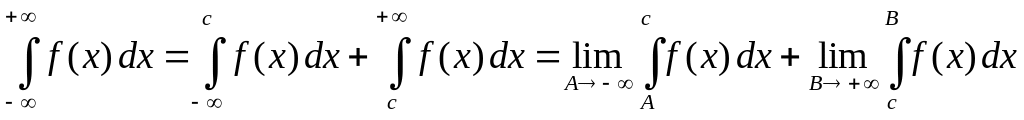где  произвольное число.

Пример 3.1. Дан интеграл 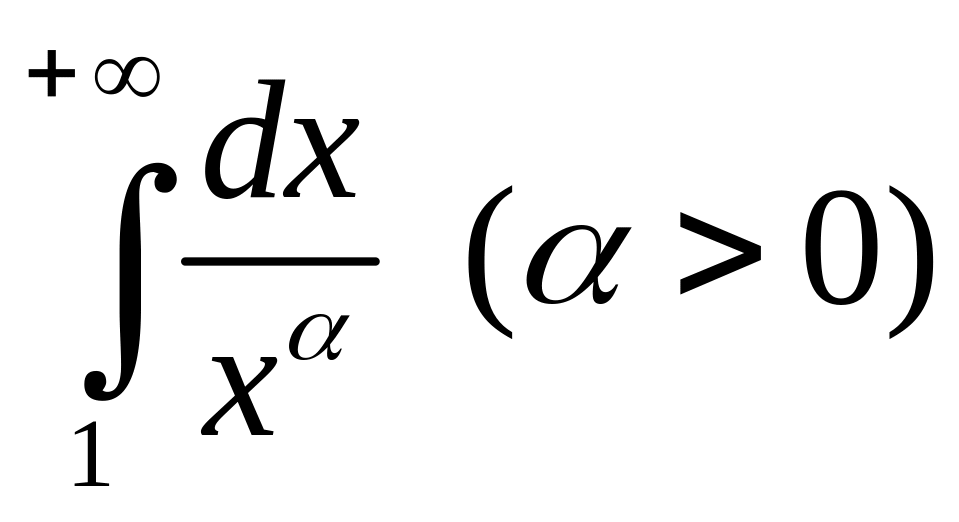. Установить, при каких значениях этот интеграл сходится, а при каких – расходится.

Решение. Предположим, что . Тогда

.

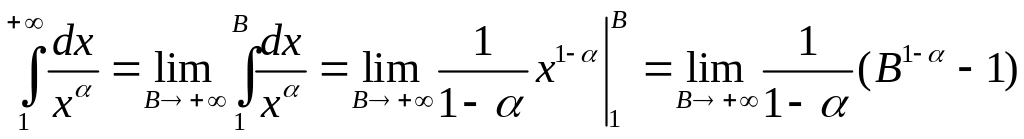Следовательно, если , то , т.е. данный интеграл сходится.

Если , то 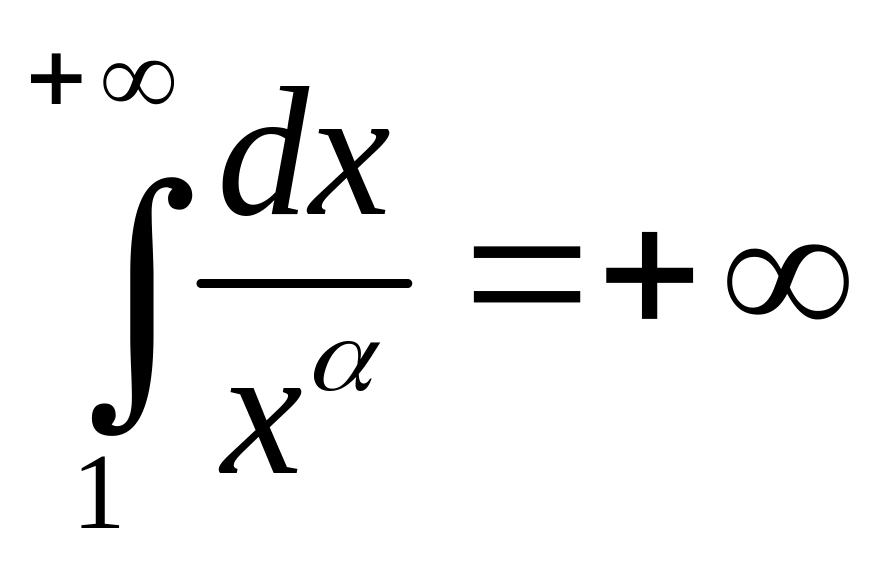, т.е. интеграл расходится.

При имеем 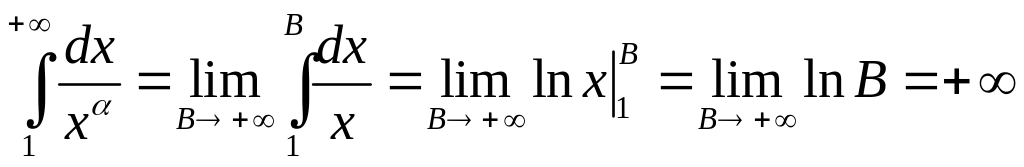, т.е. данный интеграл расходится.



Пример 3.2. Вычислить несобственный интеграл или установить его расходимость:

,

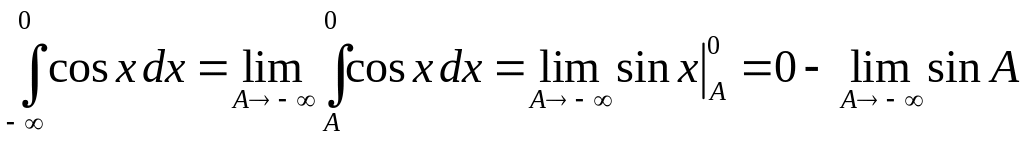интеграл расходится, так как при предел не существует.



Замечание. При вычислении несобственных интегралов с бесконечным промежутком интегрировании часто пользуются символическим равенством

,

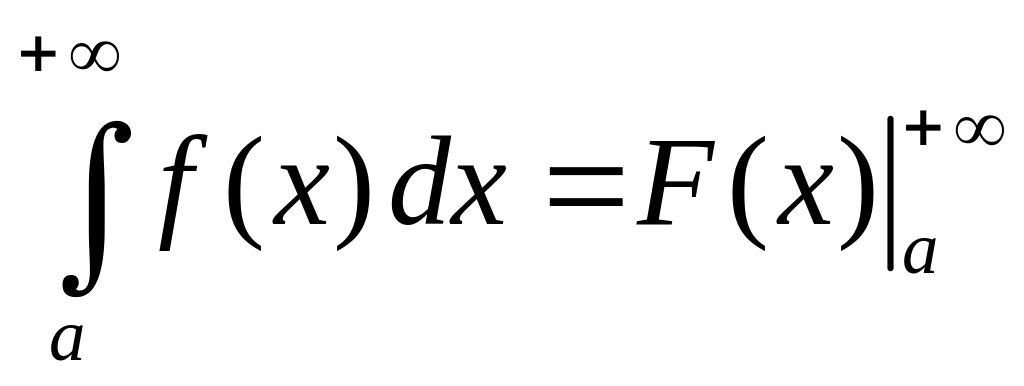где и .

Пример 3.3. Вычислить несобственный интеграл или установить его расходимость:

,

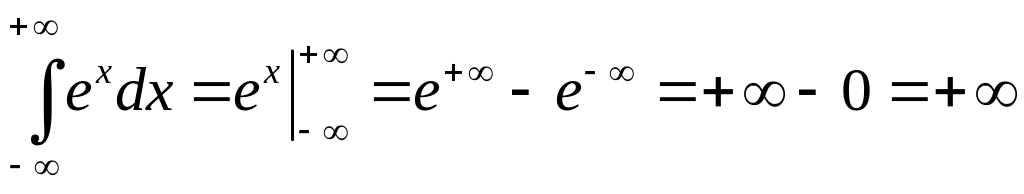т.е. данный интеграл расходится.



В некоторых задачах нет необходимости вычислять интеграл; достаточно лишь знать, сходится ли он или нет. Приведем без доказательства один из признаков сходимости.

Теорема 3.1 (признак сравнения). Если на промежутке непрерывные функции и удовлетворяют условию , то

1) если сходится 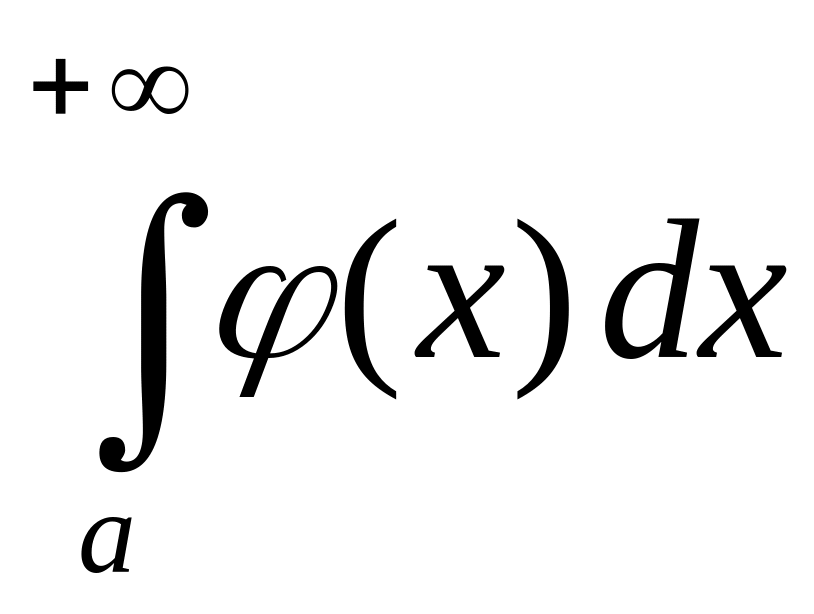интеграл , то сходится и интеграл ;

2) если расходится интеграл , то расходится и интеграл .

Пример 3.4. Доказать, что интеграл 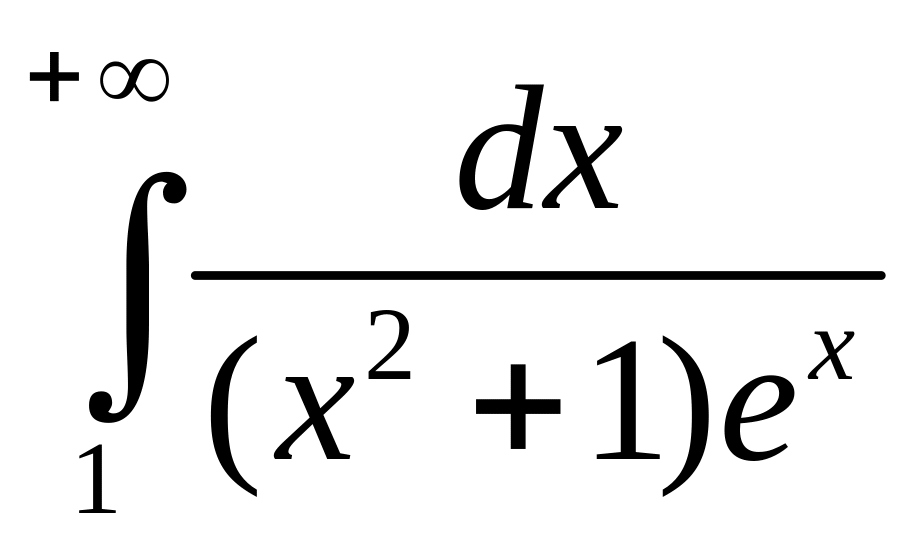сходится.

Доказательство. Так как 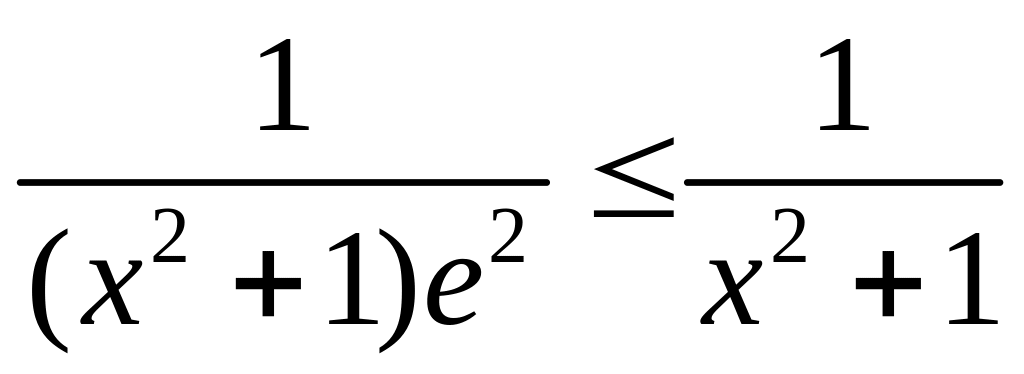при и интеграл

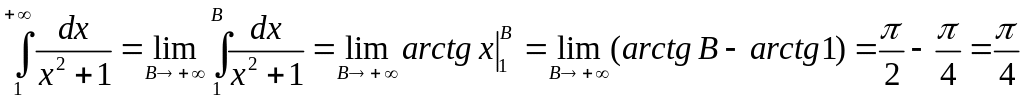
сходится, то исходный интеграл также сходится.

