1.11. «Берущиеся» и «неберущиеся» интегралы
I. О технике интегрирования
Как уже отмечалось выше, операция интегрирования функций значительно сложнее операции дифференцирования функций. Не всегда выбранный путь интегрирования является наилучшим, более коротким, простым. Интегрирование часто может быть выполнено не единственным способом. Всякий раз частные обстоятельства должны подсказать тот искусственный прием, который в данном случае быстрее приводит к цели. Владение операцией интегрирования заключается не только в знании того, как можно, в конце концов найти данный интеграл, но и в умении взять его с минимумом затраченного времени и труда.
Например,
можно найти, не используя рекомендуемую
подстановку
,
а применив искусственный прием:
.
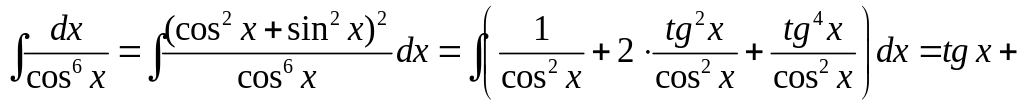
Вряд ли стоит вычислять интеграл
,
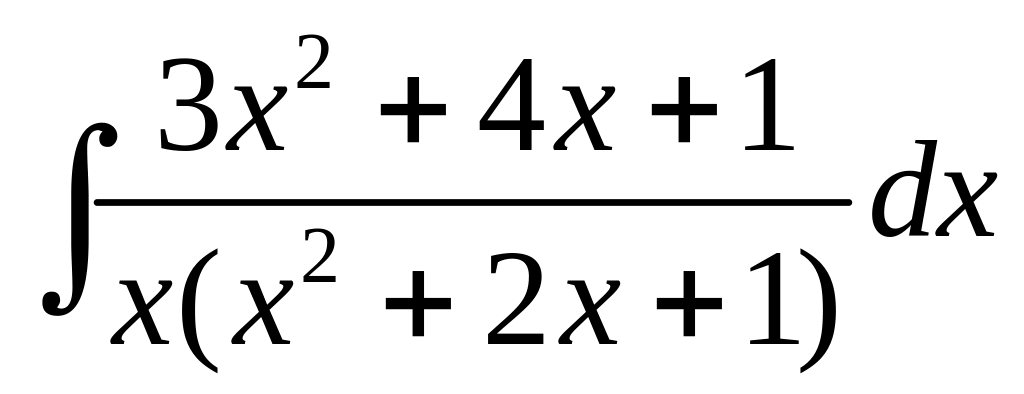разлагая подынтегральную функцию на
простейшие дроби. Заметив, что числитель
является производной знаменателя
,
легко получить:
.
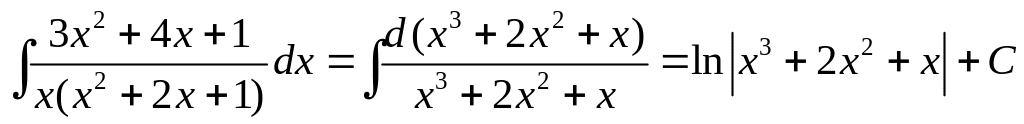II. Использование таблиц интегрирования
Изученные методы интегрирования состоят в преобразованиях, приводящих данный интеграл к интегралу, заранее известному, т.е. находящемуся в известной таблице интегралов. До сих пор пользовались только самой краткой основной таблицей интегралов. Но ясно, что чем более полной таблицей интегралов мы имеем возможность пользоваться, тем проще и короче делается само интегрирование.
В практических целях часто употребляются различные справочники и готовые таблицы особенно часто встречающихся интегралов.
III. Об интегрировании в элементарных функциях
Как известно, всякая непрерывная
функция имеет первообразную. В том
случае, когда первообразная некоторой
элементарной функции
является также элементарной функцией,
говорят, что
«берется», т.е. интеграл выражается
через элементарные функции (или интеграл
вычисляется). Если же интеграл не
выражается через элементарные функции,
то говорят, что интеграл «не берется»
(или «его найти нельзя»).
Например, нельзя найти интеграл
,
так как не существует элементарной
функции, производная от которой была
бы равна
.
Приведем примеры «неберущихся»
интегралов, которые имеют большое
значение в приложениях:
интеграл Пуассона (теория вероятностей);
интегральный логарифм (теория чисел);
интегралы Френеля (физика);
интегральные синус и косинус.
Первообразные от функций
и других хорошо изучены, для них составлены
подробные таблицы значений для различных
значений аргумента
.
2. Определенный интеграл
2.1. Понятие определенного интеграла
Пусть функция
определена на отрезке
,
причем
.
Разобьем отрезок
на
частичных отрезков
,
,
…,
.
В каждом частичном отрезке
выберем произвольную точку
и вычислим значение функции в ней, т.е.
.
Далее составляем сумму
:
,
(2.1)
где
длина соответствующего
частичного отрезка.
Сумма вида (2.1) называется интегральной
суммой функции
на отрезке
.
Обозначим через
длину наибольшего из частичных отрезков,
т.е.
,
.
Найдем предел интегральной суммы (2.1),
когда
так, что
.
Определенным интегралом от
функции
на отрезке
называется конечный предел ее интегральной
суммы, когда число частичных отрезков
неограниченно возрастает, а длина
наибольшего из них стремится к нулю.
Определенный интеграл обозначается
символом
.
Таким образом,
.
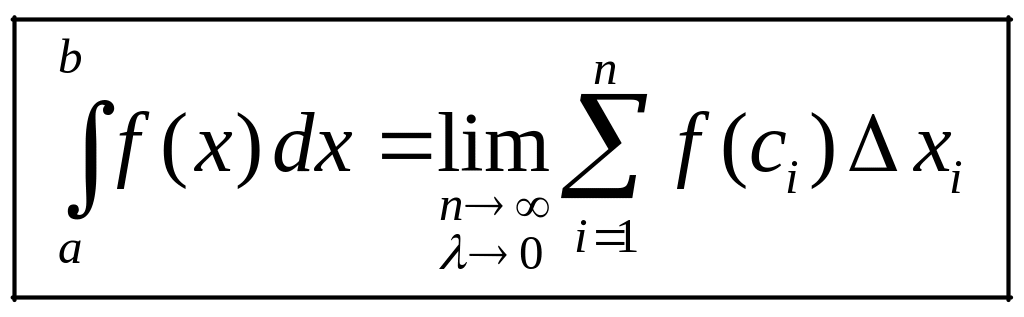(2.2)
Числа
и
называются соответственно нижним
и верхним пределами интегрирования,
подынтегральной
функцией,
подынтегральное
выражение,
переменной
интегрирования, отрезок
областью
(отрезком) интегрирования.
Функция , для которой на отрезке существует определенный интеграл , называется интегрируемой на этом отрезке.
Сформулируем теорему существования определенного интеграла (без доказательства).
Теорема 2.1 (Коши). Если функция непрерывна на отрезке , то определенный интеграл существует.
Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечной число точек разрыва.
Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения.
1) Определенный интеграл не зависит от обозначения переменной интегрирования:
.
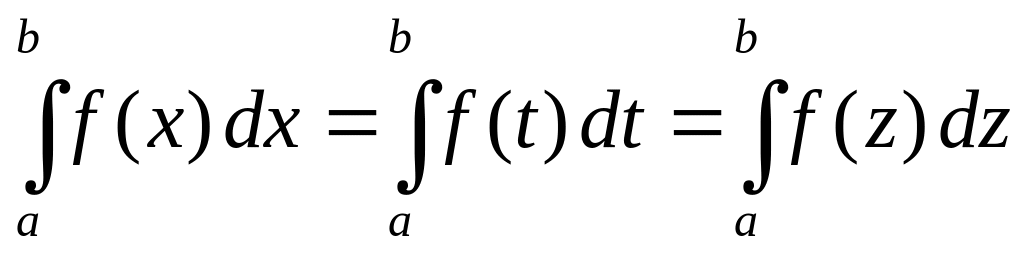2) Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
.
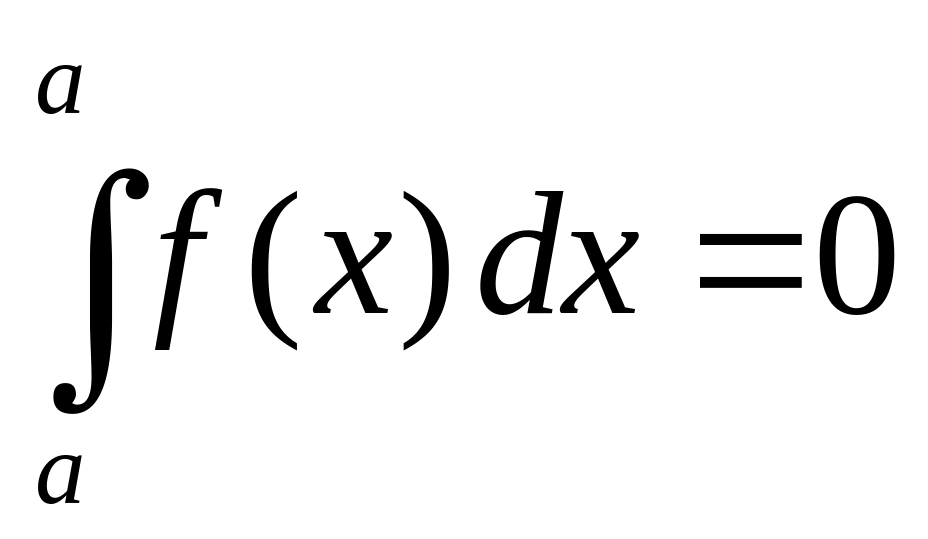3) Для любого действительного числа
:
.
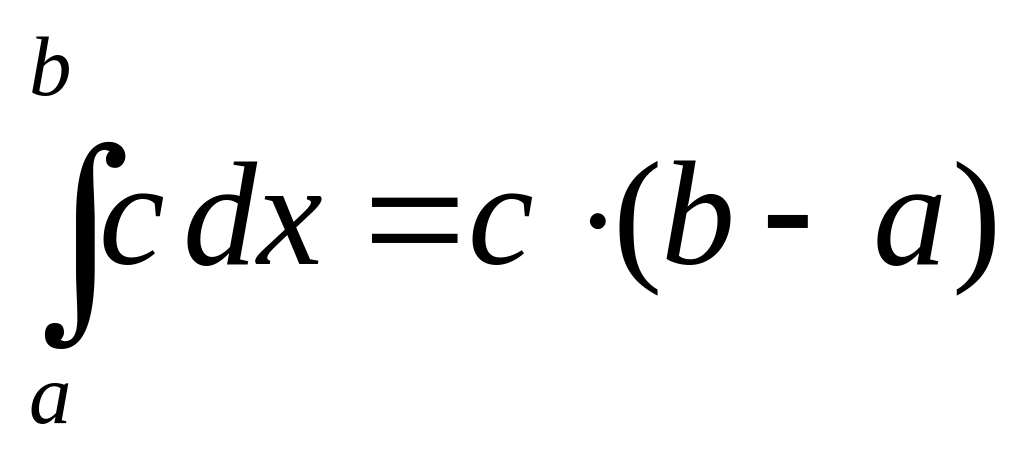Геометрический смысл определенного интеграла: определенный интеграл от неотрицательной функции на отрезке численно равен площади криволинейной трапеции.