1.7. Дробно-рациональная функция

Определение 1.3. Дробно-рациональной функцией (или рациональной дробью) называется функция, равная отношению двух многочленов, т.е. 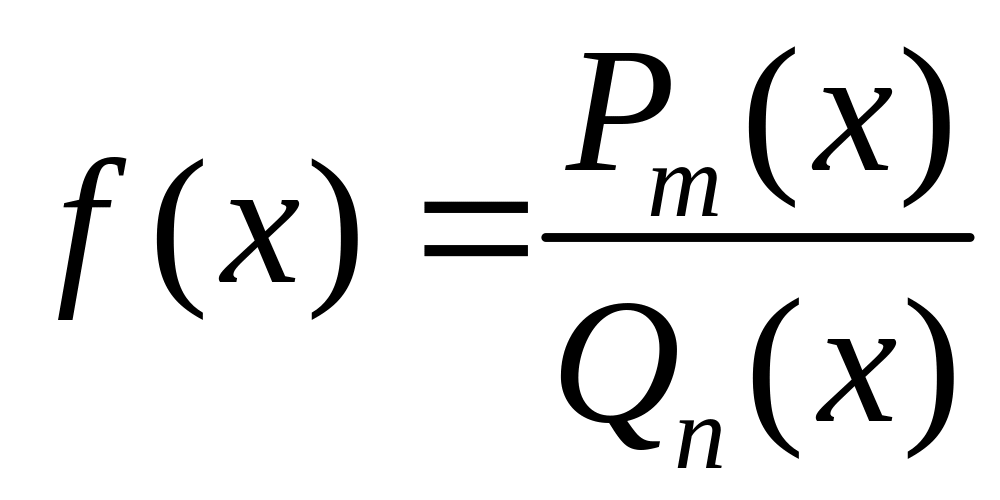, где  многочлен степени , а  многочлен степени .

Определение 1.4. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, т.е. , в противном случае (если ) рациональная дробь называется неправильной.

Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена и правильной рациональной дроби , т.е.

.

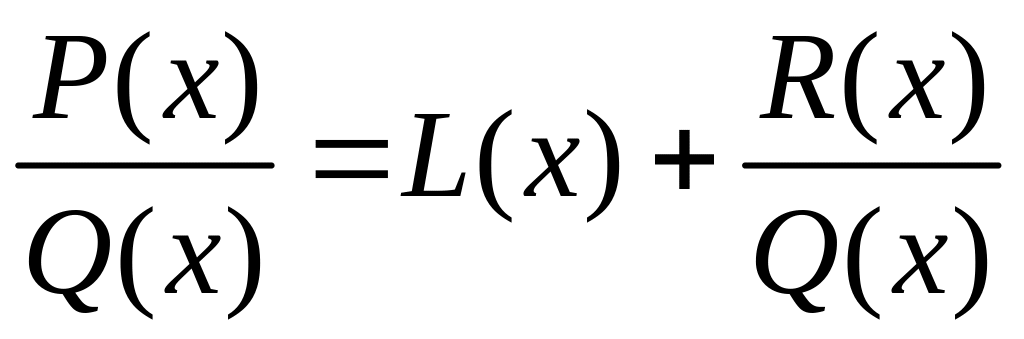Данный прием используется при нахождении некоторых интегралов, содержащих рациональную дробь.

Пример 1.5. Найти интеграл .

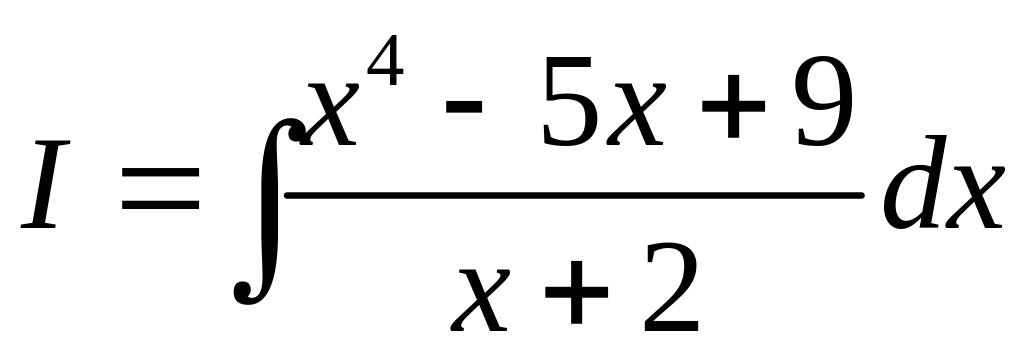Решение. Сначала разделим числитель на знаменатель в столбик:

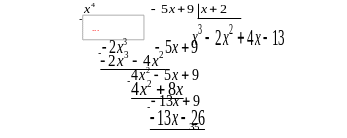
Значит, . Далее находим интеграл:



Определение 1.5. Правильные рациональные дроби вида

(I) ;

(II) ;

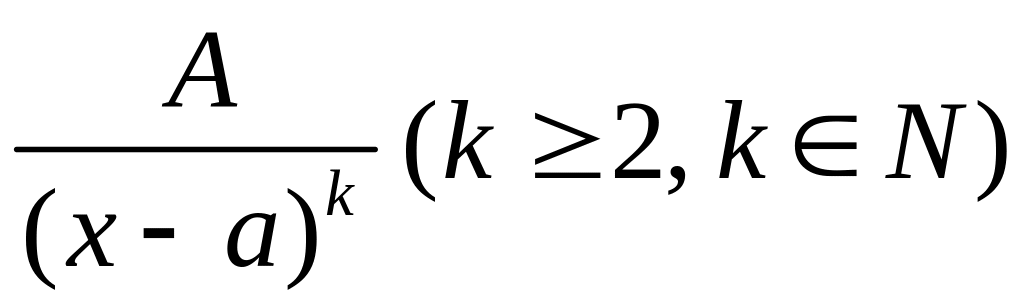(III) 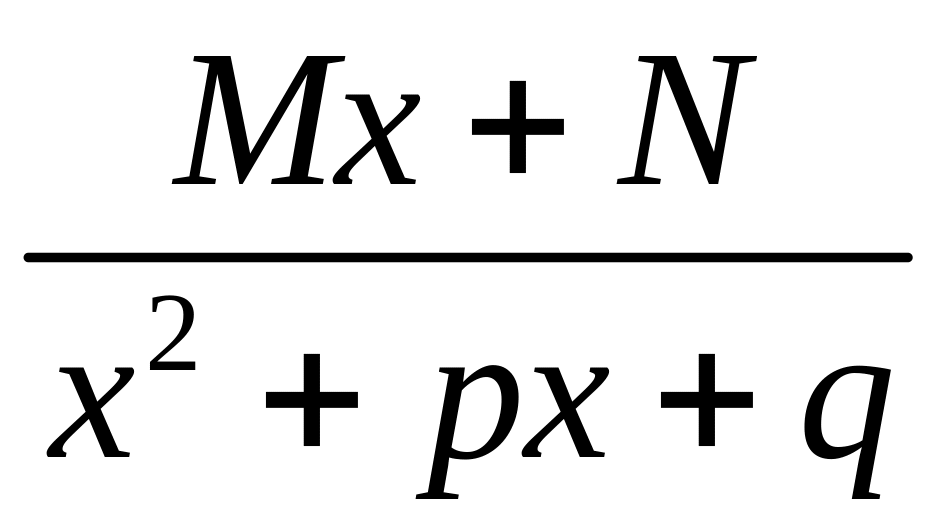(корни знаменателя комплексные, т.е. );

(IV) 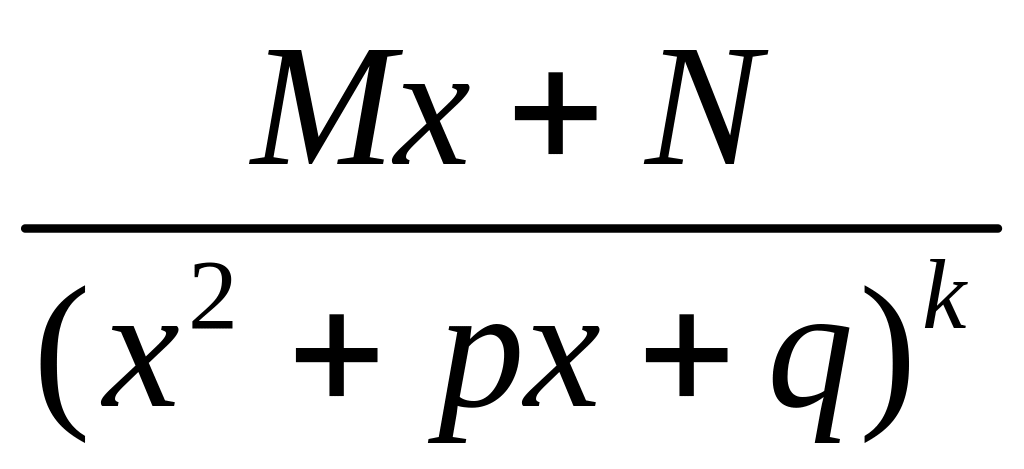( , корни знаменателя комплексные);

где  действительные числа, называются простейшими рациональными дробями I, II, III и IV типов.

Сформулируем теорему без доказательства о разложении правильной дроби в сумму простейших дробей.

Теорема 1.2 (о разложении правильной дроби в сумму простейших дробей).

Всякую правильную дробь , знаменатель которой разложен на множители

,

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

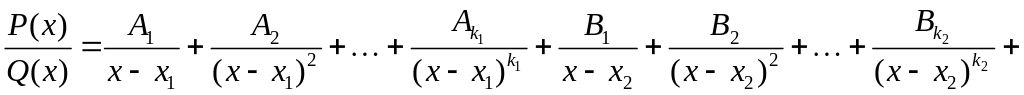
(1.4)

,

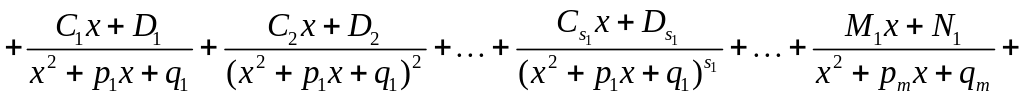
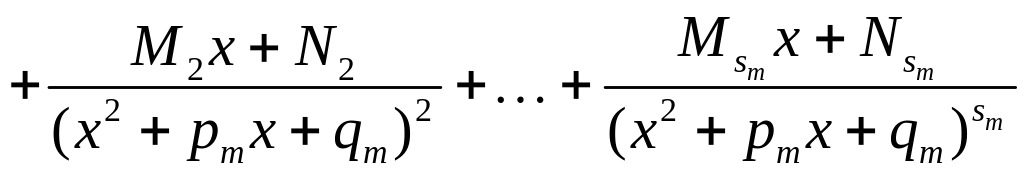где  некоторые действительные коэффициенты.

Например, .

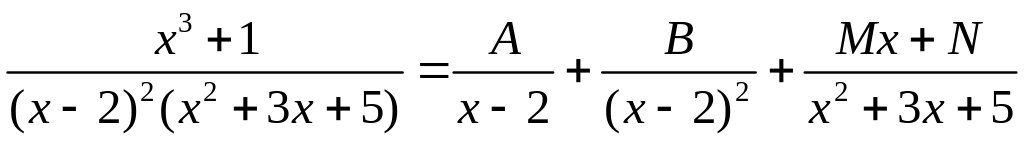Для нахождения коэффициентов в равенстве (1.4) можно применить метод неопределенных коэффициентов. Суть метода такова:

1) В правой части равенства (1.4) приводим к общему знаменателю сумму простейших дробей. В результате получаем тождество 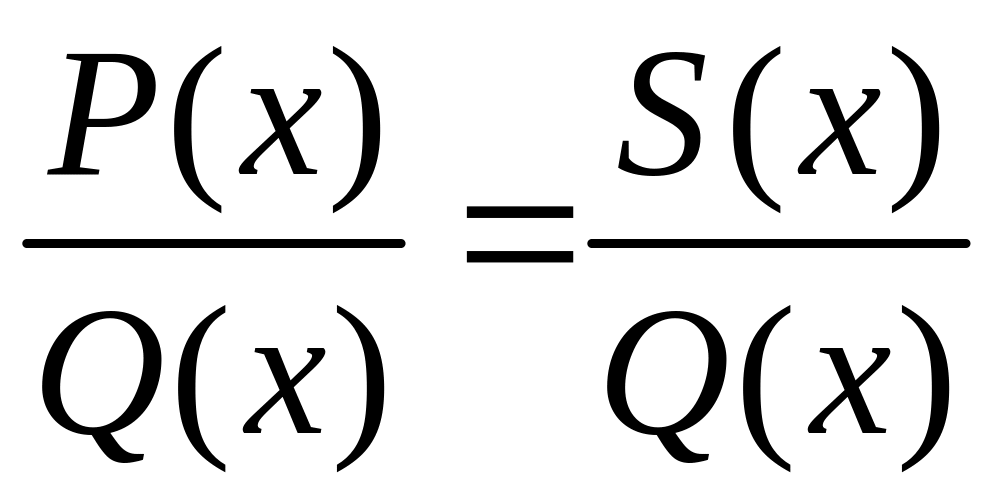, где  многочлен с неопределенными коэффициентами.

2) Так как в полученном тождестве знаменатели равны, то тождественно равны и числители, т.е.

.

3) Приравнивая коэффициенты при одинаковых степенях в обеих частях тождества, получаем систему уравнений, из которой и определяем искомые коэффициенты.

1.8. Интегрирование рациональных дробей

Выше были введены четыре типа простейших дробей. Найдем интегралы от простейших дробей.

(I) .

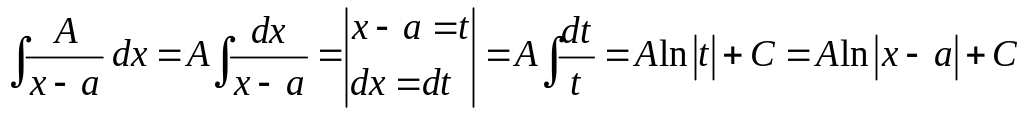(II) .

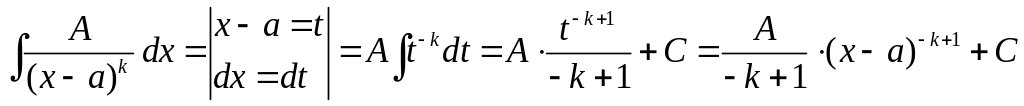Пример 1.6. Найти интеграл .

Решение.



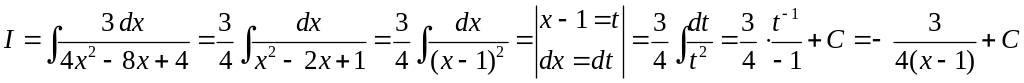
(III) Рассмотрим интеграл

.

.

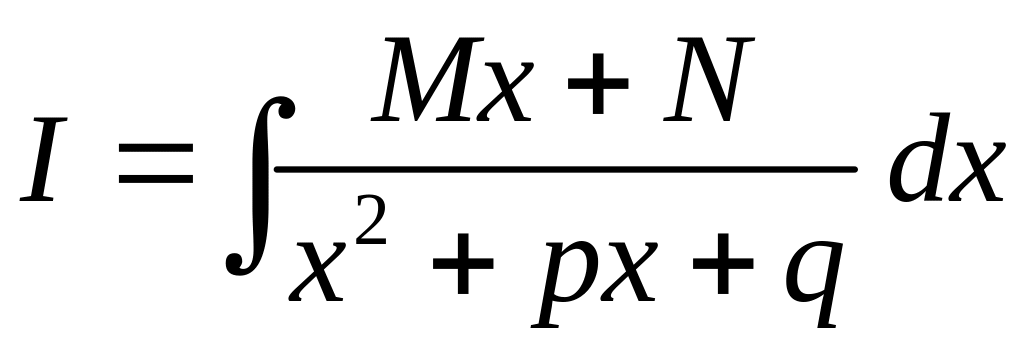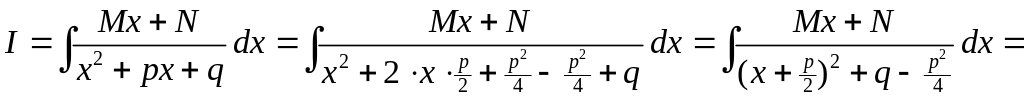
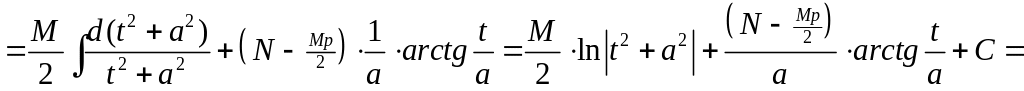
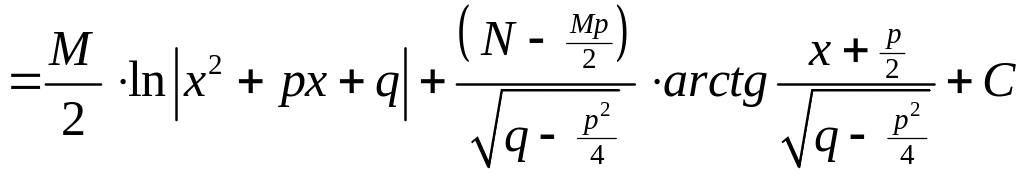Пример 1.7. Найти интеграл .

Решение.

.



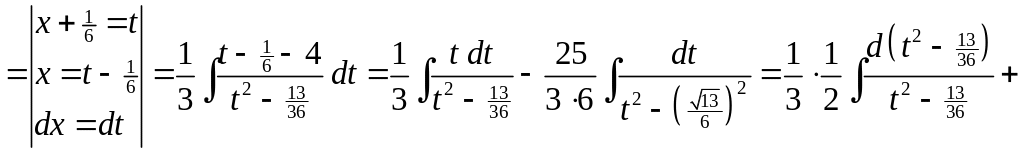
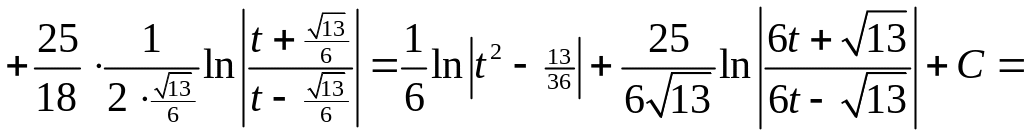
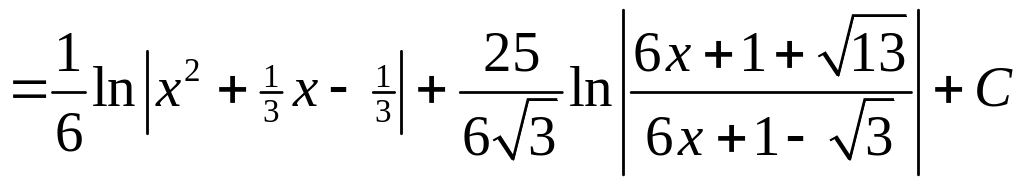(IV) Интеграла типа 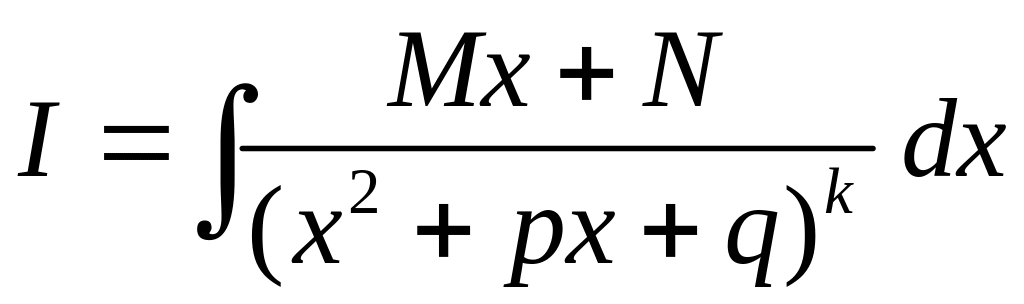рассматривать не будем.

Для интегрирования рациональных дробей сформулируем общее правило.

1. Если дробь неправильная, то представить ее в виде суммы многочлена и правильной дроби.

2. Разложив знаменатель правильной дроби на множители, представить ее в виде суммы простейших рациональных дробей.

3. Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример 1.8. Найти интеграл .

Решение.

.

Методом неопределенных коэффициентов найдем .

;

;

.

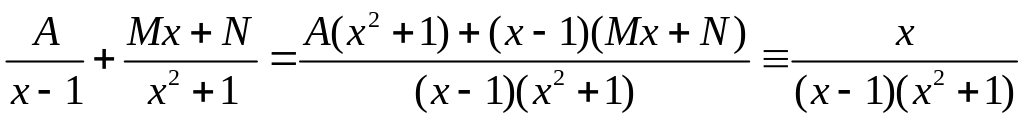Составляем и решаем систему линейных уравнений:

   .

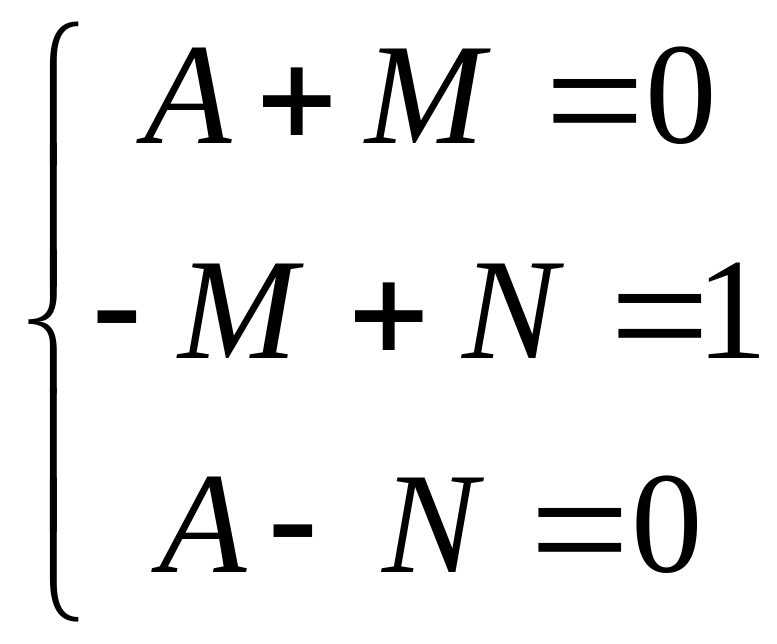
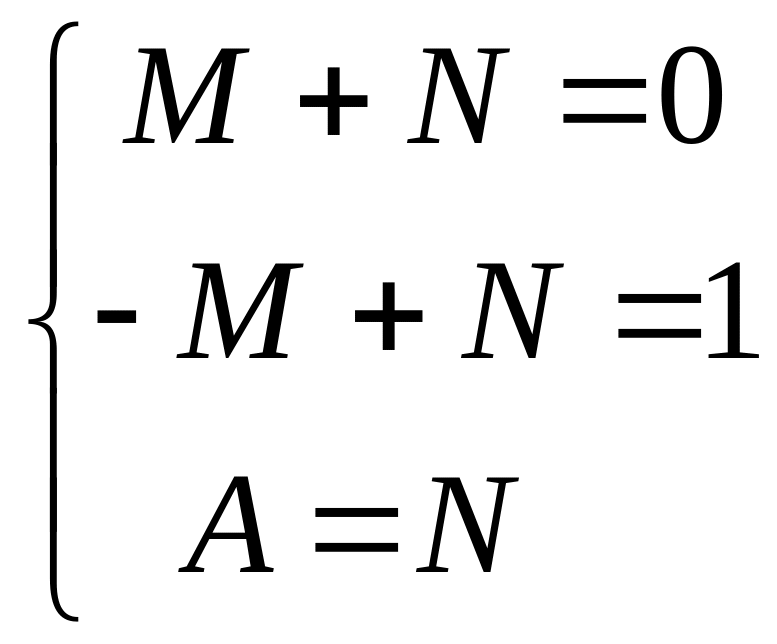
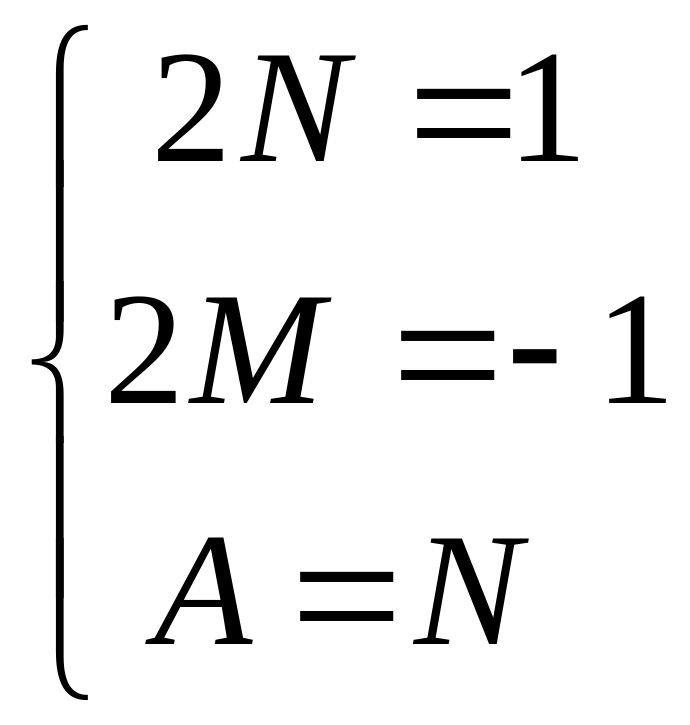
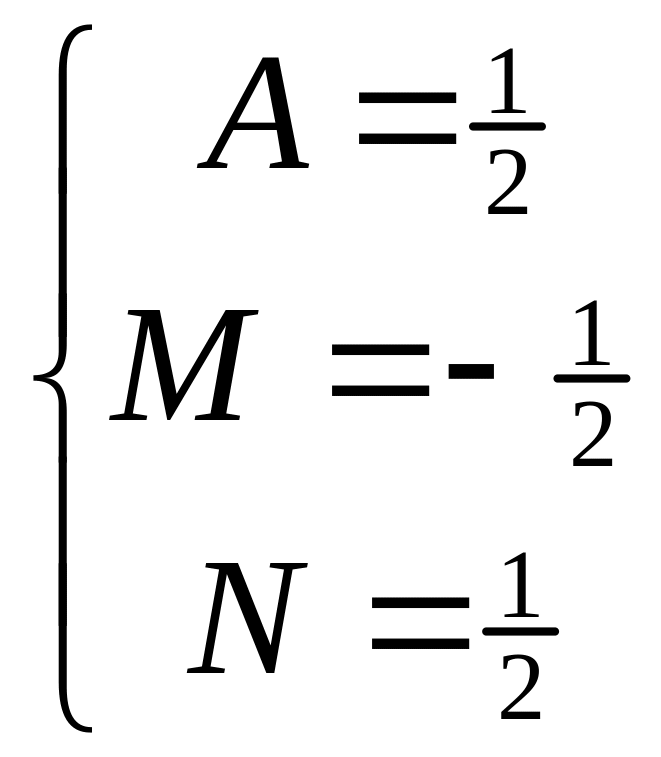Далее находим интеграл:

.


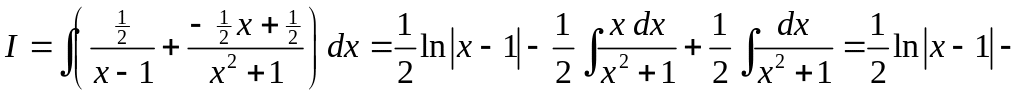