Раздел 1
ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ (ФНП)
1. Функция двух переменных
1.1. Основные понятия
Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.
Например, площадь
прямоугольника есть функция двух
независимо друг от друга изменяющихся
переменных – длин сторон прямоугольника
и
,
которая выражается формулой:
.
Например, функция
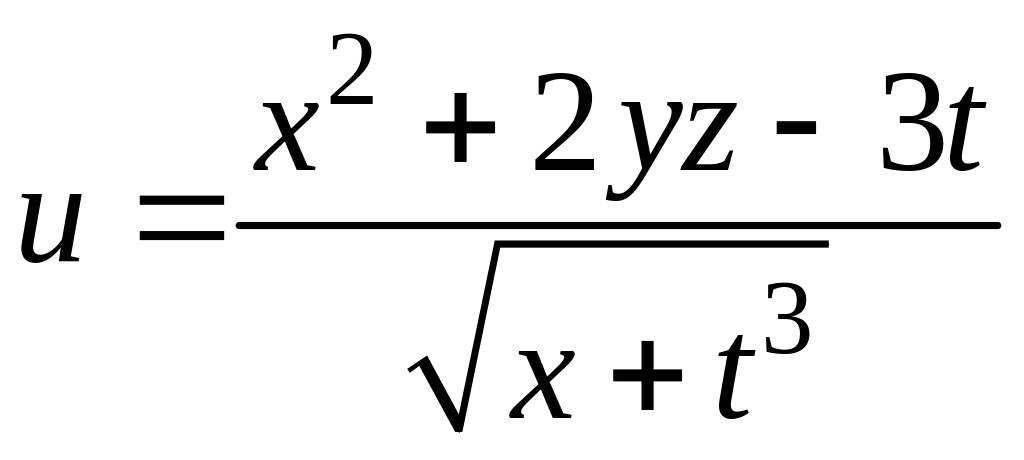
есть функция от четырех переменных
и
.
Остановимся на случае двух переменных, которые будем обозначать и .
Каждой паре значений
и
соответствует точка на плоскости
,
координатами которой они служат.
Рассмотрим некоторое множество точек
на плоскости
и обозначим его через
,
т.е.
.
Надо отметить, что переменные
и
не зависимы друг от друга.
Определение 1.1. Если каждой паре
из некоторой области их изменения
,
поставлено в соответствие определенное
значение величины
,
то говорят, что
есть функция двух независимых
переменных
и
.
Записывается
.
При этом и называются независимыми переменными (аргументами), а зависимой переменной (функцией).
Множество пар
значений
и
,
при которых определена функция
,
называется областью определения
функции, обозначается
.
Если каждую пару значений
и
можно изобразить точкой на плоскости
,
то область определения функции
изобразиться в виде некоторой совокупности
точек этой плоскости. В частности,
область определения может быть вся
плоскость или ее часть, ограниченная
некоторыми линиями. Линию, ограничивающую
область, называют границей области.
Точки области, не лежащие на границе,
называются внутренними. Область,
состоящая из одних внутренних точек,
называется открытой. Область с
присоединенной к ней границей называется
замкнутой.
Пример 1.1. Найти область определения функции
.
Решение. Областью определения данной функции является множество точек плоскости , которые удовлетворяют решению системе неравенств
.
Определение функции двух переменных легко обобщить на случай трех или более переменных.
Определение 1.2. Если каждой
рассматриваемой совокупности значений
переменных
соответствует определенной значение
переменной
,
то
называют функцией независимых
переменных
и записывают
.
Так же как и для функции двух переменных,
можно говорить об области определения
функции трех, четырех и более переменных.
Так, например, для функции трех переменных
областью определения является некоторая
совокупность троек чисел
,
которые представляют совокупность
точек пространства. Область определения
функции четырех и более числа переменных
уже не допускает простого геометрического
истолкования.
Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графически.
Рассмотрим функцию
,
определенную в области
на плоскости
,
и систему прямоугольных декартовых
координат
.
В каждой точке
двух переменных. Из курса аналитической геометрии известно, что уравнение в пространстве определяет некоторую поверхность. Таким образом, графиком функции двух переменных является поверхность, проектирующаяся на плоскость в область определения функции. Каждый перпендикуляр к плоскости пересекает поверхность не более чем в одной точке.