21 Компенсация систематической погрешности в процессе измерения

В практике измерений применяется несколько методов, позволяющих за счет некоторого усложнения процедуры измерений получить результат измерения свободным от систематической погрешности. К ним относятся метод замещения, метод противопоставления и метод компенсации погрешности по знаку. 6.2.1 Метод замещения

Этот метод дает наиболее полное решение задачи компенсации постоянной систематической погрешности и представляет собой разновидность метода сравнения. Сравнение производится путем замены измеряемой величины известной величиной и так, чтобы воздействием известной величины привести средство измерения в то состояние, которое оно имело при воздействии измеряемой величины. 6.2.2 Метод противопоставления

При взвешивании на рычажных весах условие равновесия весов равенство произведений массы на длину плеча весов. Если длины плеч одинаковы, то масса груза и гирь одинаковы. Если длины плеч различны (из-за технологического разброса длин плеч при их изготовлении, например), то при взвешивании каждый раз возникает систематическая погрешность.

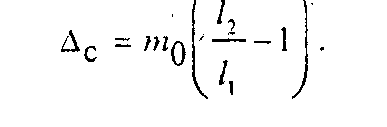Для исключения этой погрешности взвешивание производится в два этапа. Сначала взвешивают груз уравновешивая весы гирями (Мо1). Затем взвешиваемый груз перемещают на ту чашу весов, где прежде были гири и вновь уравновешивают весы (новой массой гирь Мо2)). Теперь исключив из полученных равенств отношение плеч, найдем

Как видно из формулы, длины плеч не входят в окончательный результат взвешивания. 6.2.3 Метод компенсации погрешности по знаку Этот метод также предусматривает проведение измерения в два этапа выполняемых так, чтобы постоянная систематическая погрешность входила в показания средства измерения на каждом этапе с разными знаками. За результат измерения принимают полусумму показаний — систематические погрешности при этом взаимно компенсируются.

6.2.4 Суммирование систематических погрешностей Независимо от того, к какому виду относится измерение, является ли оно прямым, косвенным совместным или совокупным, систематическая погрешность результата; измерения оценивается, как правило, по ее известным составляющим.Поскольку в каждом конкретном случае каждая систематическая составляющая получает конкретную реализацию (она либо постоянная, либо известен закон ее изменения), то результирующая, суммарная систематическая погрешность представляет собой алгебраическую сумму составляющих:

22 Вероятностное описание результатов и погрешностей

Когда при проведении с одинаковой тщательностью и в одинаковых условиях повторных наблюдений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Каждая такая погрешность возникает вследствие одновременного воздействия на результат наблюдения многих случайных возмущений, и сама является случайной величиной. В этом случае предсказать результат отдельного наблюдения и исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов наблюдений от Хmin до Хmax, где Хmin и Хmax — соответственно, нижняя и верхняя границы разброса. Методы теории вероятностей, математической статистики позволяют установить вероятностные (статистические) закономерности появления случайных погрешностей и на основании этих закономерностей дать количественные оценки результата измерения и его случайной погрешности.

Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма — закон распределения плотности вероятностей случайной величины.

Если распределение случайной величины х статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины, в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Это означает, что единожды построив гистограмму, при последующих сериях наблюдений можно с определенной долей уверенности заранее предсказать распределение результатов наблюдений по интервалам. При бесконечном увеличении числа наблюдений n  и бесконечном уменьшении ширины интервалов l  ступенчатая кривая, огибующая гистограмму, перейдет в плавную кривую f(х) (рис.), называемую кривой плотности распределения вероятностей случайной величины, а уравнение, описывающее ее, — дифференциальным законом распределения. Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде:

неопределенный интеграл от f(х) по dx равен 1.

Закон распределения дает полную формацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения случайной величины f(х), то вероятность Р ее попадания в интервал от Х₁, до Х₂ равна интегралу Х₁, - Х₂ от f(х) по dx .

Графически эта вероятность выражается отношением площади, лежащей под кривой f(х) в интервале от Х₁, до Х₂ к общей площади, ограниченной кривой распределения.

Кроме непрерывных случайных величин в метрологической практике встречаются и дискретные случайные величины.

Для описания частных свойств случайной величины используют числовые характеристики распределений. В качестве числовых характеристик выступают моменты случайных величин: начальные и центральные. Все они представляют собой некоторые средние значения; причем, если усредняются величины, считываемые от начала координат, моменты называются начальными, а если от центра закона распределения — то центральными. Начальный момент k-го порядка определяется формулами

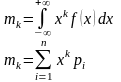
где p_i— вероятность появления дискретной величины.

Здесь и ниже первая формула относится к непрерывным, а вторая к дискретным случайным величинам. Из начальных моментов наибольший интерес представляет математическое ожидание случайной величины (к = 1),

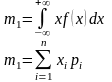
Центральные моменты к-го порядка рассчитываются по формулам

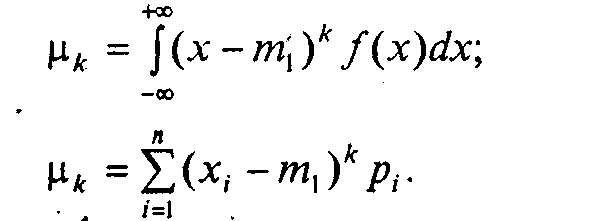
Из центральных моментов особенно важную роль играет второй момент (к = 2), дисперсия случайной величины D

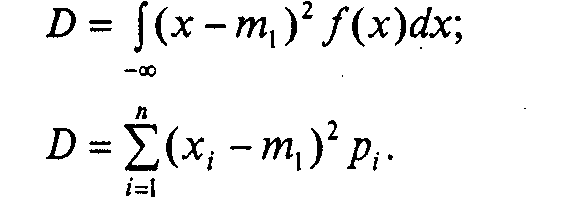
Дисперсия случайной величины характеризует рассеяние отдельных значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии — средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.